Systems theory and complexity: Part 1
Kurt A. Richardson
Introduction
The motivation for this multi-part series is solely my observation that much of the writing on complexity theory seems to have arbitrarily ignored the vast systems theory literature. I don’t know whether this omission is deliberate (i.e., motivated by the political need to differentiate and promote one set of topical boundaries from another; a situation unfortunately driven by a reductionist funding process) or simply the result of ignorance. Indeed, Phelan (1999) readily admits that he was “both surprised and embarrassed to find such an extensive body of literature [referring to systems theory] virtually unacknowledged in the complexity literature.” I am going to assume the best of the complexity community and suggest that the reason systems theory seems to have been forgotten is ignorance, and I hope this, and subsequent, articles will familiarize complexity thinkers with some aspects of systems theory; enough to demonstrate a legitimate need to pay more attention to this particular community and its associated body of literature. The upcoming 11th Annual ANZSYS Conference/Managing the Complex V Systems Thinking and Complexity Science: Insights for Action (a calling notice for which can be found in the “Event Notices” section of this issue) is a deliberate attempt to forge a more open and collaborative relationship between systems and complexity theorists.
There are undoubtedly differences between the two communities, some of which are analyzed by Phelan (1999). Six years on from Phelan’s article, I find that some of the differences he discusses have dissolved somewhat, if not entirely. For example, he proposes that systems theory is preoccupied with “problem solving” or confirmatory analysis and has a critical interpretivist bent to it, whereas complexity theory is exploratory and positivist. Given the explosion in the management science literature concerning the application of complexity to organizational management I would argue that the complexity community as a whole is rather more inclined to confirmatory analysis than it might have been in 1999. I think that part of Phelan’s assessment that complexity theory is positivist comes from his characterization of complexity as a preoccupation with agent-based modelling. Again, this may well have been an accurate assessment in 1999, but I find the assessment a little too forced for 2005. See for example Cilliers (1998) and Richardson (2004a) for views of complexity that explore the limitations of a positivist-only view of complexity. Also, refer to Goldstein’s introduction “Why complexity and epistemology?” in this issue for reasons as to why a purely positivistic characterization of complexity theory is no longer appropriate. I think it is still valid to suggest that there are philosophical and methodological differences between the systems and complexity communities, although, if one looks hard enough there is sufficient diversity within the communities themselves to undermine such simplistic characterizations in the first place.
Of course there are differences between systems theory and complexity theory, but there are also many similarities. For example, most, if not all, the principles/laws of systems theory are valid for complex systems. Given the seeming lack of communication between complexity and systems theorists this seriesof articles will focus on the overlaps. The first few articles will review some general systems laws and principles in terms of complexity. The source of the laws and principles of general systems theory are taken solely from Skyttner’s General Systems Theory: Ideas and Applications, which was recently republished (Skyttner, 2001).
The second law of thermodynamics
he second law of thermodynamics is probably one of the most important scientific laws of modern times. The ‘2nd Law’ was formulated after nineteenth century engineers noticed that heat cannot pass from a colder body to a warmer body by itself. According to philosopher of science Thomas Kuhn (1978: 13), the 2nd Law was first put into words by two scientists, Rudolph Clausius and William Thomson (Lord Kelvin), using different examples, in 1850-51. Physicist Richard P. Feynman (Feynman et al., 1963: section 44-3), however, argued that the French physicist Sadi Carnot discovered the 2nd Law 25 years earlier - which would have been before the 1st Law (conservation of energy) was discovered!
Simply stated the 2nd Law says that in any closed system the amount of order can never increase, only decrease over time. Another way of saying this is that entropy always increases. The reason this law is an important one to discuss in terms of complexity theory is that it is often suggested that life itself contradicts this law. In more familiar terms - to complexologists at least - the phenomena of self-organization, in which order supposedly emerges from disorder, completely goes against the 2nd Law.
There are several reasons why this assertion is incorrect. Firstly, the 2nd Law is concerned with closed systems and nearly all the systems of interest to complexity thinkers are open; so why would we expect the 2nd Law to apply? What if we consider the only completely closed system that we know of: the Universe? Even if it is True that the entropy of the Universe always increases this still does not deny the possibility of local entropy decrease. To understand why this is the case we need to understand the nature of the 2nd Law itself (and all scientific laws for that matter). The 2nd Law is a statistical law. This means it should really be read as on average, or on the whole, the entropy of closed systems will always increase. The measure of disorder, or entropy, is a macroscopic measure and so is the average over the whole system. As such there can be localized regions within the system itself in which order is created, or entropy decreases, even while the overall average is increasing. Another way to say this is that microlevel contradictions to macrolevel laws do not necessarily invalidate macrolevel laws. The 2nd Law and the self-organizing systems principle (which will be covered in a later installment) operate in different contexts and have different jurisdictions.
Despite the shortcomings of applying the 2nd Law to complex systems, there are situations in which it is still perfectly valid. Sub-domains, or subsystems, can emerge locally within a complex system that are so stable that, for a period, they behave as if they were closed. Such domains are critically organized, and as such that they could qualitatively evolve rather rapidly. However, during their stable periods it is quite possible that the 2nd Law is valid, even if only temporarily and locally.
The complementary law
The complementary law (Weinberg, 1975) suggests that any two different perspectives (or models) about a system will reveal truths regarding that system that are neither entirely independent nor entirely compatible. More recently, this has been stated as: a complex system is a system that has two or more non-overlapping descriptions (Cohen, 2002). I would go as far as to include “potentially contradictory” suggesting that for complex systems (by which I really mean any part of reality I care to examine) there exists an infinitude of equally valid, non-overlapping, potentially contradictory descriptions. Maxwell (2000) in his analysis of a new conception of science asserts that:
“Any scientific theory, however well it has been verified empirically, will always have infinitely many rival theories that fit the available evidence just as well but that make different predictions, in an arbitrary way, for yet unobserved phenomena.” (Maxwell, 2000).
In Richardson (2003) I explore exactly this line of thinking in my critique of bottom-up computer simulations.
The complementary law also underpins calls in some complexity literature for philosophical/epistemological/methodological/theoretical pluralism in complexity thinking. What is interesting here is how the same (or at least very similar) laws/principles have been found despite the quite different routes that have been taken - a process systems theorists call equifinality. This is true for many of the systems laws I will discuss here and in future installments.
System holism principle
The system holism principle is probably the most well known principle in both systems and complexity communities, and is likely the only one widely known by ‘outsiders’. It has it roots in the time of Aristotle and simply stated it says “the whole is greater than the sum of its parts”. More formally: “a system has holistic properties not manifested by any of its parts and their interactions. The parts have properties not manifested by the system as a whole” (Skyttner, 2001: 92). This is one of most interesting aspects of complex systems: that microlevel behavior can lead to macrolevel behavior that cannot be easily (if at all) derived from the microlevel from which it emerged. In terms of complexity language we might re-label the system holism principle as the principle of vertical emergence. (N.B. Sulis, in this issue, differentiates between vertical and horizontal emergence).
The wording: “the whole is greater than the sum of its parts” is problematic to say the least. To begin with the use of the term “greater than” would suggest that there is some common measure to compare the whole and its parts and that by this measure the whole is greater than the sum of those parts. I think this wrong. An important property of emergent wholes is that they cannot be reduced to their parts (a reversal of the system holism principle), i.e., wholes are qualitatively different from their parts (other than they can be recognized as coherent objects) - they require a different language to discuss them. So, in this sense, wholes and their component parts are incommensurable - they cannot be meaningfully compared - they are different! Of course, if mathematicians do find a way to bootstrap (without approximation) from micro to macro - a step that is currently regarded by many as intractable - then maybe a common (commensurable) measure can be applied. What we really should say is “the whole is different from the sum of its parts and their interactions”.
The issue of commensurability is an interesting one and crops up time and time again in complexity thinking. Indeed, it was the focus of a recent ISCE conference held in Washington (September 18-19, 2004). One way to make the incommensurable commensurable is to abstract/transform the incommensurable entities in a way that allow comparison. As long as we remember that it is the transformed entities that are being compared and not the entities themselves (as abstraction/transformation is rarely a conservative process) then useful comparisons can indeed be made.
One last issue with the system holism principle: the expression “the whole is greater than the sum of its parts” implies that, although the problem of intractability prevents us from deriving wholes from parts, in principle the whole does emerge from those parts (and their interactions) only, i.e., the parts are enough to account for the whole even if we aren’t able to do the bootstrapping itself. In Richardson (2004b) the problematic nature of recognizing emergent products is given as a reason to undermine this possibility. In that paper, it is argued that the recognition of wholes as wholes is the result of applying a particular filter. Filters remove information and so the resulting wholes are what is left after much of reality has been filtered out - oddly enough, what remains after the filtering process is what is often referred to as ‘reality’. So, molecules do not emerge from atoms, as atoms are only an idealized representation of that level of reality (a level which is determined by the filter applied) and as idealizations are not sufficient in themselves to account for the properties of molecules (which represent another idealization). An implication of this is that there exists chemistry that cannot be explained in terms of physics - this upsets of whole unification-of-the-sciences program. Only in idealized abstractions can we assume that the parts sufficiently account for the whole.
Darkness principle
In complexity thinking the darkness principle is covered by the concept of incompressibility. The darkness principle says that “no system can be known completely” (Skyttner, 2001: 93). The concept of incompressibility suggests that the best representation of a complex system is the system itself and that any representation other than the system itself will necessarily misrepresent certain aspects of the original system. This is a direct consequence of the nonlinearity inherent in complex systems. Except in very rare circumstances nonlinearity is irreducible (although localized linearization techniques, i.e., assuming linearity locally, do prove useful).
There is another source of ‘darkness’ in complexity theory as reported by Cilliers (1998: 4-5):
“Each element in the system is ignorant of the behavior of the system as a whole, it responds only to information that is available to it locally. This point is vitally important. If each element ‘knew’ what was happening to the system as a whole, all of the complexity would have to be present in that element.” (original emphasis).
So, there is no way a member of a complex system can ever know it completely - we will always be in the shadow of the whole.
Lastly there is the obvious point that all complex systems are by definition open and so it is nigh on impossible to know how the system’s environment will affect the system itself - we simply cannot model the world, the Universe and everything.
Eighty-twenty principle
The eighty-twenty principle has been used in the past to justify the removal of a large chunk of an organization’s resources, principally its workforce. According to this principle, in any large, complex system, eighty per cent of the output will be produced by only twenty per cent of the system. Recent studies in Boolean networks, a particularly simple form of complex system, have shown that not all members of the network contribute to the function of the network as a whole. The function of a particular Boolean network is related to the structure of its phase space, particularly the number of attractors in phase space. For example, if a Boolean network is used to represent a particular genetic regulatory network (as in the work of Kauffman, 1993) then each attractor in phase space supposedly represents a particular cell type that is coded into that particular genetic network. It has been noticed that the key to the stability of these networks is the emergence of stable nodes, i.e., nodes whose state quickly freezes. These nodes, as well as others called leaf nodes (nodes that do not input into any other nodes), contribute nothing to the asymptotic (long-term) behavior of these networks. What this means is that only a proportion of a dynamical network’s nodes contribute to the long-term behavior of the network. We can actually remove these stable/ frozen nodes (and leaf nodes) from the description of the network without changing the number and period of attractors in phase space, i.e., the network’s function. Figure 1 illustrates this. The network in Figure 1b is the reduced version of the network depicted in Figure 1a. I won’t go into technical detail here about the construction of Boolean networks, please feel free to contact me directly for further details. Suffice to say, by the way I have defined functionality, the two networks shown in Figure 1 are functionally equivalent. It seems that not all nodes are relevant. But how many nodes are irrelevant?
Figure 2 shows the frequency of different sizes of reduced network. The experiment performed was to construct a large number (100,000) of random Boolean networks containing only ten nodes, each having a random rule (or transition function) associated with it, and two randomly selected inputs. Each network is then reduced so that the resulting network only contains relevant nodes. Networks of different sizes resulted and their proportion to the total number of networks tested was plotted. If we take an average of all the networks we find that typically only 60% of all nodes are relevant. This would suggest a one hundred - sixty principle (as 100% of functionality is provided by 60% of the network’s nodes), but it should be noted that this ratio is not fixed for networks of all types - it is not universal. This is clearly quantitatively different from the eighty-twenty ratio but still implies that a good proportion of nodes are irrelevant on average. What do these so-called irrelevant nodes contribute? Can we really just remove them with no detrimental consequences? A recent study by Bilke and Sjunnesson (2001) showed that these supposedly irrelevant nodes do indeed play an important role.
One of the important features of Boolean networks is their intrinsic stability, i.e., if the state of one node is changed/perturbed it is unlikely that the network trajectory will be pushed into a different attractor basin. Bilke and Sjunnesson (2001) showed that the reason for this is the existence of the, what we have called thus far, irrelevant nodes. These ‘frozen’ nodes form a stable core through which the perturbed signal is dissipated, and therefore has no long term impact on the network’s dynamical behavior. In networks for which all the frozen nodes have been removed, and only relevant nodes remain, it was found that they were very unstable indeed - the slightest perturbation would nudge them into a different basin of attraction, i.e., a small nudge was sufficient to qualitatively change the network’s behavior. As an example, the stability (or robustness) of the network in Figure 1a is 0.689 whereas the stability of its reduced, although functionally equivalent network, is 0.619 (N.B. The robustness measure is an average probability measure indicating the chances that the system will move into a different attractor basin if a single bit of one node, selected at random, is perturbed. The measure ranges from 0 to 1 where 1 represents the most stable. The difference in robustness for the example given is not that great, but the difference does tend to grow with network size - we have considered networks containing only ten nodes here).
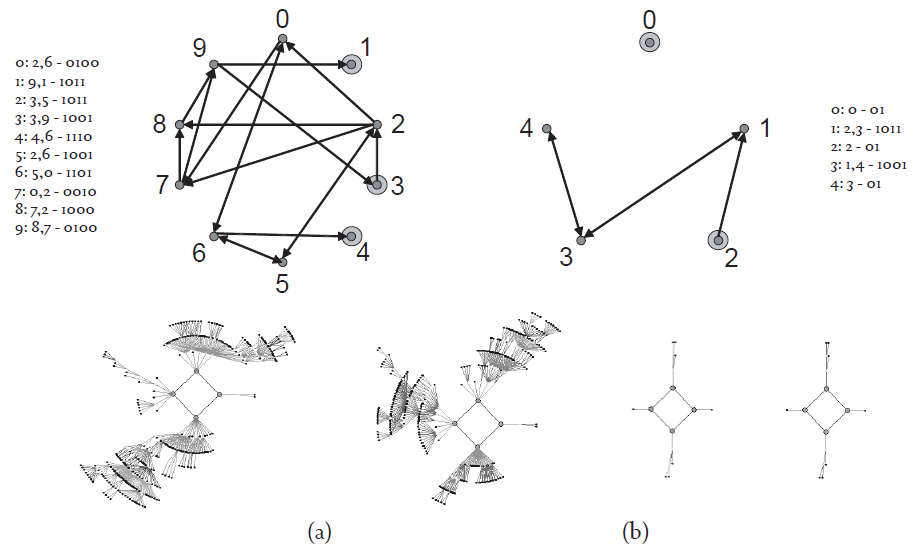
Figure 1 An example of (a) a Boolean network, and (b) its reduced form. The nodes which are made up of two discs feedback onto themselves. The connectivity and transition function lists at the side of each network representation are included for those readers familiar with Boolean networks. The graphics below each network representation show the attractor basins for each network. The phase space of both networks contain two period-4 attractors, although it is clear that the basin sizes (i.e., the number of states they each contain) are quite different.
Prigogine said that self-organization requires a container (self-contained-organization). The stable nodes function as the environmental equivalent of a container, and indeed one of the complex systems notions not found in systems theory is that environmental embodiments of weak signals might matter.
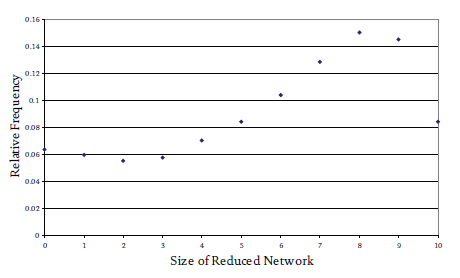
Figure 2 The relative frequency distribution of reduced network sizes
So it seems that, although many nodes do not contribute to the long term behavior of a particular network, these same nodes play a central role as far as network stability is concerned. Any management team tempted to remove 80% of their organization in the hope of still achieving 80% of their yearly profits, would find that they had created an organization that had no protection whatsoever to even the smallest perturbation from its environment - it would literally be impossible to have a stable business.
Summing up
As mentioned in the opening paragraphs of this article, my aim in writing this series is to encourage a degree of awareness with general systems ideas that is currently not exhibited in the ‘official’ complexity literature. In each installment I will explore a selection of general systems laws and principles in terms of complexity science. When this task has been completed we might begin to develop a clearer understanding of the deep connections between systems theory and complexity theory and then make a concerted effort to build more bridges between the two supporting communities - there are differences but not as many as we might think.
References
Bilke, S. and Sjunnesson, F. (2001). “Stability of the Kauffman model,” Physical Review E, 65: 016129-1.
Cilliers, P.(1998).Complexity and post modernism: Understand complex systems, NY: Routledge.
Cohen, J. (2002). Posting to the Complex-M listserv, 2nd September.
Feynman, R. P, Leighton, R. B. and Sands, M. (1963), The Feynman lectures on physics: Volume 1, Reading, MA: Addison-Wesley Publishing Company.
Kauffman, S. (1993). The origins of order: Self-organization and selection in evolution, New York, NY: Oxford University Press.
Kuhn, T. (1978), Black-body theory and the quantum discontinuity, 1894-1912, The University of Chicago Press.
Maxwell, N. (2000). “A new conception of science,” Physics World, August: 17-18.
Phelan, S. E. (1999). “A note on the correspondence between complexity and systems theory,” Systemic Practice and Action Research, 12(3): 237-2 46.
Richardson, K. A. (2003). “On the limits of bottom-up computer simulation: Towards a nonlinear modeling culture,” Proceedings of the 36th Hawaiian international conference on system sciences, Jan 7th-10th, IEEE: California.
Richardson, K. A. (2004a). “ The problematization of existence: Towards a philosophy of complexity,” Nonlinear Dynamics, Psychology, and Life Science, 8(1): 17-40.
Richardson, K. A. (2004b). “On the relativity of recognizing the products of emergence and the nature of physical hierarchy,” Proceedings of the 2nd Biennial International Seminar on the Philosophical, Epistemological and Methodological Implications of Complexity Theory, January 7th-10th, Havana International Conference Center, Cuba.
Skyttner, L. (2001). General systems theory: Ideas and applications, NJ: World Scientific.
Weinberg, G. (1975). An Introduction to general systems thinking, New York, NY: John Wiley.