The hegemony of the physical sciences:
An exploration in complexity thinking

Kurt Richardson¹

Institute for the Study of Coherence and Emergence, 395 Central Street, Mansfield, MA 02048, USA

Abstract: Traditionally the natural sciences, particularly physics, have been regarded as the Gatekeepers of Truth. As such the legitimacy of others forms of knowledge have been called into question, particularly those methods that characterize the ‘softer’ sciences, and even the arts. This paper begins with an extended discussion concerning the main features of a complex system, and the nature of the boundaries that emerge within such systems. Subsequent to this discussion, and by assuming that the Universe at some level can be well-described as a complex system, the paper explores the notion of ontology, or existence, from a complex systems perspective. It is argued that none of the traditional objects of science, or any objects from any discipline, formal or not, can be said to be real in any absolute sense although a substantial realism may be temporarily associated with them. The limitations of the natural sciences is discussed as well as the deep connection between the ‘hard’ and the ‘soft’ sciences. As a result of this complex systems analysis, an evolutionary philosophy referred to as quasi-‘critical pluralism’ is outlined, which is more sensitive to the demands of complexity than contemporary reductionistic approaches.

“No human being will ever know the Truth, for even if they happened to say it by chance, they would not know they had done so.” Xenophanes

“If you see things as they are here and now, you have seen everything that has happened from all eternity. All things are an interrelated Oneness.” Marcus Aurelius

Introduction

Realism versus constructivism

There are at least two broad perspectives from which the status of our scientific knowledge claims can be understood. The first is a purely realist view of scientific knowledge, referred to as scientific realism. According to this view the “theoretical entities that are characterized by a true theory actually exist even though they cannot be directly observed. Alternatively, that the evidence that confirms a theory also serves to confirm the existence of any theoretical or ‘hypothetical’ entities characterized by that theory” (Fetzer and Almeder [17: 118]). This definition suggests that scientific knowledge gives us direct knowledge of entities that exist independent of the existence of any observer, i.e., rigorous application of scientific methods yields theories of certain entities that exist mind-independently (independently of what we believe or feel about those entities). In this view an objective reality does exist, and that it is through the application of method that we can have objective scientific knowledge of ‘reality’. In complete opposition to the realist position is idealism. This position argues that, though there does exist an objective reality, we can never have direct objective knowledge concerning that reality. Accordingly, knowledge is manufactured rather than discovered. The manufacturing process is inherently biased by our methods of production and is incapable of delivering objective knowledge of some external reality: objectivity becomes no more than a myth. Social constructivism, which is a form of idealism, in its extreme form regards scientific knowledge as merely a socially-constructed discourse that is inherently subjective in nature. As there can be no objective knowledge, there can be no dominant discourse because there can be no test or argument that could conclusively support the dominance of one discourse over another. As such, science is just another approach ‘out there’ to making sense and should be treated with no more reverence than any other approach. As Masani [30] laments, “constructivism is anti-scientific to the bone.”

The relationship between language and objective reality

An alternative way to distinguish between realism and idealism is to consider the relationship between the language we use to describe reality and reality itself. Realists argue that there is a one-to-one correspondence between our language and reality. This leads to a number of interesting consequences like, for example, the belief that there is a best, or universal, language for describing reality and that that language happens to be the language of science, namely mathematics and logic. Idealists, specifically relativists, on the other hand argue that there is no relationship whatsoever between our language and reality. The terms or labels we use are no more than useful sense-making tools that, though convenient, have no intrinsic basis in some notional objective reality. Though I do not believe that anyone who supports either of these positions is naïve enough to believe in them wholeheartedly, this is generally how the debate between realism and idealism is set up. Physical scientists are criticized for their intellectual arrogance/imperialism, which is justified through strongly realist beliefs, and idealist critics are ridiculed for their apparently wild and poorly argued descriptions of what they think science actually is as well as their omission of reality in their theories.

The hegemony of the physical sciences

Primarily because of the success of science-driven technology, there is an enormous wealth of evidence that supports the privileging of scientific discourse over every other. This success has perhaps blinded us to the shortcomings of the scientific process and has lead to an unquestioned belief that because science has successfully explained so much it can probably explain everything. Every facet of human life can supposedly be productively examined through the eyes of science. This position is commonly referred to as scientism (though practical science—as opposed to some popularized caricature of science—is not synonymous with scientism). And, though indirect evidence of these shortcomings is becoming more widespread, putting the brakes on the train of scientism is no trivial undertaking. Often the failures of science, which are considerable when we consider social planning or environmental policy, are put down to the bad application of reductionist methods rather than seeing these failures as the result of applying reductionist methods to inappropriate subject matter.

Contrary to popular belief science is not capable of considering all phenomena. In fact, it is quite inflexible in its requirements. The principal requirement that will be considered herein is that scientific methods require that the object of interest is stable, i.e., the boundaries (or, patterns) that delimit the object from the ‘background’ (the objects complement) must be stable and assumed to be real. This stability allows repetitive examinations to be undertaken that allow the knowledge concerning that object to be refined and tested so much so that our confidence in our knowledge of that object becomes so great that we might begin to unquestionably assume that we have an accurate description to hand. In a more generic way, what I am saying is that scientific knowledge can only be obtained for contexts which are incredibly stable. This approach yields a tremendous amount of understanding that can be turned to the development of cars, computers, building methods, etc.—just about anything that can be constructed from parts that behave qualitatively in much the same way whatever context they are placed within. What about objects of interest that have far less rigid boundaries? Social systems, for example, change and evolve. The boundaries, or patterns, that describe such systems continuously change and emerge such that the extraction of uniformities is far from a trivial matter. By their very nature, the context changes and repetitive examinations are at worse impossible, and at best highly problematic. To apply reductionist science to such systems we have to fake stability. We are forced to reduce the system of interest to an idealized caricature that remains steady over time. Of course this is what we really do when we look at any system, be it an atom or an ecology, but for some reason our reductions seem to be more harmful when considering ecologies (i.e., complex systems) as the relationship between the description that would allow a scientific analysis and a notional ‘real’ description is gaping.

These cracks in the scientific façade have been made more apparent with our ability, supported through incredible growth in computer power (and, ironically, through the dogmatic application of reductionist science) to construct models of simple² complex systems. The emerging science of complexity forces us to revisit the nature of scientific knowledge and at the same time presents us with an alternative approach to understanding the limits of scientific methods. The interest for me personally is that, though many criticisms of science have been made by those whom the scientific community has regarded as outsiders and non-scientists, complexity science leads to a critique of science couched in the language of science itself. In a sense, the scientific language contains within it the seeds of its own limitations.

The aims and scope of this paper

The starting point for my discussion is to define what an abstract complex system is and then to assume that the Universe is well-described as a complex system at some arbitrarily deep level. From this starting point I will argue that no one discourse should unquestionably dominate all questions of knowledge, even though a purely realist foundation can still be sustained. The resulting philosophy may be called quasi-‘critical pluralism’. This position lies somewhere between the realist and idealist positions already discussed (despite its realist foundations), neither denying the potential of any particular perspective to yield useful understanding nor unquestionably privileging one select perspective over all others for all contexts. In some ways the resulting philosophy is quite empty. My hope is that quasi-critical pluralism will be seen as a natural conclusion from the realist assumptions of complexity. If, for example, postmodernist type arguments might be ‘derived’ scientifically then perhaps the current stalemate in the philosophy of science, fueled by a stubborn polarization between extremes, might be alleviated allowing an honest and humble exchange of ideas to occur.

In addition to this I had like to revisit arguments made in Richardson et al. [42] concerning the role incompressibility and system history play in the examination of complex systems, as my understanding of these topics has changed slightly. In some ways this could be seen as an unusual starting point as it assumes, like many of the writings on complexity, that the complex systems perspective, along with its associated set of tools, is legitimate. For example, it is often assumed that the complex adaptive system (CAS) view of organizations is the best. Often the justification for this assertion is the superficial similarities between the appearance of a real organization and an idealized CAS. So the paper begins with an exploration of complex systems in terms of their more common notions. However, the bulk of the second half of the paper discusses the legitimacy—or not—of utilizing any paradigm, let alone a complexity-based view (interestingly though, a complex systems view is employed to make this point). The paper could quite easily have begun in the middle with the discussion concerning the legitimacy of ontological shifts, and then moved on to discuss the details of the prevailing complex systems perspective.

What is a complex system?

A complex system is comprised of a large number of non-linearly interacting non-decomposable elements.

This is the simple definition of a complex system that is often given and is very similar to Langefors [28: 55] definition of a general system:

“A system is a set of entities with relations between them”

or, Van Gigch’s [50: 30] definition:

“A system is an assembly or set of related elements.”

If ‘non-linearly’ is inserted before ‘related elements’ then we end up with a very similar definition to the one given at the beginning of this section. As Backlund [3] has pointed out these sorts of definitions are incomplete. To ensure that the system we are interested in may not be simply reduced to two weakly interacting systems then we must also add that the systems’ components are connected in a way that prevents our system of interest being reduced to two or more distinct systems.

In addition to this particular shortcoming, the connectivity of the system must be such that the system displays behaviors associated with complex systems before it can be labelled as such. For example, as we shall discuss in the next section, complex systems display emergent properties, as there exists a non-trivial relationship between the system components and the system’s macroscopic properties. In my past endeavors to understand complex systems I have tried to develop, on a number of occasions, a typology that would clearly distinguish between complex and complicated systems; one that would hold up to scrutiny. One particular way of doing this is to regard complicated systems as much the same as complex systems except not having appropriate connectivity to display complex behaviors, such as emergence. However, when trying to conceive of a boundary between these two categories one quickly finds that it is very hard indeed, if not impossible, to develop a sound division that could be applied in all cases. What I quickly came to conclude was that the division between complicated and complex depended critically upon how the system was connected. Depending upon how the complicated system was put together, it may be that only a few new connections would be sufficient to transform it into a complex system, or, maybe a relatively large number of connections would be required to make the complicated system display emergence, for example. It should be noted that the complicated/complex distinction is not equivalent to the commonly used linear/non-linear distinction. Complicated systems may contain many non-linear interactions (e.g., computers are commonly regarding as examples of linear systems despite the fact that they comprise a vast number of non-linear responsive components such as transistors), they may even display limited non-linear behaviors. The key difference between the two is the absence of ‘novelty’ in complicated systems³. Complex systems can emerge into states that are not apparent from their constitution; in a sense new states are created⁴.

The principal difference between complicated and complex system is the presence of causal loops. For a system to be complex it must be connected in such a way that multiple causal loops are present that themselves interact with each other. So it is the qualitative design of the connectivity that allows, or not, complex behaviors. But again, the determination of a qualitative universal design process is problematic, and to my mind, an impossible undertaking in any complete sense. I believe that the best we can hope for is a method that would allow investigators to identify the causal loops that are primarily responsible for enabling complex behavior, for a particular system only, during a particular time period. From this, investigators could identify ways in which the system could be manipulated to be complicated or complex. But, it is important to bear in mind that such tests would only work for idealized and well-described systems. The benefits that such a test would bring to our understanding of real life systems are not at all clear cut. The difficulties confronting the design of such a testing apparatus will become clear as the paper progresses.

From this brief discussion of the possible definitions of a complex system, it is clear that they are insufficient (after all, the notion of incompressibility explicitly denies the completeness of any definition—Richardson et al. [42]). In an attempt to address these shortfalls we might rewrite the initial definition of a complex system as:

A complex system is comprised of a large number of non-linearly interacting non-decomposable elements. The interactivity must be such that the system cannot be reducible to two or more distinct systems, and must contain a sufficiently complex interactive mixture of causal loops to allow the system to display the behaviors characteristic of such systems (where the determination of ‘sufficiently’ is problematic).⁵

A rather circular definition possibly? So a complex system is a (topologically complex) system that displays complex behavior! Despite its circularity, which highlights the problematic nature of defining complex systems, this will be the definition assumed from here on, albeit in a loose way.

The relationship between systems and complex systems is not easily unraveled. If we take the above definitions we could argue that a complex system is a special kind of system as by definition the relationships between its parts are non-linear, whereas the nature of the relationships in the definition of a system are unspecified. However, it could also be argued that a system is a special kind of complex

system because one cannot get non-linear behavior from a linear system, but linearity from non-linearity is possible as a special case definitional scope. It would seem that a general complex system is very broad, as all types of systems are potentially accounted for beneath its. However, it could also be argued that non-linear and linear are not the only types of relationship (though possibly in a mathematical sense they are) and the general system definition is more general. I think that it is difficult, if not futile, to attempt to decide which is the more generic definition. The reason I would like to be able to distinguish between the two, though, is to get a feel for the differences between the general systems community and the complex systems community. Increasingly I feel that these are irrelevant concerns, and that the two communities have almost identical aims though they use rather different tools to fulfil those aims.

One way in which I personally distinguish between the two is that general systems theorists traditionally search for homologies in nature, whereas the complex systems community (in my opinion) fully acknowledges the problematic nature of such a goal (because of the potential of chaos to make two similar contexts evolve utterly differently). Another way to express the difference between the two communities would be to say that general systems theorists celebrate similarity, whereas complex systems theorists, or complexologists, celebrate difference; a distinction, incidentally, which is often used to differentiate in broad terms between modernists and postmodernists. The position developed herein begins with the assumption that the Universe is the only complex system (as defined above), the coherent whole, and so everything else is a manifestation of nature’s inherent underlying complexity: everything, without exception, is complex.

Complex system’s behavior

Complex systems as defined above display some very interesting well-popularised behaviours. The two most dominating forces within a complex system are the forces that push the systems towards chaotic behaviour and those that encourage self-organisation; a fight between disorder and order, if you like, much akin to Anaximander’s notion of elements in conflict (“They ‘pay penalty and retribution to each other for their injustice according to the assessment of Time’”, Gottlieb [19: 9]). I tend to argue that despite this apparent tension chaos is actually a result of self-organisation, i.e., a complex system can self-organise into a structure that leads to a chaotic mode of behaviour (hinting perhaps at the possibility of higher-order parameters); it does not follow that self-organisation necessarily leads to order.

In previous articles (see Richardson et al. [41] or Cilliers [10], for example), it has been suggested that complex systems display the following characteristics:

1. Their current behavior depends upon their history;
2. They display a wide-range of qualitatively different behaviors;
3. As already mentioned, the system’s evolution can be incredibly sensitive to small changes as well as being incredibly resilient to large change (and all possibilities in between);
4. Complex systems are incompressible, i.e., it is impossible to have an account of a complex system which will predict all possible system behaviours⁶.

I had like to revisit these observations herein as my position has subtly changed since Richardson et al. [41].

System history⁷

In Richardson et al. [41], it was argued that a key distinction between complex and complicated systems was that history was of more importance when considering complex systems than it is for complicated systems. The example given as a complicated system was a silicon-based computer, and a social system was given as an example of a complex system. I feel that some comment concerning the role of history as an analytical tool is necessary. The main difference between these two examples is that, for a computer, it is more or less a straightforward issue to determine what its current state is. History as an analytical tool is less important in this case because an analyst could easily account for history’s effect on the computer by directly examining its current state, or configuration (e.g., what software it is currently running).

However, if we take a social system it is nigh on impossible to get such an accurate appreciation of its current state. If we could view its current state directly its future evolution would be quite easy to ascertain (although difficulties associated with non-linearity would still place significant limits on our predictive powers). However, we cannot ever know the current state of each comprising individual (which would require a complete representation of their current epistemic state that would allow us to predict how each person would respond to particular stimuli) and the detailed form of the interrelationships. So, to obtain a clearer picture, or even a very basic picture, of the current state we can examine the system’s history to indirectly develop an idea of what the current state of the system is, thus allowing an informed, though very approximate, prediction to be made about its future. History as an analytical tool is important simply because complex systems are often too opaque to the eyes of the observer; whereas direct observation yields a very accurate picture of a complicated system, such approaches yield little when considering complex systems and so indirect historical methods can be very useful indeed. However, the interpretation of historical data or texts is always open to question, so an appreciation of the current state of a social system based upon its past behavior is always incomplete and bias. It follows that any predictions made from a historical ‘model’ will also be incomplete and biased.

seem inappropriate to talk about it. However, history can be introduced in at least three ways. Firstly, we could mention it explicitly in our definition by suggesting that each non-decomposable entity retains some memory of it’s past. Secondly, we can recognize that the currently observed state (i.e., component states and overall structure) of any complex system is a direct result of its past and so in some sense the past is reflected in the current—this introduces the notion of a system level memory that is not explicitly coded into the system’s components. Lastly, we can recognize that we can never actually have a direct and complete representation of any complex system and that it is our abstractions of a particular system that introduce the idea of local memory. In this case, and as strange as it may seem, memory is not a real feature of any complex system at the level of description offered by the definition above, but a useful concept to help us create useful partial representations. As we shall see later in the paper, quasi-entities can emerge that can exhibit quite different properties from those exhibited by the system’s fundamental components. These quasi-entities can behave in such a way as to appear as if they indeed have explicit memory. So, in short, even if memory is not included in our baseline definition of a complex system, a variety of memories can emerge from within the system in the form of sophisticated quasi-entities.

The role of indirect historical evidence in the development of a limited understanding of the current state of a complex system does not wholly replace the role of direct observational evidence. The argument is simply that history, as an analytical tool, offers another route to the understanding of complex systems over and above that offered by direct methods, whereas for complicated systems a historical analysis would offer little (unless of course you are interested in the overall evolution of computer design (which would be a complex system) rather than the functioning of one particular computer)⁸.

Qualitatively different behaviors and scale independence

As already suggested herein and elsewhere (see Allen [2], for example), complex systems display a variety of qualitatively different behavioral regimes. However, it should be noted that this phenomena is scale-dependent, i.e., the possible qualitatively different behaviors that one might observe depend upon the scale, or level, one is observing. For example, and it is an extreme example, if one could view a social system down at the level of individual quarks (almost at the ‘bitmap’ level of reality) it would be hard, if not impossible, to recognize the qualitatively different behaviors that manifest at the human scale. So the emergence of (quasi-) hierarchical levels helps considerably when trying to understand complex systems (a topic that will recur throughout this paper).

If one attempted to draw a (snapshot of a) phase space portrait of a complex system, it would only be a representation of the possibilities that might occur at one particular level of aggregation/abstraction. Not only will different phase portraits exist at different levels of aggregation/abstraction, but as the different levels interact with each other (which again is scale-dependent) the phase variables (also called order parameters) that are relevant for the construction of a particular phase portrait at a particular level will change, i.e., different phase variables might best reflect the current state and future possibilities of the system than ones that might have previously characterised the system. Not only does the quantitative nature of the state variables change, but the qualitative nature changes also.

The existence of (quasi-) levels, which we shall return to, certainly facilitates the development of understanding for a complex system. It has been argued that each level displays a substantial realism [16] meaning that there exist solid representations of aspects of complex systems that need not include the whole system; an argument for some kind of soft reductionism maybe? (But, I do not want to give the whole story away too early!). I think that this is a very important point as much of the complexity writings I have come across generally trivialize the process by which it is decided whether or not a particular system is complex, or can be legitimately treated as such. It is also rarely acknowledged that even a complex systems description is still a bounded description—an idealization— and therefore still very much reductionist in nature.

Chaos versus anti-chaos

The perturbations that might cause a reaction within a complex system of interest come from outside that system. This is an important point. When analysts build models of organisations, for example, the key implicit assumption that is made is that the decision- maker is outside of the organisation of interest, i.e., a subject–object dualism is implicitly maintained. Analysts, consultants, decision-makers, etc. look at the system of interest, attempt to understand its current state, and use the resulting model to make predictions that support a particular course of action. In this approach, the analyst decision-maker (etc.) is assumed to be outside the system looking-in, trying to push it in a particular direction. Change can come from two general quarters, from within and from without. Change from within is emergent and often inevitable if perturbations from the outside do not act to affect (via changing component relationships) the emergent process. Change from without comes as a reaction to these external perturbations. The two are not independent of each other.

Whether change comes from within or from without, the overall change to the system is problematic to determine. The overall systems behavior might be radically affected, or the system might absorb any attempt to change and continue relatively unaffected. Though, it is important to remember that attempts to change the system (failed or not) may result in delayed changes despite no apparent immediate reaction. Who knows what chain of events might have been triggered; the seeds for a new possibility might have unintentionally been sown.

This distinction of being ‘inside’ or ‘outside’ the system will be revisited again. It certainly raises some interesting issues regarding how useful one can be being outside, and the relationship between ‘outsider’ and ‘insider’ knowledge.

Furthermore, given that the fundamental assumption of this paper is that there is only one coherent complex system (the Universe), how can we even justify the seemingly innocent assumption that other systems exist that can be treated as such? The belief that systems do in fact exist (such as an organization) in interaction with an environment that can be analyzed as such appears on the surface to be such a plainly obvious assumption to make; so obvious in fact that it is rarely considered to be anything more than common sense.

Incompressibility

Bottom-up limitations

In Richardson et al. [42], it was argued that incompressibility is the ‘showstopper’ for a theory of everything, or a comprehensive theory of complexity, and is the key reason in support of a quasi-‘critical pluralist’ philosophy. However, in presenting this work at recent seminars it was argued that if we consider a cellular-automata-type experiment, for example, then it is a trivial matter to have a complete description of such a complex system. How can the importance of the incompressibility of complex systems be maintained if in fact completely describable complex systems do exist? In taking the example of the cellular automata experiment in which everything about the composition of the complex system is readily known, we can say that complex systems are incompressible in behavioral terms but not necessarily in compositional terms. So what makes such an idealized complex system otherwise incompressible? The showstopper is (computational) intractability, i.e., the inability to predict all future states of the system, despite complete compositional knowledge, without running the system itself. There is no algorithmic shortcut to a complete description of the future. Wolfram [52: 735] suggests that “[c]omputational reducibility may well be the exception rather than the rule,” and that for irreducible (incompressible) systems “their own evolution is effectively the most efficient procedure for determining their future” [52: 737]. This is very similar to Chaitin’s definition for a random number series: “A series of numbers is random if the smallest algorithm capable of specifying it to a computer has about the same number of bits of information as the series itself” [7: 48]. This seems to imply that incompressibility is very closely related to the term Chaitin’s notion of randomness. Does this mean that if a complex system is incompressible then it is random? In a sense the answer is yes. But, whether a complex system is random or not depends strongly on one’s tolerance for noise. If one demands complete understanding, then the system of interest needs to be expressed in its entirety and knowledge could only be obtained by running the system itself. However, if one was less stringent in one’s toleration of ‘noise’⁹ then maybe patterns could be found that in a rough and incomplete way would allow for a description to be extracted that would indeed be less than the total description and yet still contain useful understanding. Again, we will return to this issue later.

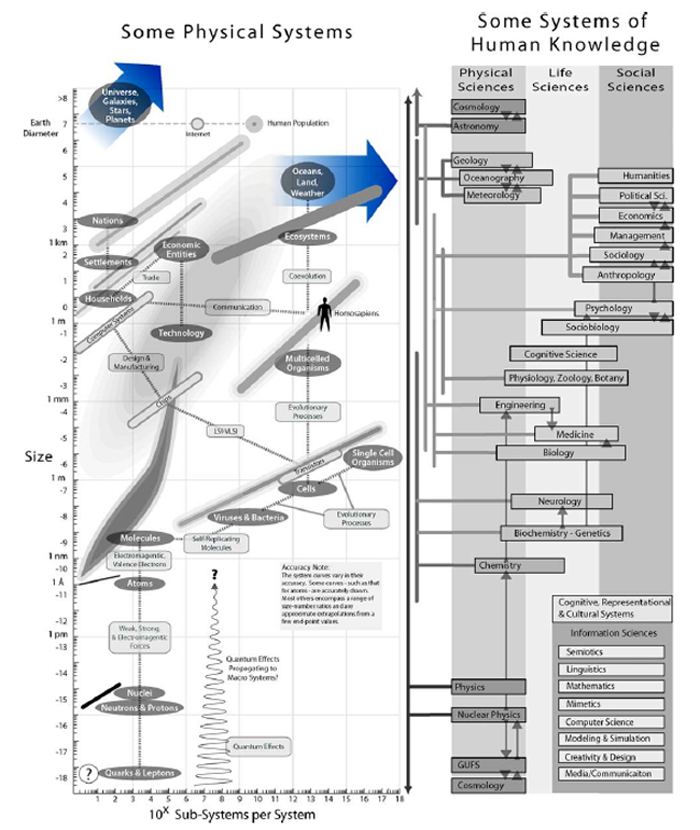
Fig. 1. The reality of hierarchies versus the hierarchy of the natural sciences. (© 2005 Marshall Clemens, www.idiagram.com—used by kind permission.)

An example of the type of incompressibility¹⁰, or intractability, described above is the hierarchy of the sciences (Fig. 1). Chemists, for example, provide a description of reality at the molecular and molecular-complex level. Physics traditionally sits below chemistry as being the more fundamental science considering the constituents of molecules, namely, atoms, quarks and maybe superstrings; chemistry supposedly emerges from physics. However, there is a lot more physics in chemistry than physicists actually know about. The ability to bootstrap from physics to chemistry is well beyond current science. The problem is compounded further if we try to bootstrap from chemistry to biology, which deals with cells and multi-cellular entities. As Douglas Hofstadter [21] remarks in Gödel, Escher, Bach “a bootstrap from simple molecules to entire cells is almost beyond one’s power to imagine” [21: 548]. As we move up the hierarchy, more and more of the noise of absolute reality is omitted. In the absence of a complete bootstrapping method, it is simply assumed that the ontology that each science is based upon is legitimate in itself and that the lower levels can be approximately ignored without too much loss of noise. Bottom-up computer simulations approach their subject matter in more or less the same way. An ontological position is assumed, i.e., the nature and form of the basic building blocks are determined, and the macroscopic behaviour that emerges is deemed more life-like because it emerges from a lower-level ontological commitment; on the surface the models look more like reality, so the conclusions must therefore be more robust. But, how secure are their ontological foundations? As with those of the traditional sciences, the strength and basis of these ontological commitments will be explored later. An extended discussion of the nature of hierarchies from a complex systems perspective is offered in Ref. [40].

Top-down limitations

Even if we can have complete compositional knowledge of a complex system (observable at the human level of existence), intractability places some insurmountable limitations on our possible behavioral knowledge. What limitations are placed on us if we do not even have good compositional knowledge? We might begin by viewing the system at a higher level. At higher levels we can recognize alternative sets of interacting entities that ‘exist’ (or are recognizable as such) only at higher levels. For example, we would be insane to investigate organizations at the level of quarks, but we can make good progress by considering employees to be the fundamental building block. It must be remembered, however, that these higher-level entities are emergent aggregates of those ‘existing’ at a lower level. As such, our higher-level abstractions inherently cannot help but miss something out. These abstractions approximate the complex system by assuming the absolute existence of higher levels and therefore higher entities despite the fact that these higher ‘beings’ emerge from the lower levels; the higher-level existence is assumed to be the emergent properties of the level beneath, which is in turn an emergent property of the level beneath that and so on until the fundamental components (superstrings?) are reached.

Let us assume for a moment that we could speculate as to the nature of the entities and interactions at the level beneath the level we might be interested in (e.g., we might be interested in how an organization functions, so we build an agent-based model that assumes the employees represent the level beneath the organizational level). If we could achieve this then we could construct a model (a computer-based agent model, for example) of the lower (employee) level, which would have as its emergent properties the next higher (organizational) level. We could then speculate as to the composition of the layer below (multi-cellular?) the lower (employee) level, which would again have as its emergent properties the (employee) layer above. In principle we could continue this process all the way down to the bottom level comprised of the absolutely fundamental components (superstrings?) and relationships. However, how could we be sure that at each stage we had selected the correct abstraction? The only supporting evidence we would have would be limited empirical evidence. But, because of the nature of non-linearity there is a huge number of ways to abstract a problem in such a way that will easily be confirmed by our limited empirical evidence, i.e., there is one way to ‘curve-fit’ a linear problem (assuming a fixed number of dimensions) but there is an infinite number of ways to curve-fit a non-linear problem (see Fig. 2). So, the idea that agent-based modelers have better models (and therefore more knowledge) than other modelers is severely flawed, as in principle there is an infinite number of microscopic sets (i.e., members of the lower level) that would lead to, for a certain range of contexts, the desired macroscopic properties (i.e., the level above). As such we still cannot be sure that our knowledge is transferable to any other contexts except those already observed. There is no doubt that agent-based modelling (which for most intents and purposes are simply advanced versions of simple cellular automata experiments) is an advanced method of analysis, and the analysts’ toolset is significantly enhanced with their inclusion, but we should not get too carried away with the suggestion that they are better models of reality. Their similarities with ‘perceived’ reality might run very shallow indeed.¹¹

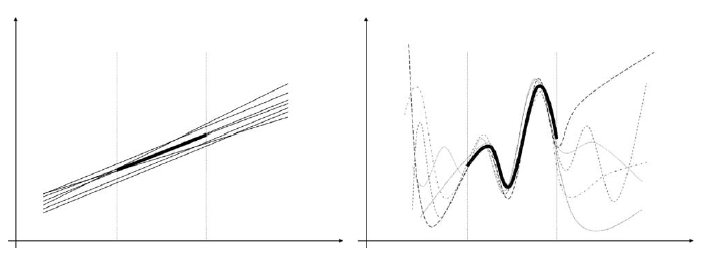
Fig. 2. Linear versus non-linear. In both illustrations the thick line/curve within the two vertical lines represents some set of empirical data for an observed range of contexts. The other lines/curves represent predictive data based on different possible theoretical explanations for those empirical data, and extend beyond contexts for which such empirical data exists. The figures illustrate the difficulties in extending current explanations, or theories, of known contexts to new, as yet unobserved, contexts.

So back to our basic question: “how do we know we’ve chosen the right abstraction?” The short answer is that “we can’t.” But this is not a showstopper by any means for analysis, science, or any intellectual endeavor.

In short, the limits to understanding complex systems come not only from our inability to bootstrap from one level to another in either direction, but also from the fact that the only complete description (if that is what we demand) must be constructed from absolutely the bottom-up (i.e., from universal superstrings upwards) rather than from the top, or middle, down. This does not deny the possibility of developing useful and relatively robust knowledge from starting points other than the consideration of everything. In a simple cellular automata experiment, for which perfect compositional knowledge is known, the future development can only be determined fully if the model itself is run. If we start with limited knowledge of some future development we can never be sure that a model obtained by working backwards will be accurate; we must have complete knowledge to build a *complete *model—a theoretical as well as a practical absurdity.

We will revisit this topic when we come to consider the Universe as such a cellular automata experiment and the limits of scientific knowledge, as well as all other forms of knowledge.

In the argument presented thus far, there has been an undercurrent emerging concerning the nature of boundaries, i.e., the ontological status of boundaries, structures or patterns. Further exploration of the nature of boundaries, and therefore the ontological status of ‘objects’ or ‘entities’, will be the foundation from which an evolutionary philosophy will be constructed and legitimized.

The ontological status of boundaries

This section will discuss the nature of boundaries in a complex system, or the ontological status of objects/entities. Initially, the nature of boundaries from a spatio-temporal perspective will be discussed, followed by an exploration of the boundary concept from a phase space perspective. These two perspectives will then be used to argue for a position in which no boundaries really exist in a complex system (except those defining its comprising components), but that a distribution of boundary (structure) stabilities exist which legitimates a wide range of paradigmatically different analytical approaches (without the rejection of natural science methods). However, in this part of the analysis assumptions are made about the efficacy of variables and their non-linear interrelationships that are not necessarily justified. In what seems to be a back-to-front way, the second part of this section will briefly consider how it is that we can even make such claims about the relationship between modelled boundaries and natural boundaries. The discussion here will be brief, as it will be expanded upon in the section that considers the Universe as a vast cellular automata experiment. I also hope that the choice of presenting these ideas in a seemingly back-to-front manner will also become clear.

Emerging domains

If one were to view the spatio-temporal evolution of an idealized complex system, one would observe that different structures, or patterns, wax and wane. In complex systems different domains can emerge that might even display qualitatively different behaviors from their neighboring domains. A domain is simply defined herein as an apparently autonomous (possibly critically-organized) structure that differentiates itself from the whole (i.e., it stands out from the noise). The apparent autonomy is illusory though. All domains (patterns) are emergent structures that persist for undecideably different durations. A particular domain, or structure or subsystem, may seem to appear spontaneously, persist for a long period and then fade away. Particular organizations or industries can be seen as emergent domains that are apparently self-sustaining and separate from other organizations or industries.

Fig. 3 illustrates the spontaneous emergence of order in a simple complex system (the mathematical details of which are not relevant for this discussion). Different domains emerge whose ‘edges’, or boundaries, change and evolve as the system evolves. Though a snap-shot of the systems’ evolution would show clear structures, it would be wrong to assume that such structures were a permanent and real feature of the system; the structures are emergent and temporary.

Fig. 3. The emergence of domains (or sub-systems).

Though it is argued here that all boundaries are emergent and temporary, some boundaries may persist for very long periods. For example, the boundaries that delimit a proton (which is arguably an emergent manifestation of the combined interactive behavior of quarks, or superstrings) from it’s complement, persist for periods theorized to be longer than the current age of the Universe (possibly > 10³³ s), after which the boundaries decay (through the emission of an X particle) and a new set of boundaries emerge (a positron and a pion, which then decay into three electromagnetic showers). Not all boundaries are so persistent and predictable in their evolution. The boundaries that describe an eddy current in a turbulent fluid (which could be seen as the emergent property of the liquid’s constituent molecules) are short-lived. Most boundaries of interest in our daily lives exist somewhere in between these two extremes. The boundaries that define the organizations we work within, those (conceptual) boundaries that define the context(s) for meaning, the boundaries that define ourselves (both physically and mentally) are generally quite stable with low occurrences of qualitative change, although quantitative change is ubiquitous.

It is also important to remember that the observation of domains, and their defining boundaries, depends upon the scale, or level, one is interested in (which is often related to what one wants to do, i.e., ones purpose).

An example of persistent boundaries and resulting levels again comes from the natural sciences, which has obvious direct connections with the hierarchy of sciences discussed earlier. The hierarchy of quarks→bosons and fermions→atoms→molecules→cells→etc. is very resilient (especially at the more fundamental scales). Choosing which level to base our explanations within is no easy task, particularly as any selection will be deficient in some way or another (refer back to the discussion on top-down or bottom-up representation).

At the level of quarks (even if we could directly observe that level), say, it would be difficult to distinguish between two people, though at the molecular level this becomes much easier, and at the human level the task is beyond trivial (though we are increasingly at risk of believing what we see is what there is simply out of habit). The level taken to make sense of a system depends upon the accuracy required or the practically achievable. Organizations (economic domains or subsystems) are very difficult, if not impossible, to understand in terms of individuals so they are often described as coherent systems in themselves with the whole only being assumed to exist¹².

Fig. 4. The emergence of qualitatively stable behaviours.

In short, the recognition of boundaries is problematic and is related to the level of aggregation (scale) we choose to view or are capable of viewing.

Evolutionary phase spaces

The emergent domain aspect of complex systems is complexified further when the behaviors of different domains are included. Let us assume for the moment that we are interested in a particularly stable domain; a particular organization for example. We might perform some kind of analysis, a cluster analysis for example, that allows us to extract or infer, in a rough and incomplete way, a number of order parameters (i.e., parameters that when changed, change the domain’s behavior) and their interrelationships that seem to characterize the observed domain’s behavior. We can then draw a picture of the domain’s phase space, which will provide information regarding the qualitatively different modes of behavior of that domain for varying time. Fig. 4 shows the evolution of such a phase space for a very simple idealized non- linear system. The two main variables are position (y-axis) and velocity (x-axis) and the two dominant shades represent the two main attractors for this system (black represents an unstable equilibrium attractor). So on the first snapshot (taken at time=0), depending on what the initial values of the order parameters are, the system is either attracted to the attractor represented by the light grey or the attractor represented by the dark grey.

The proceeding snapshots show how the phase space evolves with the two qualitatively different attractor spaces mixing more and more as time wears on. What we find for this particular system is that, though we know that there are two distinct attractors, after a relatively short period the two attractor spaces are mixed at a very low level of detail indeed. In fact the pattern becomes fractal, meaning that we require infinite detail to know what qualitative state the system will be in. Even with qualitatively stable order parameters qualitatively unstable behavior occurs (see, for example, Kan [26]). These are referred to as ‘riddled states’, or ‘riddled basins of attraction’, Sommerer and Ott [46].

Despite this continuous mixing of states, stable areas of phase space do emerge and persist. Fig. 4 shows an example of this by highlighting the emergence of a stable region that persists to the end of the modelled evolution. This is of interest because it demonstrates that not only is quantitative prediction problematic but that qualitative prediction is also problematic (as opposed to being impossible—which is what a number of naïve chaoticians claim). But remember that the example given is for a stable domain with qualitatively stable order parameters. For a domain, that is an emergent property of a complex system having other emergent neighbors, the order parameters will not necessarily be qualitatively stable. The defining order parameters might be qualitatively unstable. (This demonstrates that the order parameters are simply trends that offer a superficial (though often useful) understanding of any real system of interest.) The evolution of these phase variables will depend upon the interaction between the neighboring domains, which is a manifestation of causal processes at the lower levels (an argument for meta-order parameters perhaps). This introduces non- trivial difficulties for any observer’s attempts to make sense, i.e., derive robust knowledge. The fact that such change is not random, with the existence of stable structures as well as behaviors, means that the possibility of deriving useful understanding is not wholly undermined.

Before moving on to briefly consider simple cellular automata and Conway’s Game of Life, a terminological link must be made between the above discussion on boundaries/domains and objects/entities if it is not already apparent. Domains are objects or entities. In this analysis a proton, a tree, a car, a nation state, are legitimate objects that are identified as being persistent and apparently autonomous phase space (as well as spatio-temporal, which is how they are ordinarily recognized) domains or patterns.

But, and it is an important but, how can we justify not only this leap from persistent structures to everyday objects but also that phase variables or order parameters should have any basis in the real world at all? This directly addresses the issue of whether mathematics, or any structured (not necessarily formal) language, has any rights at all in claiming that it can be used to represent all of reality. To explore this concern we turn to cellular automata—the simplest form of all possible complex systems.

Cellular automata

It is not my aim to provide a course in cellular automata (CA) herein, but a brief introduction may serve useful. In a cellular automata world every ‘pixel’ is described and accounted for. No shortcuts are taken to approximate the CAs overall behavior; everything is described and modelled in exact detail. Fig. 5 depicts the evolution of a selection of simple 1-dimensional CA worlds. The first line in each image depicts the starting point for the CA world; every point in that world is described completely. In these examples each world consists of 200 entities that can each take on a black or white state and are each related to their neighborhood through a very simple (non-linear) rule; the fundamental ‘Law of Physics’ for that world, there are no hidden variables or such like. Each subsequent line shows how each world evolves as the interaction rule is applied. What is represented in each image is an exact history of each world (up to an arbitrary point). We might refer to these images as bitmap (BMP) images of these worlds, as they contain all there is to know about each world; they are complete descriptions. Whereas a JPEG description would employ an algorithm to compress the images (i.e., extract trends) via some mathematical shorthand, a bitmap image contains complete and perfect information for each and every element of the CA world¹³.

Fig. 5. Examples of 1-d Cellular Automata World.

There are two very important points to be noted regarding such CA worlds. The first is that changes in the initial distribution of ‘blacks’ and ‘whites’ has little effect whatsoever on the qualitative evolution of the worlds history. The rule of interaction almost completely determines the structure that emerges. Even if the initial conditions were random, the qualitative evolution would be completely unaffected, i.e., the long-term evolution of these CA worlds is quite independent of their starting conditions.¹⁴

Secondly, and possibly more importantly, the reader may notice that for a particular world, different groupings, or entities, emerge; entities that contain 10 black pixels in a row, for example. Not that it is easily appreciated from the examples given, but it is possible to extract some sketchy properties for these entities allowing a rough appreciation of how they might interact¹⁵. How can this be? How can we assign properties, however rough, to groupings of pixels that are simply the result of the application of a universal rule? In a sense, this means that they have an existence independent of the bitmap description that the world is based upon. Here, we see the beginnings of an ontological shift that is simpler than the bitmap ontology, although not as complete. This really is quite a stupendous leap, and well worth exploring further. It is difficult to visualize the ontological shift (shift in what exists) using 1-d CA worlds, so to help illustrate this point further we next consider John Conway’s Game of Life.

Conway’s game of life

As with CA I am not going to include a full description of the Game of Life. The interested reader is strongly encouraged to refer to William Poundstone’s excellent text,

Fig. 6. Objects in the Life universe.

The Recursive Universe [34] and to explore Paul Callahan’s [6] interactive website¹⁶ (though other examples are easily found). For the purposes herein, I will simply regurgitate Dennett’s [14: 37] brief introduction to the Game of Life, or Life.

“Life is played on a two-dimensional grid [as opposed to the 1-d examples already given], such as a checkerboard or a computer screen; it is not a game one plays to win. The grid divides space into square cells, and each cell is either ON or OFF at each moment. Each cell has eight neighbors: the four adjacent cells north, south, east, and west, and the four diagonals: northeast, southeast, southwest, and northwest. Time in the Life world is also discrete, not continuous; it advances in ticks, and the state of the world changes between each tick according to the following rule. Each cell, in order to determine what to do in the next instant, counts how many of its eight neighbors is ON at the present instant. If the answer is exactly two, the cell stays in its present state (ON or OFF) in the next instant. If the answer is exactly three, the cell is ON in the next instant whatever its current state. Under all other conditions the cell is OFF.”¹⁷

The entire physics of Life world is captured in that single unexceptional law.

What one finds in exploring the Life world is that some structures emerge that seem to be entities unto themselves. Despite Life being a simple recursive system, these entities seem to maintain themselves and move around the checkerboard in quasi-determinable ways, as well as ‘interact’ with other entities (see, for example, Poundstone, [34, Chapter 2]). Fig. 6 illustrates this to a very limited degree. Along the top of the figure from left to right are four such entities that have been named ‘loaf’, ‘boat’, ‘beehive’, and ‘ship’, respectively. There are many others such as ‘blinkers’, ‘period-2 oscillators’, ‘gliders’, etc. The main image in Fig. 6 is a snapshot in the history of a Life configuration known as ‘Puf Train’ [6]. Now we can get to the heart of the Life matter. Again, in Dennett’s [14: 39] words:

“. should we really say that there is real motion in the Life world, or only apparent motion? The flashing pixels on the computer screen are a paradigm case, after all, of what a psychologist would call apparent motion. Are there really gliders that move, or are there just patterns of cell state that move? And if we opt for the latter, should we say at least that these moving patterns are real?”

Whichever way one chooses to go with the answer to this question, one must bear in mind that Life researchers have discovered rules of interaction for these entities which implies that “their salience as real things is considerable, but not guaranteed” [14]. So even though we can be sure that these entities do not really exist, the fact that they can be treated as having some degree of existence is a staggering breakthrough as it allows us to work with a higher- level (JPEG), albeit approximate, ontology other than the BMP one. These entities, or parts, can be used to construct a high-level system that would be nigh on impossible to do if we were restricted to the BMP domain. In short, Life shows that we can legitimately invoke alternative higher-level quasi-ontologies that are reasonable approximations of the absolutely correct BMP ontology, in which only ON/OFF cells exist. Complex systems are therefore tractable, or compressible, to a degree.

Again in Dennett’s words, [14: 39] what is so incredible with Life is “that there has been a distinct ontological shift as we move between levels; whereas at the physical [BMP] level there is no motion, and only individuals, cells, are defined by their fixed spatial location, at this design level we have the motion of persisting objects.” This observation will be central when we try to paint a picture of a CA Universe in the next section, and justify the legitimacy of not only science but other types of knowledge. Before we move on, I will summarize the discussion thus far presented concerning the ontological status of boundaries from a complex systems perspective by simply saying that there exists a continuum of quasi-boundary stabilities which both facilitates and hinders the development of knowledge of any kind. One other point to remember is that Life is perfectly deterministic; if the game is rerun with the same rules and configuration, exactly the same history will be produced; “[e]verything that happens in Life is predestined” [34: 25]. To be exact, what we should say is that Life is forward-deterministic but not backward-deterministic as “a [particular] configuration has only one future but (usually) many possible pasts” [34: 48].

Exploring the universe as a complex system

Though the difficulties in fully understanding complex systems are considerable, they are not insurmountable, particularly if one can assume that well-defined isolated complex systems actually do exist and can be easily identified. However, I will argue in this section (following on from the previous argument) that no systems actually exist in a strict sense. This observation may seem to be rather trivial, but the methodological differences that arise if the notion of a complex system is problematized are considerable. In this section I will explore the implications of assuming that there is only one true system and that is the Universe itself—an indivisible whole. Though it is impossible to prove in any scientific sense, I begin by making the assumption that the Universe is a CA experiment, in that it comprises an unimaginably large number of non-linearly interacting elements. Why would we want to consider this to be the case? To realize Laplace’s dream of having absolutely Truthful knowledge then, “[t]he state of everything—everywhere—at every time—must be defined. The most economical way to specify such information is through a complexity-generating recursion of physical law” [34: 231] like in Life. According to the latest physical theories these interacting elements might be incredibly minute superstrings that oscillate in 11-dimensional ‘space’, where the oscillation frequency of a string corresponds to a particular fundamental particle, such as a top-quark for example. This view of the Universe is incredibly simple, yet it has the capacity (because of the recursive application of a simple non-linear rule) to account for everything we observe in our view of reality and a lot more besides. It is the capacity of non-linearity to create an infinitude of different structures (and sub-structures) and behaviors that lead to this possibility. Conway, the inventor of Life, “showed that the Life universe...is not fundamentally less rich than our own” [34: 24].

A cellular automata Universe and the status of scientific knowledge

Imagine if you will have a 11-dimensional (a little hard to imagine I know) CA model comprising a vast number of ‘superstring’ automatons whose evolution is determined by a single simple rule; the fundamental Law of Physics. Each step in the Universe’s evolution is simply the result of this rule being applied to each automaton. This view is impossible to prove of course—like other Theories of Everything (ToEs) endeavors it is more ironic science [22: 3] or pseudo-science, than science—but its explanatory powers are surprisingly impressive indeed¹⁸. Though the CA perspective cannot be conclusively proved, an exploration of the consequences that lead from this picture are very revealing. These consequences bring us no closer to a proof of the model, but they do demonstrate the utility of this approach; its capacity to provide a common context for many different discourses is quite impressive indeed.

A deterministic Universe

The first observation is that such a Universe would be completely 100% deterministic:

“. in the Life world. there is no noise, no uncertainty, no probability less than one. Moreover, it follows. that nothing is hidden from view. There is no backstage; there are no hidden variables.” Dennett [14: 38].

The entire evolution of the Universe would be totally predetermined by the characteristics of the comprising superstrings and the one (non-linear) rule of interaction. This would please our scientific forefathers’ view of a Universe as a perfectly tuned machine. For such a construction it is quite possible that there is not even any need for particular initial conditions; the initial conditions could be completely random and the consequent Universe would still be the same. (The initial conditions of the Universe have been a hot topic of discussion for sometime. It is only recently that it has been suggested that maybe there are models of the Universe that do not require initial conditions in the traditional sense at all (Chown [8]; and Tegmark [48])—as with the 1-d CA experiments earlier, the initial configuration might be random with qualitatively the same consequences.) This suggested model of the Universe is based upon a radically realist ontology; what truly exists are ‘11-d superstrings’ (or, whatever turns out to be the viable candidate, although scientists may never know), no more, no less. All other objects, entities, ‘boundaries’, whatever, are no more than different combinations of ‘cell states’ that manifest themselves as the ‘loaves’, ‘ships’ and ‘beehives’ of Life. In this Universe a fermion is a type of ‘boat’, say, having no absolute existence, but having a substantial realism, so substantial in fact as to often allow its absolute existence to be taken for granted. An atom is no more than a ‘fleet of ships’ in this Life Universe. Even we humans are not as we appear to ourselves. We are not sentient beings with free will and learning capacities. A human is just a collection of interacting ‘boats’, ‘ships’, ‘beehives’, ‘super-beehives’, i.e., a very intricate ‘cell state’ whose occurrence is inevitable in a CA Universe.

A CA Universe would allow other ontologies to be assumed without having to deal directly with the BMP ontology of an unimaginable number of interacting ‘superstrings’. It is of the utmost importance to acknowledge that such ontological shifts are imperfect; the complexity of a CA Universe is indeed tractable, but at a cost. But, it is this very ability to profit from alternative quasi-ontologies that enables science to function at all. Without this characteristic mathematics could not exist at all; mathematics deals with ‘loaves’ and ‘ships’, not with Life ‘cell states’. Indeed, it is this very point that even allows the existence of a being capable of making such ontological leaps in the first place.

Another fascinating outcome of assuming a CA Universe is that there is no adaptation in any absolute sense of the term. At the BMP level, the ultimate objective reality, ‘superstrings’ do not learn new tricks; they do not become ‘superduperstrings’ (unless it is through an ontological shift on our part). Adaptation is a feature of an ontology that scientists have chosen to take for granted; it is a way of usefully understanding the changes in the Life ‘cell states’ without having to deal directly with those real ‘cell states’. So when complexologists are heard speaking of complex adaptive systems (CASs), they are taking some enormous strides away from what absolutely exists. A great number of assumptions have to be made before one can even infer the (quasi-) existence of CASs. So, even the ontology that complexologists hail as the best lens to view certain ‘parts’ of the Universe through, are kidding themselves to some extent. Even the CAS ontology is a poor to reasonable JPEG approximation of the absolute BMP reality.

And what of causality? Causation as a necessary connection between two events in a CA Universe cannot be inferred from correlation or association in any real sense. Causality, like Life’s ‘boats’ and ‘ships’ is an emergent ‘cell state’ pattern that can only be recognized as such by making an ontological shift away from the BMP view that assumes it’s existence. Causality as experienced by us mere mortals, is an abstraction rather than a real operating process. The psychotherapist Carl Jung wrote (with the cooperation of the eminent physicist Wolfgang Pauli) an interesting treatise on this exact point: what “if the connection between cause and effect turns out to be only statistically valid and only relatively true.”? [25: 5]. Though as Hume has already noted, “causation is a notion fundamental to human cognition, so fundamental that it is unlikely to ever be eradicated” (Wagner [51: 83]), and so it shouldn’t. Whether causation is real or not, it has proven to be a very productive concept.

A theistic observer

In the CA view of the Universe there is no room for free will and choice—that would go against the whole notion of determinism. Consciousness does not exist as such. All decisions, actions, utterances that we each make were all predetermined from the moment of creation (assuming that the idea of a beginning, and therefore time, actually makes any sense in this context)¹⁹:. Even the fact that I am sitting in my home office in Norwood, MA at 10:30 in the morning, composing this specific paragraph was inevitable (once the initial conditions had been selected²⁰)²¹. This all sounds a little absurd, though there are devout religionists who would be quite prepared to believe it. But assuming that the Universe is deterministic, who or what would this apparent exquisite determinism be visible to? Cilliers [10: 4–5] has argued that no thing that exists within a complex system can have complete knowledge of that system. For us, as mere mortals participating within the Universe, we would have to construct a model that represented all 10⁹³ [9], or whatever the colossal number is, of superstrings that made up the Universe and step-through the overall evolution. Now, given that we’re inside the Universe and only have limited resources available to us from within that same Universe, how could we possibly represent the entire Universe with only part of the Universe available to us? Again the simple answer is that we cannot²².

From this simple argument it is clear that, if the Universe is indeed deterministic, this determinism is (thankfully) beyond us; we will never conceive of an experiment that would otherwise persuade us of our own sentience. The Universe’s determinism could only possibly be visible to an external entity; a theistic (meaning outside) being. If you like, this is God. However, such a God would have to have sufficient resources available to model the entire created Universe. To It, the determinism of the Universe would be plainly apparent (assuming the Model ran faster than the Universe itself) like the determinism of the CA experiments in previous sections is plainly apparent to a human observer. Furthermore, given that a model of more degrees of freedom, i.e., greater complexity, than the Universe itself would have a richer set of behaviors than the Universe, this model would have to be the same as the Universe; the Universe itself is its best model. And, assuming that intractability also restricts a theistic being, then It would have to run It’s deterministic universal model before the Universe was created to ensure that it turned out as desired (because there would be no algorithmic shortcut to the future—unless It was happy to rely upon a scrappy JPEG version, which would give unreliable results)²³. Of course, some would argue that such an entity would not be limited by such human limitations.

However, we are not totally blind to the Universe’s inherent determinism. The fact that ‘we’ even exist and that ‘we’ have constructed Laws (from the mathematical representation of ‘loaves’ and ‘boats’) that allow us to make quite accurate predictions, accurate enough to build technology, for example, shows that we do indeed obtain glimpses of the clockwork Universe.

Theism versus atheism

From within the Universe it is impossible to have an absolute representation of anything. There is only one true system; all other systems are temporary and contingent structures whose boundaries are, in a strict sense, illusory. In the sense that boundaries are hard resilient objects that demarcate the part from the whole, no boundaries actually exist (except those that define the Universal Cellular Automata). Despite this no-boundary hypothesis, which naturally demands an unachievable radically holist approach to knowledge creation if one wants True knowledge, models that do indeed assume boundaries do have considerable practical use.

Though it is interesting that such a complex systems view does lead to differences in knowing dependent upon a theistic (without) and atheistic (within) position, it is not of much help to us as members (however unreal) of the Universe. However, it is interesting that such a vision of the Universe provides a common context that allows the Universe to be both deterministic and non-deterministic, depending upon the position of an observer. Such a vision has the capacity to allow for the co-existence of apparently opposing positions. However, though it may seem to provide little value when considering the Universe as a whole, what if we could approximate parts of the Universe that appear to be real systems in their own right as complex systems, or even CASs? Again, it is the ability to associate substantial realism to the various Life entities that facilitate (or even allow) this activity. Our own existence as such can only be realized by making a shift from The Universal Ontology of Life to an irrealist (albeit substantially real) ontology; human existence is an arbitrary paradigm rather than a given absolute fact.

The complex systems view differentiates between the knowledge one can obtain when we regard ourselves as outside a (particular) system (of ‘loaves’) and that knowledge we can obtain when we regard ourselves as a member of the system. This view demonstrates that the subject–object distinction often made does limit the knowledge we can have. How much can an outside consultant know about a particular organization and how valuable is his/her knowledge? What is more important, the opinions of members of society, or the view of politicians often seen as disengaged from society? How much can an earthbound science know about the Universe in which it is supported? We will not investigate this aspect of complexity much further but, it is interesting to note that complexity thinking does legitimize subjective knowledge as well as objective knowledge, albeit in an imperfect way. We need to ask ourselves: if science claims to extract real patterns (which from the discussion on Life has shown not to be the case—science considers ‘loaves’ and ‘blinkers’ that do not ultimately exist) to what extent are those patterns more real than the patterns we each extract from our surroundings in the process of sense-making. Are our personal opinions based upon patterns less real than those found in science? Why should science be allowed to claim that the objects it considers are more real than the objects we each ‘see’ in our daily lives? In what sense are the boundaries of an ‘electron’ more real than my own personal boundary that defines ‘friend’ given that neither is absolutely real? (Often, the ability to make accurate predictions is the only differentiating factor, which is quite unreasonable given the different nature of these entities.)

Boundary (or, pattern) distributions

The basic conclusion that the complexity-based argument given thus far leads to is that there are no boundaries in the Universe except those that define its fundamental components (superstrings?). How are we to do derive knowledge of particular systems then (particularly if no systems really exist)? As mentioned above the situation is not as dire as it might immediately seem. There is no need to follow the radical holists to model the world, the Universe and everything (which we could not do even if we wanted to). In the field of complexity there is strong evidence that, though there may be no boundaries, there are resilient and relatively stable emergent structures, or patterns, that can be treated with a reasonable degree of accuracy as having limited existence. In fact, there is a distribution of boundary, or entity, stabilities. No evidence is given herein for what this distribution may actually be; it is simply argued that there is a distribution. Fig. 7 illustrates a possible stability distribution (which has no theoretical or empirical basis).

Fig. 7. A possible distribution of natural quasi-boundary (pattern) stabilities.

At one end of the stability spectrum there are boundaries/structures that are so persistent and stable that, for most intents and purposes, it can safely be assumed that they are in fact real and absolute. Boundaries that describe the objects of science-based technology exist toward this end of the spectrum. Such long-term stability allows a ‘community of enquirers’, e.g., the scientific community, to inter-subjectively converge on some agreed principles that might actually be tested through experiment. Under such conditions it is quite possible to develop quasi-objective knowledge, which for most intents and purposes (but not ultimately) is absolute. The existence of such persistent boundaries, or patterns, allows for something other than a radically holistic analysis—this explains why the scientific program has been in many ways so successful when it comes to technological matters—it has hit upon a very powerful quasi-ontology. In many circumstances reductionism (the assumption that ‘beehives’ actually do exist, and act as the ‘parts’ for more complex ‘wholes’) is a perfectly valid, though still approximate, route to understanding. In short, what is suggested here is that scientific study depends upon the assumption that natural boundaries are static in a sense, and that if one can ‘prove’ that the boundaries of interest are in fact stable and persistent, then scientific method is more than adequate.

It is exactly this stability, this apparent ‘movement’ of persistently stable entities (as is observed in Life), that can be attributed some substantial level of realism that allows us as modelers/scientists/observers to “proceed to predict—sketchily and riskily—the behavior of larger configurations or systems of configurations, without bothering to compute the physical [BMP] level” [14: 40]; an enormous computational saving indeed. It is exactly this substantial realism of levels, or quasi-entities, that supports the efficacy of the hierarchy of sciences without having to know everything there is to know about each ascending level away from the fundamental physical superstring reality (in an absolute sense).

At the other end of the stability spectrum we have essentially noise, in which the lifetime of apparent boundaries might be so fleeting as to render them unrecognizable as such and therefore unanalyzable. Under such circumstances attempts to develop knowledge are strongly determined by the whims of the individual, with observed boundaries being more a function of our thirst to make sense, rather than an actual feature of reality. To maintain a purely positivistic position, one would have to accept radical holism and consider the entire Universe—a practical absurdity and a theoretical impossibility, as has already been stated. This is the only method by which truly robust knowledge could possibly be derived.

Fortunately though a vast majority of the perceived Universe is not quite so nebulous. This does not mean, however, that boundary recognition and allocation is a trivial exercise. In fact without the ability to not only determine the stability distribution, but also recognize where the objects of interest might exist on the continuum of stabilities, it is very difficult to determine how to approach them. Radical positivists might argue that a rigorous implementation of scientific method is appropriate across the board. I have already suggested that the application of scientific method makes clear assumptions about the ontological status of boundaries that I believe cannot always be supported, which sympathizes with Shweder’s [44] argument that, as science was designed to study observable material entities that can easily be located in time and space, there are subjects beyond the proper realm of science. Relating this back to Life: the ontological leap from the physical (BMP) reality to the ‘design [JPEG] level’ [14] of ‘loaves’, ‘boats’, ‘ships’, etc. is imperfect, therefore some, what is generally referred to as noise, is removed to allow the leap to occur. Science does not, and cannot, deal with the noise. I would argue that the social sciences, with their willingness to work with a plurality of (possibly incommensurable) methods and perspectives, to view the patterns from different angles and therefore at different noise levels, is more suited to deal with a state of affairs in which both boundary recognition and allocation are deeply problematic. This position reflects Cilliers’s [11: 142] concern that “[i]n accepting the complexity of the boundaries of complex systems, we are committed to be critical about how we use the notion since it affects our understanding of such systems, and influences the way in which we deal with them.”

A short detour—Buddhist philosophy

The view that there is only one whole and that no boundaries exist resonates strongly with Buddhist philosophy, which argues that there are no separate objects in an absolute sense, and that ultimately even consciousness is an illusion. In Buddhism it is said that all things (the whole) are contained in each individual thing—a holographic view of the Universe perhaps? The following quotation from Simple Buddhism [45: 23] illustrates the deep linkage between Western complexity thinking as espoused herein and Eastern philosophy, especially Buddhism:

“. concepts [are] inadequate to convey the essence of enlightenment, yet concepts [are] still essential—that is, concepts [are] both inadequate and essential. Recognizing that all phenomena are interconnected, no philosophical position can be taken without being refutable. [N]o philosophical position can be supported without question, without bias. No ultimate certainty exists. This leaves us with one option: emptiness, which we cannot even call emptiness without error! Emptiness is the unifying basis for all philosophies, an ultimate ground that all philosophies share.”

The discussion, thus far, in some way provides a quasi-scientific argument in support of the above quotation. A practical consequence of Buddhist thought is that we must beware of the temptation to reify our conceptual boundaries [33]. The dereification of conceptual boundaries and the recognition that they are reflections of Life’s ‘loaves’ and ‘oscillators’ is a central part of complexity thinking.

ToEs

Laughlin and Pines [29: 28] define a ToE as: “the ultimate theory of the Universe—a set of equations capable of describing all phenomena that have been observed, or that will ever be observed.” It is clear from the CA description of the Universe from within that I do certainly support the view that there might indeed exist some ultimate realist theory of everything (although the details are elusive, the qualitative nature of it are provided herein, i.e., the ToE will be a representation of an ensemble of automata of dimension n—which is currently speculated to be about 10 or 11—governed by one simple non-linear interactive rule). However, given the difficulties in making accurate abstractions (Buddhists would argue that all abstraction is illusion) from limited evidence, as discussed earlier it is impossible for us to ever know if our proposed ToE is the unique ToE as there are many ways to draw the same conclusions²⁴. Furthermore, even if we could obtain sufficient evidence to demonstrate that we have the ultimate ToE, its value would be questionable. Bootstrapping from one level to another is hard enough in simpler cellular-automata-like models (though Life shows that it can be done in a crude manner), let alone CA models that contain an astronomical number of non-linearly interacting superstrings. So, a ToE does exist, but its use will be incredibly limited, unless of course we somehow overcome the fundamental limitations of computational intractability (as well as not having access to the entire Universe’s resources simultaneously!). To dream that scientists might bootstrap from superstrings to cells or social systems is nothing more than that—a dream.

So what options are we left with? A biological description of humans, for example, is incomplete because it makes assumptions about the efficacy of particular cellular, or multi-cellular, boundaries that are not completely true. At least with Biology, the subject matter presents itself in a manner that justifies the isolated study of well-defined objects. What if we considered a social system? What boundaries would we infer? How might we define the system? What language (which itself depends upon boundary allocations) would we use? The first step in dealing with this ‘grey’ state of affairs is to acknowledge the metaphorical nature of all representation systems, including mathematics.

Theory as metaphor

Given that there are no True boundaries, we are forced to assume boundaries because of our limited resources. Some of these boundary judgements will be reasonable (the possibility to leap fruitfully from the physical level of Life ‘cell states’ to the design level of ‘ships’ demonstrates this), some of them will not be (because of noise). Given that there can be no complete description, it is easy to conclude that all descriptions must necessarily be metaphorical in nature. Even mathematical models are metaphors for reality. A metaphor is a partial description of one thing in terms of another. In the case of mathematics, the Universe (one thing) is partially described in terms of selected mathematical constructs (i.e., other things). As all explanations must be, by their very nature, metaphorical then we must treat them as such rather than implicitly assuming that our explanations are isomorphic with the objects they claim to describe. This is not as big a disaster for our scientific knowledge as it might first sound. Though we might never obtain the Truth, all our words, concepts and theories can point toward the Truth without ever fully expressing it. Our supposed Truths still make ‘useful fictions,’ or as Stewart and Cohen [47: 37] refer to them, ‘lies-to-children.’ As the eminent French physicist Louis de Broglie once said: “May it not be universally true that the concepts produced by the human mind, when formulated in a slightly vague form, are roughly valid for reality, but that, when extreme precision is aimed at, they become ideal forms whose real content tends to vanish away?”²⁵.

To suggest that science, particularly physics, is metaphorical in nature would be verging on blasphemous to some scientists who wish to distinguish their efforts from the ‘soft’ ways of social science, or the humanities. Maybe this is because “[m]etaphors are often construed to be ‘as-if’ devices and hence to have no place in a proper scientific description of the world which pretends to tell things as they are”²⁶ (Bradie [5: 160]). I personally know a number of natural scientists that would be deeply offended at the accusation that science is no more than metaphor. But they need not be so defensive. Science is obviously one of the most successful metaphors ever constructed. Not all metaphors are created equal! However offensive the term metaphor might be to some, its importance lies in the explicit recognition of science’s weaknesses as much as its strengths. “Ordinarily, a metaphor suggests an analogy or likeness between two different things by applying the term for one to the other” [24: 3]. This is exactly what happens when the leap from ‘cell states’ to ‘ships’ is made. As Colin Turbayne points out, “the use of metaphor involve both the awareness of duality of sense and the pretense that the two different senses are one” (quoted in Jones [24: 3–4]). I think that the realist position developed herein justifies the view that all theory is metaphor²⁷. The problem is that “when metaphors become crystallized and abstract, cut off from their roots in consciousness, and forgotten by their creators, they become idols” (p. 5)²⁸. So in pushing this point, I am trying to warn against the idolatry of science; “[i]t is here that the risk may occur that. [a particular] model becomes the sole object of the scholar’s preoccupations” [12: 1070].

Science, however successful, is built upon an ontological shift away from the absolute reality of Life’s ‘cell states’, and is therefore inherently imperfect and limited in scope. On the other hand I do not accept Jones’s [24] position “that the predictive power of physics was built in and guaranteed from the beginning” and that “[t]hrough a selective creation of quantities and laws, a self-contained system was constructed which gives answers on its own terms and arbitrarily rules out what it cannot deal with as non-quantitative or non-physical” [24: 44]. To my mind, science is more than a self-fulfilling prophecy; the existence of science, is an inevitable result of a CA Universe that contains objects whose substantial realism allows for science to make such claims of objectivity. The idolatry of science is simply an unfortunate byproduct of its own success, and scientists’ general failure (consciously or not) to communicate their favored topics’ shortcomings to the wider ‘user’ community.

Now that a complexity-based picture of the Universe has been painted and explored, I would now like to turn toward a possible philosophical solution to the problems that such a portrait conveys. Again, the argument to come hinges on the ability to make ontological shifts, however ‘sketchily and riskily,’ away from the truly physical world of Life ‘cell states’, as well as our answer to the question of how substantially real an ‘object’ or ‘pattern’ has to be before we can safely assume its existence.

Towards an evolutionary philosophy

The first step in making an argument for an evolutionary philosophy is to justify ontological (or metaphysical) pluralism. In a way, this step has already been justified (in an incomplete way—theoretically at least) by the observation that a leap from the physical ontology of Life’s ‘cell states’ to a design ontology in which the apparent objects of the physical ontology can be treated as such, i.e., rather than regarding them as useful ‘non-real’ approximations, they are accepted as having substantial realism that often masquerades as full-blown realism. The hierarchy of the sciences exploits this feature of Life’s ‘cell states’, creating a hierarchy of entities from superstrings to galactic clusters. Each science is justified with the assumption that its objects of study are real. Complexologists do not quite support this view. They argue that each subsequent layer of the hierarchy of entities is an emergent property of the layer below. So, rather than seeing cells (as in biology) as real, they are regarded as the emergent products of the molecular (as in chemistry) layer. The problems of bootstrapping from one layer to another have already been discussed (the intractability of the emergent process basically prevents this from ever happening), and though each of the distinct branches of science probably accept that its particular objects of interest are not real in an absolute sense, the assumption that these objects have substantial realism is sufficient to not undermine their efforts much at all. The fact that each science has indeed made great contributions to human understanding is a testament to the accuracy of these various ontological assumptions for certain purposes. In the absence of a bootstrapping method from the physical BMP model, quasi-‘ontological pluralism’ has been rather profitable. It is quite astounding that science has progressed so far based on poor to good ontological assumptions, but this realization could only be achieved if the Universe was indeed quite stable (in many respects), and again is testament to the power of the ontological shift discussed earlier.

In summary, even though there is a strong argument that suggests that there is only one absolutely real level of existence (the BMP level), we are forced on practical grounds (and justified on theoretical grounds) to at least adopt a scientific pluralism that works rather well indeed. Above I refer to this as quasi-‘ontological pluralism’, in recognition that each of the scientific ontologies are only approximate ontologies, and also that there are only a limited number of these approximate ontologies in science meaning that it is not totally pluralistic. Maybe I should simply say that, according to science, there exist a limited number of substantially real levels.

Horizontal and vertical pluralism

Even though the above view has the capacity to allow the exploration of the same phenomena from different ontologies, all the ontologies are scientific in nature. This view is exemplified by W.V. Quine’s brand of ontological relativism. “Here the plurality consists in the possible existence of a range of alternative scientific worldviews, each empirically adequate to more or less the same degree, and none, even in principle, have privileged claim to provide a ‘truer’ description of the world” Price [35: 389]. Even “incompatible theories can explain the same facts equally well and make equally good predictions”, Masini [30: 279]. Price [35: 389] goes on to argue that,

“[t]here may be equally valid possible scientific worldviews, but all of them are scientific worldviews, and in that sense are on the same level of linguistic activity. In other words, this is what might appropriately be called horizontal pluralism.”

But why should pluralism be restricted to the horizontal? Why should pluralism be associated only with what we might call ‘discourse monism’? The answers to these questions again party depend on how substantially real an entity must be for it to be assumed to be real, absolutely complete, (remembering that it has already been argued that no scientific worldview is based on a real ontology). Scientists would undoubtedly argue that the patterns they develop Natural Laws for, as part of their ongoing investigations, are more real than the patterns that society, or even individuals, deem real. Given the (stable-ish) objects of scientific investigation, then I would generally support this assertion. However, like some social scientists I believe that the subject matter of the social sciences, as an example, puts them outside the proper realm of science (see Shweder [45]). The CA view of the Universe also supports this position. (Note that this belief certainly does not deny the possibility that more traditional scientific approaches have a lot to offer the social sciences). Science is quite intolerant to noise. Scientific methods generally seek to extract clear patterns from the noise of reality. Sometimes this process is straightforward, sometimes it is not. My point is simply that the pattern extraction process is generally problematic depending upon the relationship between an observer and the noise of reality. Substantially “real but (potentially) noisy patterns abound in. the Life world, there for the picking up if only we are lucky or clever enough to hit on the right perspective” [14: 41]. Traditional science has a knack of extracting the more apparent patterns and expressing their form in an implementable way (generally through mathematics). What about everything else? Returning to Price [35: 390]:

“If these [scientific discourses] are cases of horizontal pluralism, what would be a vertical pluralism? It would be the view that philosophy should recognize an irreducible plurality of kinds of discourse—the moral as well as the scientific, for example. This is the species of pluralism with which we. [should] be most concerned.”

Price refers to this type of vertical pluralism as discourse pluralism. Here, we have arrived at a description of what is meant by pluralism in an evolutionary philosophy. This type of pluralism is not irrealist at all. It simply accepts that in the absence of a completely realist position, we may profit from the examination of a variety of other worldviews and discourses whose scale of compression varies. Different scientific worldviews may be as useful as different moral worldviews or different artistic worldviews (such as cubism or abstract expressionism), all of which are metaphors, or caricatures, of reality. This does not lead to an ‘anything goes’ postmodernism, except as a starting point. But how, if we are to make a decision one way or another, are we to untangle the pluralist web and agree upon, albeit temporarily and locally, a dominant worldview?

Critical dialogue as conceptual investigation

It would be convenient to address the question above by simply offering a systematic framework that we could employ that would associate each discourse and comprising worldview with a context in which we could be confident that we had selected the best position to base our decisions upon. The problem with any such approach is idolatry or reification, so I will not attempt to provide a coherent framework except to suggest that there are an enormous number of ways to exploit pluralism, each with their own idiosyncrasies (see as examples Jackson and Key [23]; Flood [18]; or Midgley [31]).

Here I simply argue that it is through critical dialogue that we may temporarily reshape the default position of pluralism to a local monism, i.e., it is through critical dialogue that the general is tailored to the perceived specific. Critical dialogue here is regarded in much the same way that Socrates and Plato regarded criticism, i.e., “no more baffling an enterprise than investigating a concept” [19: 174]. The process is one of an ongoing three-way dialogue between a decision-making body (which may be the one or the many), the perceived context (which will undoubtedly evolve), and the pluralist realm of ideas and theories. The relationship between these three elements is certainly non-trivial and would require extensive investigation to understand fully. But the essence of this process is that the default position is ‘nothingness’ and that through a critical process ‘something’ is negotiated that will inform our actions; it is a group decision process (on which there is a wealth of literature already in existence, see for example, Vennix [50] and selected chapters in Mingers and Gill [32] on multi-methodology). The process is imperfect and explicitly acknowledges the potential of all perspectives, and is ultimately determined on changing pragmatic, rather than rigid ideological, grounds. As Dennett [14: 49] writes, “[t]he choice of pattern would indeed be up to the observer, a matter to be decided on idiosyncratic pragmatic grounds.” I have referred to this evolutionary philosophy elsewhere, Richardson [37, 40] as quasi-critical pluralism (Q-CP). The ‘quasi’ is included to explicitly acknowledge the impossibility of being critical-without-bias or pluralistic-without-limits.

This view denies the sort of (naïve) realism that perfectly maps our conceptual boundaries (that are implied by our explanations) to real objects (despite being ‘constructed’ from a purely realist ontology). There is no one-to-one mapping of our ideas, scientific or otherwise, to objective reality. However, this denial of realism (as a default position) does not recoil into an argument for constructivism. Constructivists (of a particularly extreme bread), as I have already said, argue that all boundaries are created in our minds and as such do not correlate directly with objective reality at all. Q-CP is based upon the distribution of natural boundary/pattern stabilities (derived from a purely physical foundation) and falls between these two extremes. Rather than having a fixed relationship with natural (quasi) boundaries, or having no relationship at all, our conceptual boundaries do have a complex and changing relationship with reality. Sometimes this link might be so tenuous as to be unusable. Sometimes this link is so strong as to give us the impression that we might actually have absolute Truth to hand. The key difference between this position and (naïve) realism is that it explicitly acknowledges the problematization of boundary recognition, which is trivialized in many realist philosophies. The key difference between Q-CP and constructivism is that Q-CP acknowledges that the world of substantially real patterns does play an integral part in the evolutionary relationship between reality out there and our ideas. Fig. 8 attempts to illustrate the changing relationship(s) between our conceptual boundaries and natural boundaries for these different philosophies.

Fig. 8. The relationship between natural and conceptual boundaries for different epistemologies.

Summary and conclusions

“Controversy always pounces upon the least defensible points in any position which has been advanced. We might well say that, in doing so, controversy follows a law of ‘least energy’ analogous to the well-known law of dynamics” Sellars [43: 238]. An example of this might be how opponents to strong realism, because of its socio-psychological naivety, recoil to a social constructivist position. This phenomena is observed all too often in scientific as well as philosophical debate, i.e., an argument is found lacking in some way, the focus of debate then shifts onto the lacking aspect, which is then generally used to destroy the original argument entirely. A new and often totally opposing argument is then proposed that pretends to address the shortcomings of the original argument. I am often infuriated with such unsophisticated argumentation. The method implies that there is always a better way and therefore a best way. Rather than seeing all positions as inherently wrong in an absolute sense and then seeking to synthesize a view through critical dialogue that attempts to take the ‘best of many worlds’, we often find ourselves banging our heads against a brick wall of intellectual arrogance and boorishness. In this paper I have attempted to show that even a radically realist (scientific) view of the Universe leads quite naturally to a position that frowns upon any attempts to enforce any sort of intellectual imperialism.

I have argued for the adoption of an evolutionary philosophy based upon the assumption that the Universe might be accurately described at some deep level as a CA. Though the argument is indeed based upon a strongly realist ontology it concludes that quasi-ontological pluralism must be admitted and that it is through critical dialogue that the pros and cons of different ontologies can be determined temporarily and locally. The argument given defends scientific imperialism to some extent but also attempts to make explicit science’s inherent limitations, thereby forcing us to consider the possibility of other types of knowledge being equally legitimate as a default position. It is perhaps interesting to note that despite its realist beginnings, the argument does conclude, in a sense, that anti-realism becomes the natural, initial position in any debate. Even “local triumph’s may be insufficient to provide any ground in reality for declaring one account a closer approximation of the truth” [14: 48]. However, though the default ‘universal’ position may be anti-realist in this sense, it may manifest itself in an infinitude of ways, including a return to the purely realist position if only temporarily.

One might argue that by privileging ontological pluralism and critical dialogue I am guilty of the same intellectual imperialism that I am myself critical of. To this I have no real defense²⁹, except to say that the resulting philosophy is quite empty in that no systematic framework is offered that will plug the gaps in our knowledge that result from a complex Universe. In a way, I regard the argument herein as no more than a ladder that allows one to climb to a position of philosophical emptiness that highlights the uncertainty of all things and the dangers of idolatry and reification. Once this position is reached, the ladder is thrown away and we get on with our lives. The difference being that, once ‘enlightened’ (with a small ‘e’), all our decisions and attitudes regarding what we think we know are continually treated with a healthy skepticism. We must reify to interact with the world, but we need to be fully aware that what we reify is often arbitrary and that reification is a prerequisite to our interaction with the world. Once in this position, all the tools available to us in our attempts to make sense, which includes both those tools commonly associated with complexity science³⁰, and those that are not (remembering that at some deep level any and all approaches are legitimate by default), can be selectively employed in a critical fashion.

The basis of my argument is that we can have good knowledge of the Universe without necessarily being restricted to considering only what is absolutely real. Life shows us that we can profit considerably from an ontological shift away from the ultimate reality of Life’s ‘cell states’. The scale of compression when one moves from the physical (BMP) level to the design (JPEG) level is stupendous, albeit sketchy and rough. Consider the calculations involved in a game of chess: “it is the difference between figuring out in your head what white’s most likely (best) move is versus calculating the state of a few trillion pixels through a few thousand generations” [14: 42]. But deciding what is substantially real enough to base our understanding on is inherently problematic and may take many different routes. As far as we should be concerned nothing is absolutely real and at the heart of all our philosophies, attitudes, opinions, etc. is a judgement as to what is substantially real. The distinction between what is real and what is substantially real is a subtle one, but it is such subtleties that differentiate between Capitalists, Scientists, Marxists, Religionists, as well as what makes each of us intellectually unique. These conclusions are not new. The fact that they can be derived from a strongly realist approach, however, may surprise some.

Footnotes

Acknowledgements

I would like to thank I.S.C.E. and Dr Michael Lissack for supporting the research leading to this paper and many others. Thanks also go to Caroline Richardson and Alexander Richardson for valuable diversions. This paper is a much-extended version of Richardson [39]. All papers authored by Kurt Richardson are available from http://www. kurtrichardson.com.

References

[1] D.W. Allbritton, When metaphors function as schemas: some cognitive effects of conceptual metaphors, Metaphor and Symbolic Activity 10 (1) (1995) 33–46.

[2] P.M. Allen, Economics and the science of evolutionary complex systems, SysteMexico 1 (2) (2001) 29–71.

[3] A. Backlund, The definition of system, Kybernetes 29 (4) (2000) 444–451.

[4] L.V. Bertalanffy, General System Theory: Foundations, Development, Application, George Braziller, Inc, New York, 1998.

[5] M. Bradie, Science and metaphor, Biology and Philosophy 14 (1999) 159–166.

[6] P. Callahan, Wonders of Maths: Conway’s Game of Life. http://www.math.com/students/wonders/life/life. html (accessed 2004).

[7] G. Chaitin, Randomness and Mathematical Proof, Scientific American Ccxxxii (1975) 47–52.

[8] M. Chown, Anything goes, New Scientist Magazine 158 (2137) (1998) 26.

[9] M. Chown, Before the big bang, New Scientist Magazine 166 (2241) (2000) 24.

[10] P. Cilliers, Complexity and Postmodernism—Understanding Complex Systems, Routledge, London, 1998.

[11] P. Cilliers, Boundaries, hierarchies and networks in complex systems, International Journal of Innovation Management 5 (2) (2001) 135–147.

[12] G.G. Constandache, Models of reality and reality of models, Kybernetes 29 (9/10) (2000) 1069–1077.

[13] D. Cory, The transition from na¨ive to critical realism, The Journal of Philosophy 39 (10) (1942) 261–268.

[14] D.C. Dennett, Real patterns, The Journal of Philosophy 88 (01) (1991) 27–51.

[15] B. Edmunds, Complexity and scientific modelling, Foundations of Science 5 (2000) 379–390.

[16] C. Emmeche, S. Köppe, F. Stjernfelt, Levels emergence, and three versions of downward causation, in: P.B. Andersen, C. Emmeche, N.O. Finnemann, P.V. Christiansen (Eds.), Downward Causation, Aarhus University Press, Aarhus, 2000.

[17] J.H. Fetzer, R.F. Almeder, Glossary of Epistemology/Philosophy of Science, Pergamon Press, New York, 1993.

[18] R.L. Flood, Total systems intervention (TSI): a reconstitution, Journal of the Operational Research Society 46 (1995) 174–191.

[19] A. Gottlieb, The Dream of Reason: A History of Western Philosophy from the Greeks to the Renaissance, W.W. Norton and Co., New York, 2000.

[20] J.E. Hanson, J.P. Crutchfield, Computational mechanics of cellular automata: an example, Physica D 103 (1–4) (1997) 169–189.

[21] D. Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid, Basic Books, New York, 1979.

[22] J. Horgan, The End of Science—Facing the Limits of Knowledge in the Twilight of the Scientific Age, Little, Brown and Company, London, 1996.

[23] M.C. Jackson, P. Keys, Towards a system of systems methodologies, Journal of Operational Research Society 35 (1984) 473–486.

[24] R.S. Jones, Physics as Metaphor, University of Minnesota Press, Minneapolis, 1982.

[25] C.G. Jung, Synchronicity: An Acausal Connecting Principle, Princeton University Press, Princeton, NJ, 1973.

[26] I. Kan, Open sets of diffeomorphisms having two attractors, each with an everywhere dense basin, Bulletin of the American Mathematical Society 31 (1) (1994) 68–74.

[27] G. Lakoff, M. Johnson, Metaphors We Live By, University of Chicago Press, Chicago, 1980.

[28] B. Langefors, Essays in Infology, Studentlitteratur, Lund, 1995.

[29] R.B. Laughlin, D. Pines, The theory of everything, Proceedings of the National Academy of Sciences of the United States of America 97 (1) (2000) 28–31 Available electronically from http://www.pnas.org/cgi/ reprint/97/1/28.pdf.

[30] P.R. Masani, Three modern enemies of science: materialism, existentialism, constructivism, Kybernetes 30 (3) (2001) 278–294.

[31] G. Midgley, Systemic Intervention: Philosophy, Methodology, and Practice, Kluwer/Plenum Press, New York, 2000.

[32] J. Mingers, A. Gill, Multimethodology: The Theory and Practice of Combining Management Science Methodologies, Wiley, Chichester, 1997.

[33] R.J. Moore, Dereification of Zen Buddhism, The Sociological Quarterly 36 (4) (1995) 699–723.

[34] W. Poundstone, The Recursive Universe: Cosmic Complexity and the Limits of Scientific Knowledge, William Morrow and Co, New York, 1985.

[35] H. Price, Metaphysical pluralism, The Journal of Philosophy 89 (08) (1992) 387–409.

[36] C.H. Reschke, Evolutionary perspectives on simulations of social systems, Journal of Artificial Societies and Social Simulation 4 (4) (2001) Available electronically from http://www.soc.surrey.ac.uk/JASSS/4/4/8.html.

[37] K.A. Richardson, On the status of natural boundaries: a complex systems perspective, Proceedings of the Systems in Management Seventh Annual ANZSYS Conference, 2001, 229–238.

[38] K.A. Richardson, On the limits of agent-based computer simulation: towards a nonlinear modelling culture, Proceedings of the 36th Hawaiian International Conference on System Sciences, January 7–10, 2003.

[39] K.A. Richardson, The problematization of existence: towards a philosophy of complexity, Nonlinear Dynamics, Psychology, and the Life Sciences 8 (1) (2004) 17–40.

[40] K.A. Richardson, On the relativity of recognizing the products of emergence and the nature of physical hierarchy, Conference Paper Presented at the Second Biennial International Seminar on the Philosophical, Epistemological and Methodological Implications of Complexity Theory, January 7–10th 2004, Havana, Cuba.

[41] K.A. Richardson, G. Mathieson, P. Cilliers, The theory and practice of complexity science: epistemological considerations for military operational analysis, SysteMexico 1 (1) (2000) 25–66.

[42] K.A. Richardson, P. Cilliers, M.R. Lissack, Complexity science: a gray science for the stuff in between, Emergence 3 (2) (2001) 6–18.

[43] R.W. Sellars, What is the correct interpretation of critical realism? The Journal of Philosophy 24 (9) (1927) 238–241.

[44] R.A. Shweder, A. Polytheistic, Conception of the sciences and the virtues of deep variety in: A.R. Damasio, A. Harrington, J. Kagan, B.S. McEewn, H. Moss, R. Shaikh (Eds.), Unity of Knowledge: The Convergence of Natural and Human Sciences, Annals of the New York Academy of Sciences, vol. 935 (2001).

[45] C.A. Simpkins, A. Simpkins, Simple Buddhism: A Guide to Enlightened Living, Tuttle Publishing, Boston, MA, 2000.

[46] J.C. Sommerer, E. Ott, A physical system with qualitatively uncertain dynamics, Nature 365 (9) (1993) 138–140.

[47] I. Stewart, J. Cohen, Figments of Reality, Cambridge University Press, Cambridge, 1997.

[48] M. Tegmark, Is the theory of everything merely the ultimate ensemble theory? Annals of Physics 270 (1998) 1–51. Available electronically from: http://www.hep.upenn.edu/~max/toe.pdf.

[49] J.P. van Gigch, System Design Modeling and Metamodeling, Plenum Press, New York, 1991.

[50] J.A.M. Vennix, Group Model Building: Facilitating Team Learning Using System Dynamics, Wiley, Chichester, 1996.

[51] A. Wagner, Causality in complex systems, Biology and Philosophy 14 (1999) 83–101.

[52] S. Wolfram, Undecidability and intractability in theoretical physics, Physical Review Letters 54 (8) (1985) 735–738.

[53] J. Habermas. The Philosophical Discourse of Modernity, MIT Press, Cambridge, 1987.