Complex Systems Thinking and its Implications for Policy Analysis
Kurt A. Richardson
Introduction
Aims and Background
What is complexity? A seemingly straightforward question perhaps, but as of yet no widely accepted answer is available. Given the diversity of usage it may prove useful to expand the question slightly. This can be done in a number of ways. What is complexity theory? What is complexity thinking? What are complexity studies? How is complexity measured? What is algorithmic complexity? Each of these alternative questions regards the notion of complexity in a different light. For example, according to, Badii and Politi (1997, 6) “a ‘theory of complexity’ could be viewed as a theory of modeling.” whereas Lucas (2004) suggests that a theory of complexity is concerned with the understanding of self-organization within certain types of system. Baddii and Politi therefore point towards a philosophy of science whereas Lucas points towards a set of tools for analyzing certain types of system. A special issue of the international journal Emergence (2001) contained a collection of nine papers from nine different authors, each offering their answer to the question “What is complexity science?” in nine different ways. It is often said of postmodernism that there are as many postmodernisms as there are postmodernists—the situation regarding complexity is not so different.
Depending on whose book you pick up, complexity can be “reality without the simplifying assumptions” (Allen, Boulton, Strathern, and Baldwin, 2005, 397), a collection of nonlinearly interacting parts, the study of how “wholes” emerge from “parts,” the study of systems whose descriptions are not appreciably shorter than the systems themselves (the system itself is its best model—from Chaitin’s (1999a), (1999b) definition of algorithmic complexity), a philosophy, a set of tools, a set of methodologies, a worldview, an outlook—the list is continuous.
Despite this diversity of opinion there does exist an emerging set of ideas/concepts/words/tools that do offer some approximate boundaries that delimit the field of complexity from everything else. Interestingly, the notion of incompressibility can be used to legitimate the inherent diversity within complexity, arguing that diversity (in all its forms, such as ideological, methodological, instrumental, etc.) is a feature of complexity rather than a flaw that needs to be ironed out.
The view taken in this chapter is that all that is real is inherently complex. All systems, all phenomena, are the result of complex underlying nonlinear processes, i.e., processes that involve intricate causal mechanisms that are essentially nonlinear and that feed back on each other. As will emerge in this chapter, just because every concept is defined as complex, it certainly does not follow that they all must be analyzed as if they were not simple. If the real is complex, the notion of a complex system is a particular conceptualization of the real—that wholes are comprised of nonlinearly interacting parts. To analyze these particular idealizations, a set of tools has emerged to facilitate the analyst—these tools or instruments form the science (used in a neo-reductionist sense) or theory of complex systems. The science of complexity, however, points to limits in our scientific view of complexity, and these indications can be used to construct a provisional complexity-inspired philosophy. As the real is complex (at the heart of this story is the assumption that the Universe is the only coherent complex system, or whole), then a philosophy of complexity is a general philosophy. Such a philosophy has implications for how we generate knowledge of the real, what status that knowledge has (i.e., its relationship to the real), and what role such knowledge should play in our decision-making processes.
This chapter is therefore divided into two broad sections. The first section is concerned with the science of nonlinearity, which is often regarded as synonymous with a complexity science. This will include a formal definition of a complex system, a presentation of the key characteristics of such systems, and a discussion on the analytical and planning challenges that result from the analysis of such systems. Rather than focus purely on technical detail this section will focus on the “so what?” question in regard to analysis. Section two considers the limitations of a science of complexity and briefly presents a philosophy of complexity. Such a philosophy, it will be shown, highlights the integral role of critical thinking in the analysis of the real, given that there is no such thing as an absolutely solid foundation on which to construct any knowledge claims about the real world. The philosophy of complexity developed also justifies the use of many tools and methods that are traditionally seen as beyond the scope of contemporary reductionist analysis.1 Throughout the chapter, references will be made to relevant articles that provide the details necessarily omitted.
It should be noted that this chapter is meant as a general introduction to complexity thinking rather than its specific application in the policy arena (although general indications regarding implications for analysis are given). To provide the reader with links to specific current applications of complexity in policy analysis, a short annotated list of a subset of the growing “complexity and policy analysis” literature is included towards the end of the chapter. Until recently complexity “science” was regarded more as an interesting academic discipline rather than a useful body of knowledge to assist in the analysis of practical problems. This state of affairs is quickly changing.
Themes in Complexity
Before we delve into the details of what complexity is all about, it is important to briefly explore the different versions or schools in the study of complexity.
There are at least three schools of thought that characterize the research effort directed to the investigation of complex systems, namely, the neo-reductionists, the metaphorticians, and the philosophers (Richardson and Cilliers, 2001). It should be noted that, as with any typology, there is a degree of arbitrariness in this particular division, and the different schools are by no means independent of each other.
The Neo-Reductionist School
The first theme is strongly allied with the quest for a theory of everything (TOE) in physics, i.e., an acontextual explanation for the existence of everything. This community seeks to uncover the general principles of complex systems, likened to the fundamental field equations of physics (it is likely that these two research thrusts, if successful, will eventually converge). Any such TOE, however, will be of limited value; it certainly will not provide the answers to all our questions (Richardson, 2004a). If indeed such fundamental principles do exist (they may actually tell us more about the foundations and logical structure of mathematics than the “real” world) they will likely be so abstract as to render them practically useless in the world of policy development—a decision maker would need several PhDs in physics just to make the simplest of decisions. This particular complexity community makes considerable use of computer simulation in the form of bottom-up agent-based modeling. It would be wrong to deny the power of this modeling approach, though its limits are considerable (see, e.g., Richardson, 2003), but the complexity perspective explored in the second part of this chapter suggests that the laws such nonlinear studies yield provide a basis for a modeling paradigm (or epistemology) that is considerably broader than just bottom-up simulation (the dominant tool of the neo-reductionists), or any formal mathematical/computer-based approach, for that matter.
The neo-reductionist school of complexity science is based on a seductive syllogism (Horgan, 1995):
Premise 1 There are simple sets of mathematical rules that, when followed by a computer, give rise to extremely complicated patterns.
Premise 2 The world also contains many extremely complicated patterns.
Conclusion Simple rules underlie many extremely complicated phenomena in the world, and with the help of powerful computers, scientists can root those rules out.
Though this syllogism was refuted in a paper by Oreskes, Shrader-Frechette and Belitz (1994) in which the authors warned that “verification and validation of numerical models of natural systems is impossible,” this position still dominates the neo-reductionist school of complexity. The recursive application of simple rules in bottom-up models is certainly not the only way to generate complex behavior, and so it is likely that not all observed real-world complexity can be reduced to a simple rule-based description. It does not even follow that, just because a simple rule-based model generates a particular phenomena, the real world equivalent of that particular phenomena is generated in the same way as the modeled phenomena.
Despite all the iconoclastic rhetoric about reshaping our worldview, taking us out of the age of mechanistic (linear) science and into a brave new (complex) world, many complexity theorists of this variety have actually inherited many of the assumptions of their more traditional scientific predecessors by simply changing the focus from one sort of model to another. There is no denying the power and interest surrounding the new models (e.g., agent-based simulation and genetic algorithms) proposed by the neo-reductionists, but it is still a focus on the model itself. Rather than using the linear models associated with classical reductionism, a different sort of model— nonlinear models—have become the focus. Supposedly, bad models have been replaced with good models. The language of neo-reductionism is mathematics, which is the language of traditional reductionist science—although it should be noted that neo-reductionist (nonlinear) mathematics is rather more sophisticated than traditional reductionist (linear) mathematics.
The Metaphorical School
Within the organizational science community, complexity has not only been seen as a route to a possible theory of organization, but also as a powerful metaphorical tool (see, e.g., Lissack, 1997; 1999). According to this school, the complexity perspective, with its associated language, provides a powerful lens through which to see organizations. Concepts such as connectivity, edge of chaos, far-from-equilibrium, dissipative structures, emergence, epi-static coupling, co-evolving landscapes, etc.,2 facilitate organizational scientists and the practicing policy analyst in seeing the complexity inherent in socio-technical organizations. The underlying belief is that the social world is intrinsically different from the natural world. As such, the theories of complexity, which have been developed primarily through the examination of natural systems, are not directly applicable to social systems (at least not to the practical administration of such systems), though its language may trigger some relevant insights to the behavior of the social world, which would facilitate some limited degree of control over that world. Using such a soft approach to complexity to legitimate this metaphorical approach, other theories have been imported via the “mechanism” metaphor into organization studies—a popular example being quantum mechanics (see e.g., McKelvey, 2001).
Though this discourse does not argue that new lenses through which to view organizations can be very useful (see Morgan, 1986 for an excellent example of this) the complexity lens, and the “anything goes” complexity argument for the use of metaphor has been abused somewhat. The instant concern is not with the use of metaphor per se, as it is not difficult to accept that the role of metaphor in sense making is ubiquitous and essential. Indeed, in Richardson (2005a) it is argued that in an absolute sense, all understanding can be no more or no less metaphorical in nature. However, the concern is with its use in the absence of criticism—metaphors are being imported left, right, and center, with very little attention being paid to the legitimacy of such importation. This may be regarded as a playful activity in academic circles, but if such playfulness is to be usefully applied in serious business then some rather more concrete grounding is necessary.3 Through critique our metaphors can be grounded, albeit in an imperfect way, in the perceived and evolving context.
This school of complexity, which uncritically imports ideas and perspectives via the mechanism of metaphor from a diverse range of disciplines, can be referred to as the metaphorical school, and its adherents, metaphorticians. It is the school that perhaps represents the greatest source of creativity of the three schools classified here. But as we all know, creativity on its own is not sufficient for the design and implementation of successful policy interventions.
Neo-reductionism, with its modernistic tendencies, can be seen as one extreme of the complexity spectrum, whereas metaphorism, with its atheoretical relativistic tendencies can seen as the opposing extreme. The complexity perspective (when employed to underpin a philosophical outlook) both supports and undermines these two extremes. What is needed is a middle path.
The Critical Pluralist School
The two previous schools of complexity promise either a neat package of coherent knowledge that can apparently be easily transferred into any context or an incoherent mishmash of unrelated ideas and philosophies—both of which have an important role to play in understanding and manipulating complex systems. Not only do these extremes represent overly simplistic interpretations of what might be, they also contradict some of the basic observations already made within the neo-reductionist mold; there are seeds within the neo-reductionist view of complexity that if allowed to grow, lead naturally to a broader view that encapsulates both the extremes already discussed as well as everything in between and beyond. The argument presented in the second part of this chapter makes use of these particular expressions of complexity thinking (particularly the neo-reductionist view), but focuses on the epistemological and ontological (and to some degree, ethical) consequences of assuming that the world, the universe, and everything is complex.
One of the first consequences that arises from the complexity assumption is that as individuals are less complex than the “Universe” (The Complex System), as well as many of the systems one would like to control/affect, there is no way for one to possibly experience reality in any complete sense (Cilliers, 1998, 4). One is forced to view reality through categorical frameworks that allow the individual to stumble a path through life. The critical pluralist school of complexity focuses more on what cannot be explained, rather than what can be explained—it is a concern with limits. As such, it leads to a particular attitude toward models, rather than the privileging of one sort of model over all others. And, rather than using complexity to justify an “anything goes” relativism, it highlights the importance of critical reflection in grounding our models/representations/perspectives in an evolving reality. The keywords of this school are open-mindedness and humility. Any perspective has the potential to shed light on complexity (even if it turns out to be wrong; otherwise one would not know that it was wrong), but at the same time, not every perspective is equally valid. Complexity thinking is the art of maintaining the tension between pretending one knows something and knowing one knows nothing for sure.
Nonlinear Science
The aim of this section is to provide an introduction to the science of complexity. It will introduce a loose description of a generic complex system and list some of the ways in which the behavior of such systems can be visualized and analyzed. The focus in this section is not on the technical details of bifurcation maps or phase spaces, but on answering the “so what?” question in relation to the rational analysis of such systems. Although this section is only concerned with simple nonlinear systems, most of the results can be carried forward to more complex nonlinear systems.
What is a Complexity System?
Before attempting to define a general complex system and explore its behavioral dynamics, some context is needed. The view taken in this chapter is that it is the real that is complex; every observable phenomenon is the result of intricate nonlinear causal processes between parts (which are often unseen). This view is very similar to one recently stated by Allen et al. (2005) that true complexity is “just reality without the simplifying assumptions.” Essentially, the underlying assumption is that the Universe at some deep fundamental level is well-described as some form of complex system, and that everything observed somehow emerges from that fundamental substrate. This may seem like too broad a scope, particularly when this discussion is actually concerned with the analysis of more everyday problems such as population growth or short-term financial strategy. This discourse is not intended to defend this starting point or even spell out the full implications of such an assumption. A comprehensive treatment, however, is outlined in Richardson (2004a, 2004b). Nonetheless, it is important to at least be aware of the foundational assumption for this chapter.
Everything is the result of nonlinear (complex) processes. This does not mean, however, that anything examined in detail must, without question, be treated as if it were complex. Of course, if one demands perfect (complete in every detail and valid for all time) understanding, then of course there is no choice but to account for absolutely everything—a theoretical impossibility even if one somehow managed to scrape together the phenomenal resources to complete such an undertaking; demanding absolute knowledge is demanding far more than available tools will ever deliver. All understanding is, of course, incomplete and provisional. What one finds with complex systems is that, though over lengthy timescales they may only be profitably analyzed as complex systems, one can approach them as simple systems over shorter contingent timescales. The resulting understanding will be limited, but of sufficient quality to allow informed decisions to be made and actions taken. Sufficient quality means that the model/understanding captures sufficient detail to enable prediction over timescales during which one can meet (with a greater probably of success than failure) some limited goals. Of course, sometimes a complex-type analysis is necessary and the tools of complexity science offer a conceptualization of the real that is more sensitive to the demands of understanding certain aspects of reality. The challenge is recognizing when a simple representation is sufficient and when a more comprehensive (complexity-based) analysis is necessary. Unfortunately, the real world is not so easily understood. However, this discussion will come back to the analytical implications of assuming complexity later in this section, and especially in part two. The point to make here is that simple behavior is a special case of complex behavior, and so it seems appropriate to specifically consider the characteristics of complex systems—complex systems represent the general case, not special cases.
So what is a complex system? A definition might be given as:
A complex system is comprised of a large number of non-linearly interacting non-decomposable elements. The interactivity must be such that the system cannot be reducible to two or more distinct systems, and must contain a sufficiently complex interactive mixture of causal loops to allow the system to display the behaviors characteristic of such systems (where the determination of sufficiently is problematic).
A rather circular definition, perhaps. This just goes to show how difficult it is to definitionally pin down these seemingly commonplace systems. Cilliers (1998, 3–4) offers the following description of a complex system:
- Complex systems consist of a large number of elements.
- A large number of elements are necessary, but not sufficient.
- The interaction is fairly rich.
- The interactions themselves have a number of important characteristics. First, the interactions are nonlinear.
- The interactions usually have a fairly short range.
- There are loops in the interactions.
- Complex systems are usually open systems.
- Complex systems operate under conditions far from equilibrium.
- Complex systems have a history.
- Each element in the system is ignorant of the behavior of the system as a whole; it responds only to information that is available to it locally.
The majority of the above statements are concerned primarily with the structure of a complex system—they describe constitutive or compositional complexity. In the full description offered by Cilliers (1998, 3–4) vague terminology such as “fairly rich,” “sufficiently large,” “.are usually open,” and “difficult to define” is used. Such usage is not a failure of Cilliers’s above description/ definition, but is a direct consequence of the many difficulties of pinning down a formal definition of complexity.
Statements nine and ten are of particular interest. Incompressibility, which is a technical term for the observation made in statement ten, asserts that the best representation of a complex system is the system itself and that any simplification will result in the loss of information regarding that particular system (i.e., all understanding of complex systems is inherently and inescapably limited). Statement nine basically asserts that the future of a complex system is dependent on its past. That past may be stored or memorized, at both the microscopic and macroscopic levels, at the level of the individual or the level of the whole that emerges from the interaction of these individuals.4
Statement four is the only statement above that comments specifically on the behavioral complexity of complex systems. “Non-linearity also guarantees that small causes can have large results, and vice versa” (Cilliers, 1998, 4). The next section explores the kind of dynamical behavior that can follow from nonlinearity. The key behavioral characteristics that are displayed by complex (constitutionally and behaviorally) systems are:
- Sensitivity to initial conditions—commonly referred to as deterministic chaos
- The potential for a range of qualitatively different behaviors (which can lead to stochastic chaos and catastrophes, i.e., rapid qualitative change)
- A phenomenon known as emergence, or self-organization, is displayed
Behaviors one and two can be illustrated effectively in compositionally simple systems that exhibit complex behavior. The following section, therefore, shall list a few compositionally simple systems that display the phenomena listed above. It is not possible to fully present these systems within the limitations of a single chapter, but references will be given to these systems to allow the interested reader to explore further. A longer version of this chapter is available (Richardson, 2005b) that explores such systems in much greater detail.
What is of interest is that the phenomena exhibited by such simple nonlinear systems are also exhibited by complex nonlinear systems. There are of course differences (the ability to evolve qualitatively, for example, as well as the explicit role of memory/history), but one can learn a considerable amount about complex systems by analyzing simple, but still nonlinear, systems.
What is Nonlinearity?
Before proceeding any further, it is important to clarify the meaning of nonlinearity just in case the linear-nonlinear distinction is not familiar to the reader. Figure 11.1 illustrates (a) some examples of linear relationships, and (b) some examples of nonlinear relationships. Basically, a linear relationship is where the result of some investment of time and energy is directly proportional to the effort put in, whereas in a nonlinear relationship, the rewards yielded are disproportionate to the effort put in. An important addition to this statement is that for particular contexts the relationship might actually be linear, even though, summed over all contexts, the relationship is nonlinear. This is a very important point, and again suggests that linearity (like simplicity) is a special case of nonlinearity (complexity), and that linear approaches to analysis are in fact special cases of nonlinear approaches. Mathematicians will be more than familiar with the techniques based on assuming local linearity to locally solve nonlinear problems.
When one thinks about real world relationships it is rather difficult to find linear relationships—nonlinear relationships tend to be the norm rather than the exception. The analyst must also bear in mind that it is not always obvious how to frame a particular relationship. Consider for a moment the exchange of money for goods. One might only be concerned with the monetary relationship, which in this simple scenario may well be regarded as linear given that it could be assumed that the value of the goods is the same as the value of the money. However, if one is concerned with the emotions involved in such a transaction, then there might be a situation whereby a collector has paid more than market value for an item needed to complete his/her collection. The trader might be quite pleased with making an above-market profit, whereas the collector may be ecstatic about completing a collection built over many years. It is clear that the function of the analysis determines how relationships are recognized and framed, and whether they can be approximated linearly or nonlinearly. It is safe to say that many of the problems that challenge policy analysts nowadays are characterized not only by the prevalence of nonlinearity, but also the great difficulty in recognizing what is important and what is not. The quasi-boundary-less nature of complex systems which reflects the high connectivity of the world creates some profound challenges for analysts and some fundamental limitations on just how informed decisions can be.

FIGURE 11.1 Linear versus nonlinear.
The Complex Dynamics of Systems
Simple Nonlinear Systems
There are a number of behaviors that characterize simple nonlinear systems and ways of visualizing or measuring those behaviors. The following sections briefly describe the four main behavioral characteristics of simple nonlinear systems. Rather than presenting and illustrating these behaviors in detail, the focus is on the analytical implications of these behaviors.
There are a number of very simple systems that exhibit the behaviors listed above. These include:
- the logistics map (May, 1976; Ott, 2002, 32; Auyang, 1999, 238–242);
- the Lorenz system (Lorenz, 1963; Alligood, Sauer, and Yorke, 1997, 362–365);
- a simple mechanical system-a ball moving in a double well under the influence of gravity and a sinusoidal perturbation force (Sommerer and Ott, 1993).
There are many other simple nonlinear systems that yield complex dynamics and it is advisable to explore the detailed behavior of these systems. One can only really understand the complexity and subtlety of these systems’ behaviors by interacting with them directly. There is only so much that can be gleaned from a chapter or book on the topic—complexity needs to be experienced.
There is a plethora of ways to visualize the dynamics of these systems. These visualizations include:
- time series, a simple plot of one or more variables against time;
- the phase space diagram, a plot of one system variable against one or more other system variables;
- the bifurcation diagram, a plot of all the minima and maxima of a particular time series against the value of the order parameter that generated that particular time series; the order parameter is adjusted and so the minima and maxima are plotted for a range of order parameters.
- the Lyapunov map, a map of the value of the largest Lyapunov exponent for a range of order parameter values. Lyapunov exponents (Wolf, 1986; Davies, 1999, 127–130) are a measure of divergence of two system trajectories/futures that start off very close to each other and can be used to test for chaotic behavior;
- The destination map, a plot showing the attractors to which a range of starting conditions converge; snapshots can be taken at different times to create a destination movie that shows how different basins of attraction intermingle.
Figures 11.2a and 11.2b show examples of most of these different visualization techniques. In a book format they are restricted to two dimensional representations and greyscale, but with a computer it is relatively easy to make use of a higher dimensionality. The visualization of complex high dimensional dynamics is a very active area of research, because it is through such visualization techniques that we develop an appreciation of the global dynamics of such systems.
The following several sections discuss the different phenomena that these simple nonlinear systems can display, with particular reference being made to the implications for the analysis of such systems.
Multiple Qualitatively Different Behaviors
The presence of nonlinearity, which is the norm in the real world rather than the exception, has a number of key consequences. The most important one is the potential for the same system to exhibit a range of qualitatively different behaviors depending upon how the system is initiated or how its trajectory is influenced from outside (in relation to the system of interest) forces. Constructing the phase space of any real system is no easy undertaking, simply because the abstraction process is so problematic for real world systems. However, assume for the moment that it is possible to reasonably abstract a real world system into a compositionally simple system like those listed above. The problem then becomes one of computation. A complete map of even the simplest system’s phase space requires considerable computational resources, although of course, as processing power continues on its exponential path of growth it is simply a matter of time before run-of-the-mill desktop machines can construct the phase space of compositionally simple, yet nonlinear, systems with useful degrees of accuracy.
However, one need not only focus on computational methods for the construction of phase spaces. In a sense, soft systems approaches to scenario planning, like (extended) field anomaly relaxation (Powell and Coyle, 1997; Powell, 1997) for example, are essentially indirect ways for constructing an approximate and provisional representation of a system’s phase space. Each scenario can be regarded simply as a different qualitative mode. For real life compositionally complex systems, such methods may be the only feasible way of accessing the gross features of phase space. The use of mathematics and computation are no means the only ways to construct an approximate representation of a system’s phase space.
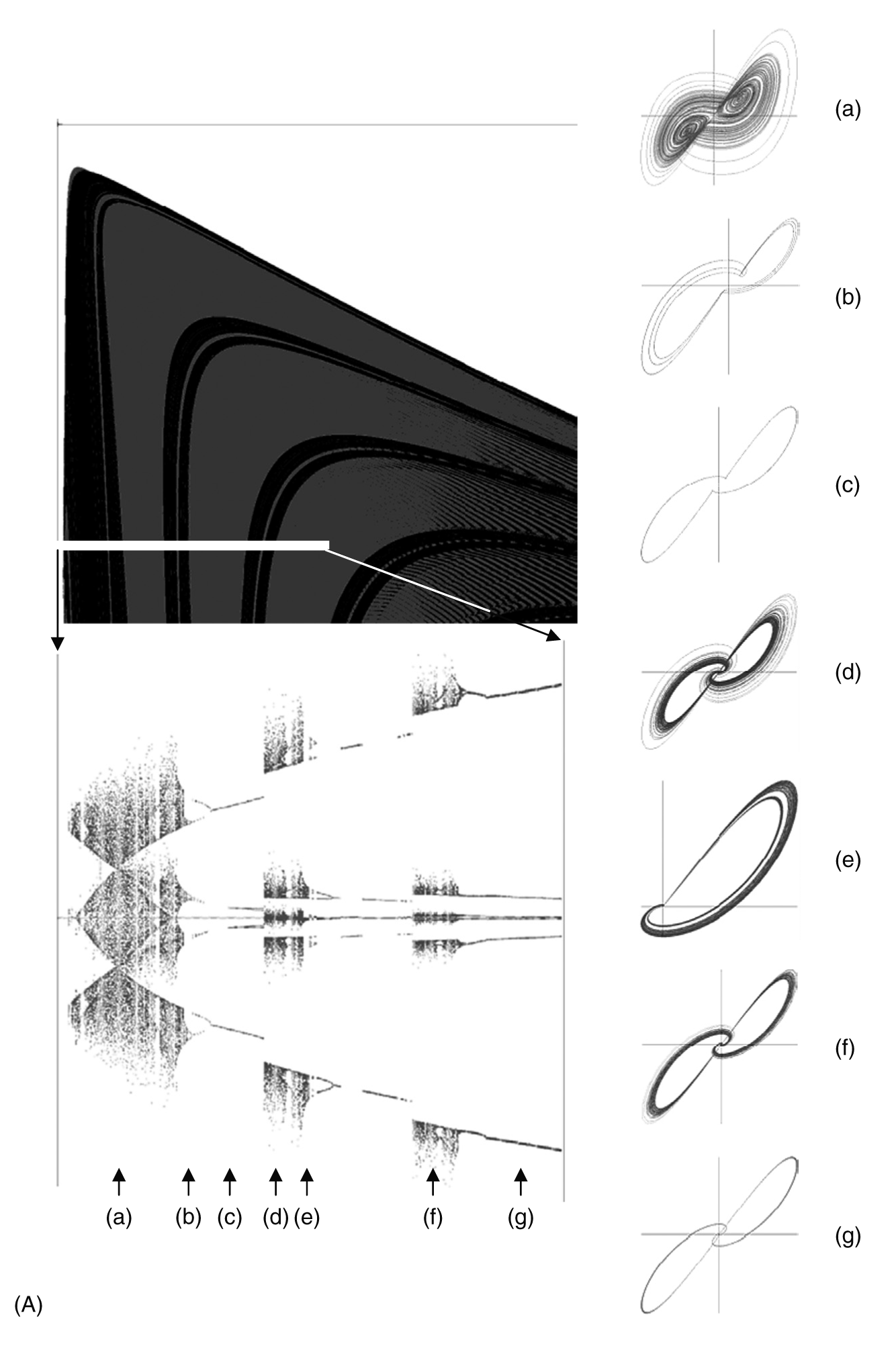

FIGURE 11.2 (A) Top-left: lyapunov map (slice) for the Lorenz system. Bottom-left: bifurcation diagram for the Lorenz system. Phase portraits (a)–(g) illustrate the different phase trajectories that different areas of the bifurcation diagram correspond to. (B) The evolution of the destination map of a simple mechanical system showing the mixing of two qualitatively different basins of attraction.
The existence of multiple modes poses challenges for the designers and implementers of policy interventions. First, multiple possibilities immediately suggest that a kind of portfolio approach to design must be taken so that the intervention strategy is effective in a number of scenarios, or basins of attraction. If policy interventions are tailored for only one attractor or encourage the system towards one particular future, then there is always the risk that even the smallest external (external to the model) perturbation(s) will knock the system into an unplanned-for mode—which is especially true for systems with riddled basins (i.e., basins that are intimately mixed with each other). Of course, these are compositionally simple systems with no adaptation, and so phase space is fixed and change only occurs in the sense that the system’s trajectory might be nudged towards a different attractor.
It might also be the case that there are a wide range of conditions that lead to the same attractor and so a solution might be found that is very robust to noise (perturbations) and, however hard one tries, the system follows the same mode persistently. This can work against the policy makers in the form of attractor lock-in, or institutionalism, in which it can be very hard to shake a system out of its existing state without it quickly “relaxing” back into familiar ways.
(Quantitative) Sensitivity to Initial Conditions—Deterministic Chaos
Deterministic chaos is mentioned a lot when presentations of complexity are made. It is not necessarily that important, and it is doubtful that any real world socio-technical system really displayed such behavior in a pure sense (because it assumes that the system representation, e.g., set of equations of motion, remain unchanged). If a system does indeed fall into a chaotic mode of operation, then quantitative prediction does become nigh impossible over extended periods of time. However, the recognition that a system is behaving chaotically is useful information, especially if this can be confirmed through the construction of the system’s “strange” attractor, or even better, a complete mapping of phase space which would show different operational modes (Lui and Richardson, 2005). If only the strange attractor is known then at least the analyst has information regarding the boundaries of the behavior, even if knowing where the system will lie between those extremes is not possible. Such information may still be used to one’s advantage—one would immediately know that mechanical predictive approaches to policy development might not be very effective at all. If a map of phase space, which would include the relationship between different possible attractors, was available, then it might be possible to identify a course of action that would nudge the system toward a more ordered attractor and away from the strange attractor.
Although long term quantitative prediction in a system behaving chaotically is not possible, this does not preclude the possibility for short-term, or local, predictions. The period over which useful predictions can be made about system behavior will vary tremendously from system to system, but short-term prediction certainly has value in the development and implementation of policy, perhaps suggesting a “punctuated equilibrium”-type approach to policy development in which each policy decision is seen as a temporary measure to be reviewed and adjusted on an ongoing basis (see McMillan, 2005; Van Eijnatten and van Galen, 2005 for examples of such evolutionary strategy development; also see the chapter by Robinson in this volume). Moreover, even though the system’s trajectory (again talking about a qualitatively static system) will never exactly repeat itself, it will often revisit areas of phase space that it has been to before. If a successful policy decision was made at the previous point in the system’s trajectory in the past, then it may well be successful again over the short term. So one can see, from the impossibility of long term quantitative prediction, that it by no means follows that various other kinds of prediction cannot be made and taken advantage of.
One note on language use; the term “chaotic system” is often used to describe systems that are behaving chaotically (bearing in mind that the term “chaos” is being used in a strict mathematical sense). However, this usage is a little misleading, as the same system will potentially have the capacity to behave non-chaotically as well. Chaos is a type of behavior, not a type of system. The systems listed above are static in that their definition/description (e.g., a set of partial differential equations) does not change in the slightest over time, new phase variables do not emerge, and the rules of interaction do not suddenly change. They can behave chaotically under certain conditions and non-chaotically under many other conditions.
Potential (Qualitative) Sensitivity to System Parameters
As mentioned in point one, there are areas of phase space whereby a well-timed external nudge may effect a qualitative change in system behavior. These areas are close to the separatrices (basin boundary) that demark different attractor basins. The closer a system trajectory draws to a separatrix, the greater the chance that small disturbances might push the trajectory into the adjacent basin (sometimes called a catastrophe, although it is not necessarily a negative development despite the name). This can be of use to policy makers, but it can equally hinder them. Any policy design (whether intentionally or not) that pushes a system trajectory close to a phase space separatrix runs the risk of failing as the system falls into another basin as a result of a modest push. Of course, the same effect can prove useful in that if it can be recognised that the system is operating near a preferred attractor basin, then a very efficient policy might be designed that provides the extra push needed for the system to adopt that preferred behavior.
There is also insensitivity to system parameters. In situations in which the system’s trajectory is moving through the middle of a basin, a large amount of effort might be required to push the system into a preferred basin of operation. Most attempts, short of overwhelming force, may likely lead to no long term change whatsoever.
There is always the possibility of instigating a deeper kind of change in which the phase space itself is redesigned and basin boundaries (separatrices) are deliberately moved around, like when a situation is created in which a new order parameter becomes relevant. However, to attempt such a move would require a deeper understanding of system dynamics than is often available to decision makers. Given the difficulties in doing such an analysis on real systems it might require an understanding that will always be beyond mere mortals.
Qualitative Unpredictability—Riddled Basins
Whereas chaotic behavior precludes long term detailed predictions, it does not preclude the possibility of making accurate qualitative predictions. The existence of riddled basins does however severely limit even gross qualitative predictions. It is still possible to make some assessment as to which qualitative modes might exist, but it is impossible to determine which modes the system will be in because it will be rapidly oscillating between different basins. Such behavior may appear to be quite random, but riddled basins are by no means random (as illustrated in Figure 11.2b).
In adaptive systems (systems whose constituent entities change qualitatively overtime—new types of entities come into being, and existing types disappear), severe limits are also placed on even long term qualitative predictions. However, it is interesting to note that even in simple systems whose ontology is permanently fixed (i.e., systems for which their definition/composition does not qualitatively change) can display qualitative unpredictability.
Though the situation for ontologically (compositionally) changing systems is more complex, in that prediction becomes even more problematic than for the simple systems described thus far, such changeable systems may still be effectively reduced and represented as simple systems, albeit temporarily and provisionally. One of the key observations of complexity theorists is the highly problematic nature of the abstraction process.
Complex Nonlinear (Discrete) Systems—Networks
Having considered the different behavioral characteristics of compositionally simple systems, it is time to look at compositionally complex systems. Interestingly, all the observations made in relation to the behaviors that can result from nonlinearity in simple systems can be extended almost without change to compositionally complex systems or networks. Complex networks also exhibit a phenomenon referred to as emergence, of which self-organization is an example. However, before moving on to consider network dynamics it is important to first consider the structure, or topology, of various networks, as there are a range of analyses available to policy makers even before they need concern themselves with network dynamics.
The following list provides some areas of interest when considering the structure of complex networks:
- Network topology exists in classifications such as ordered/regular, small-world (Watts and Strogatz, 1998), scale-free (Barabási and Albert, 1999), and random (Erdős and Rényi, 1959). It turns out, thus far at least, that there are four broad network types when we consider structure only. Of the four it is found that many natural and socio-technical systems are actually scale-free networks, which means that they contain a few nodes that are very well connected and many nodes that are not highly connected (see e.g., Adamic, 1999 for an analysis of the World Wide Web)
- Cluster co-efficient is a measure that indicates how “cliquey” a network is, or how many subgroups are contained within the same network.
- Path length is the shortest route between two nodes. In large networks it is found that the average path length is surprisingly low. For example, in Yook, Jeong, and Barabási (2001) the authors considered a subset of the Internet containing up to 6,209 nodes. The average path length was found to be only 3.76; to go from any node in the network to any other one requires no more than 4 steps on average
- Degree distribution provides information concerning the distribution of nodes with particular densities of connections. Either the number of in-connections (indegree) or out-connections (outdegree) can be considered. It is through the plotting of such distributions that it is possible to determine if a particular network is regular, small-world, scale-free or random.
- Feedback loops refers to the number and size of feedback loops comprising a particular network. Different networks containing the same number of nodes but having quite different topologies can have very different feedback profiles.
- Structural robustness refers to how connectivity parameters, such as average path length and average cluster size, deteriorate as connections or nodes are randomly removed. Some network topologies are more robust than others. For example, if connections are removed at random, then a scale-free network tends to be more robust than a random network. However, if nodes are removed in order of number of connections then random networks are rather more robust than scale-free networks.
Lessons from Structural Considerations
Although not exactly an acknowledged subfield of complex dynamical systems theory, network theory does provide a range of analytical tools and concepts that can be usefully brought to bear on understanding the dynamics of such systems—and it should be noted that structure and dynamics are anything but independent. In dynamical systems there is a complex interplay between structure and dynamics that is barely considered at all in current network theories. However, having information about network characteristics such as path length, clustering, and structural robustness do offer potentially useful understanding (such as the identification of potent/impotent nodes), which could be used to support particular types of connectivity-based interventions.
Of course there are severe limitations to such an analysis, the first being the considerable challenges of even constructing an accurate network representation of a real system in the first place. Construction of such a map cannot occur without a purpose, otherwise one would simply end up with a network in which every node was connected to every other node. To apply these approaches usefully, the analyst must decide which types of interconnections need to be represented in the network model. For example, the analyst might only be concerned with financial transactions in which case a connection exists between two nodes that exchange money, or certain types of goods. Simply asking how a particular system is connected is a pointless question. To a great extent the intervention strategies available to policy makers will determine the sorts of questions that can be asked and therefore the type of network representation that can usefully be constructed. What sort of network representations would contain the World Trade Center as a dense node, for example? Whichever map is constructed, it is important to note that it is not an accurate representation of the real world network but a particularly bias abstracted slice through that network. As such, there is much more unaccounted for than there is accounted for.
Even if a usefully representative network map can be constructed, it can be no more than a static snapshot. This need not deny it of its usefulness, but the analyst must consider the timescales over which such a snapshot will remain valid and therefore useful. Real network/systems evolve over time—the connections change, new nodes appear, existing nodes disappear or change their rules of interaction (through learning for example), etc., and so static network models cannot avoid being limited in their validity (like any model one can possibly construct of any real world phenomena, this is not a problem particular to network models!).
Lastly, and most obviously, there is no way to explore the dynamics of a real world system through such limited network analyses. There is no way to confidently understand the form of the relationship between connecting nodes, no way to understand how the various feedback loops interact, no way to construct a phase portrait of such a system to understand its qualitatively different modes of operation. One cannot even be sure that the highly connected nodes have the majority of the control/influence except as the result of a superficial first order approximation. In dynamical systems, a low-connected node can have widespread influence because of the multiple paths to every other node. However, such multi-order influence is far harder to consider without detailed simulation than the often overwhelming first-order control exhibited by dense nodes. Even then, following causal processes is by no means a trivial undertaking.
For further details on the statistical properties of complex networks please refer to Albert and Barabási (2002). For a more accessible general introduction to networks refer to Barabási (2002). To explore further how network analysis can lead to a better understanding of how organizations function, Cross and Parker’s The Hidden Power of Social Networks (2004) may prove useful. This book also contains a detailed appendix on how to conduct and interpret a social network analysis.
Bringing Networks to Life
Of course, just because a system has a networked structure, it certainly does not follow that it is a complex system—computers are examples of very complicated networks and yet one would not consider them as complex systems (despite the fact that each node—transistor—responds nonlinearly). In the networks discussed in the previous section, the only concern was whether or not a relationship, or “edge”, exists between two nodes. The nature of that relationship has not yet been discussed. If the relationship is a linear one then the overall behavior of the system will be rather trivial. Such a system is often referred to as a complicated system as opposed to a complex system. However, as already suggested above, just because linearity does not lead to any particularly interesting behavior, nonlinearity by no means guarantees chaos, multiple attractor basins, self-organization, etc. Nonlinearity, though is a minimum requirement (although it is by no means a requirement that is particularly hard to fulfill in the real world).
In the following sections, dynamic networks containing nonlinear relationships, namely, complex systems, will be explored. As an example of a simple complex system we shall consider Boolean networks. For a treatment of Boolean networks, please refer to Boosomaier and Green (2000), (30–32) or Kauffman (1993, especially chap. 5), but basically, these networks are comprised of a number of nodes that can only take on one of two possible binary states. The way in which each node evolves, or the state its nodes adopt as time is stepped forward, is dependent upon how each node is connected to its neighbors—both by number of connections and how those connections are processed. The relationship between behavior and structure for any one particular network will depend on a complex interplay between the network connectivity and the details of each of those connections.
With potentially thousands of multi-dimensional nodes (in more sophisticated versions of the Boolean model) it becomes a nontrivial exercise to extract meaningful (emergent) patterns. The space-time diagram (which shows the state of each node over time) is a useful way to visualize the dynamics of Boolean networks, but even here the extraction of patterns can become very difficult indeed. Constructing the phase space of complex systems offers another way to get a handle on a particular system’s overall dynamical behavior, but again, the computational resources needed to obtain an accurate representation become prohibitive for even modestly sized networks.
As mentioned above, finding different ways to visualize the dynamics of such high-dimensional systems is a real challenge and a very active area of research in complex systems. Ultimately, the rich dynamics of the system need to be reduced, through aggregation or some other means for them to be appreciated/interpreted to any degree. Such reduction removes detail for the sake of clarity, and must be handled with great care.
Phase Space for Dynamical Boolean Networks
Figure 11.3 is a complete representation of a particular Boolean network’s phase space. It includes all transient information, namely, information regarding system’s trajectories before they converge on a particular attractor, as well as attractor information. It is for this reason that it looks quite different from the phase space depicted in Figure 11.2A. In Figure 11.2A (a–g) all the paths to the attractor basins have been suppressed. Another way to visualize the phase space of a Boolean network is to color each point in phase space to correspond with the attractor that it fi y converges on. This has been done in Figure 11.4. Figure 11.4 is equivalent to the phase portrait, for a continuous system, shown in Figure 11.2A (main image). Although the image does not look too good in greyscale, it is clear that there is structure there; the form of confi of a particular shade (which correspond to a particular attractor basin) are certainly not distributed randomly. The phase space image of the Boolean network does seem to be rather more complex than that of the continuous system shown in Figure 11.2A. This is perhaps no surprise, as the Boolean network is very much more (compositionally) complex than the simple continuous system.
Chaos in Boolean Networks
As the phase spaces of discrete Boolean networks are finite, there really is no behavioral equivalent to chaos as all initial conditions will eventually fall onto a cyclic attractor. Not all cycles are created equal and quasi-chaotic behavior does indeed occur, which can be equated with the chaos exhibited in some continuous systems. The phase space of some Boolean networks contains cyclic attractors that have periods much larger than the size of the network. Attractors or periods much greater than network size are examples of quasi-chaotic behavior in discrete Boolean systems.

FIGURE 11.3 The complete phase space of a particular random network. The phase space is characterized as 2p1, 1p2, 1p5, 1p12, 1p25, 1p36 (XpY: X number of attractors with period Y)—a total of seven basins of attraction.
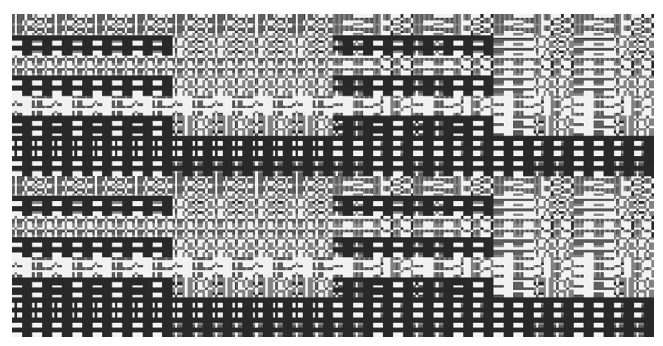
FIGURE 11.4 An example of the phase space of a simple Boolean network (note that Figure 11.3 and Figure 11.4 show data from two different networks).
If one continues with this idea that chaotic behavior is no more than very complex dynamics then there are several ways in which these systems’ behaviors can be characterized in terms of:
- Transient length—larger networks can have astronomically long transients before an attractor is reached, which sometimes look as though the system is behaving chaotically, although it might eventually converge on a point attractor
- Long cycle periods—it is quite possible that chaotic behavior might simply be the result of cyclic attractors with astronomically long periods as is easily found in large discrete networks
- Number of attractors—on average, the number of attractors in discrete Boolean networks of the sort discussed above grows linearly with the network size, N (Bilke and Sjunnesson, 2001)
These three aspects of dynamics each provide a different way of viewing a system’s dynamics as complex or not and should not be used in isolation from each other. For example, a system characterized by only one attractor may still exhibit astronomically long transient paths to that particular attractor, which would mean that the exclusion of transient data in developing an intervention would be inappropriate.
The existence of multiple attractors in phase space and the nontrivial way in which phase space is often connected leads us to another type of robustness: dynamical robustness.
Dynamical Robustness
Whereas structural or topological, robustness is primarily concerned with the spatial connectivity of networks, dynamical robustness is concerned with the connectivity of phase space itself. Dynamical robustness is concerned with the probability that a system can be nudged from one basin into another by small external perturbations.
One would expect that on average, systems with large numbers of phase space attractors would have lower dynamical robustness than systems with lower numbers of phase space attractor as there is a direct relationship between dynamical robustness and number of attractors. However, the size of the basins associated with different attractors are often different, as is the connectivity of phase space, and so dynamical robustness also contains the influence of these two contributions as well as the number of attractors.
The reason that dynamical robustness is of interest (and there are a number of ways to define it), is so that an analyst can get a feel (and it is not much more than that) for how stable a proposed solution might be. If the dynamical robustness of a solution is relatively low then we can readily assume that the chances that small perturbations will cause the system to deviate for our desired state are quite high. Richardson (2004c, 2005c) explores the impact of removing supposed organizational waste on the organization’s dynamical robustness. It is found that as waste is removed, there is a tendency for the system to become less stable. This new found buffering role for supposed waste has significant implications for policy interventions that attempt to make the target organizations more efficient by making them leaner, in a sense.
The previous sections have introduced a number of tools, measures and definitions for understanding the behavior of complex (dynamical) systems. However, there is one area that has not been discussed, which is odd given that nearly all the literature of complex systems makes discussion of this particular concept central. This concept is called emergence. The reason it has not been discussed at length thus far is that it is a particularly slippery term that is not easily defined, much like complexity itself. The next section summarizes the key features of what the term emergence might refer to.
What is Emergence?
This brief discussion of emergence is not intended to be a thorough investigation. The interested reader may find Richardson (2004a) a useful discussion. The notion of emergence is often trivialized with statements such as “order emerges from chaos” or “molecules emerge from atoms” or “the macro emerges from the micro.” It is quickly becoming an all or nothing concept, particularly in management science. The aforementioned paper explores how the products of emergence are recognized and their relationship with their “parts.” The following statements summarize the argument offered therein:
- Emergent products appear as the result of a well-chosen filter—rather than the products of emergence showing themselves, we learn to see them. The distinction between macro and micro is therefore linked to our choice of filter.
- Determining what “macro” is depends upon choice of perspective (which is driven by purpose) and also what one considers as “micro” (which is also chosen via the application of a filter).
- Emergent products are not real, although “their salience as real things is considerable.” (Dennett, 1991, 40). Following, Emmeche, Köppe, and Stjernfelt (2000) we say that they are substantially real. This a subtle point, but an important one, and relates to the fact that the products of emergence, which result from applying an appropriate filter—theory, perspective, metaphor, etc.—do not offer a complete representation of the level from which they emerged.
- Emergent products are novel in terms of the micro-description, that is, they are newly recognized. The discussion of emergent products requires a change in language—a macro-language—and this language cannot be expressed in terms of the micro-language.
- In absolute terms, what remains after filtering (the “foreground”) is not ontologically different from what was filtered out (the “background”). What is interesting is that what remains after a filter is applied is what is often referred to as the real, and that which has been removed is regarded as unimportant.
- The products of emergence and their intrinsic characteristics, occurring at a particular level of abstraction, do not occur independently—rather than individual quasi-objects emerging independently, a whole set of quasi-objects emerge together.
- The emergent entities at one level cannot be derived purely from the entities comprising the level beneath, except only in idealized systems. What this means is that molecules do not emerge from atoms because atoms do not provide a complete basis from which to derive molecules (as atoms are emergent products of another level, and thus they are only partially representative). In this sense the whole is not greater than the sum of its parts because the parts are not sufficient to lead to the whole.
- Emergent products are non-real yet substantially real, incomplete yet representative.
- All filters, at the universal level, are equally valid, although certain filters may dominate in particular contexts. In other words, there is no universally best way to recognize emergence, although not all filters lead to equally useful understanding; although there is no one way to see things, it does not follow that all ways of seeing things are legitimate.
The bullets above might seem rather philosophical for a chapter on policy analysis. Other than the slippery nature of the term itself, there are other reasons to approach the discussion in this way. The language used thus far in this chapter has been rather positivistic in nature, which might inadvertently encourage some readers to assume that the tools and measures presented could be used in a systematic way to assist in the development of interventions in complex systems. This is certainly not the case. Intervening in complex systems is highly problematic and although there are opportunities for rational action the inherent limitations that arise from the problematic nature of activities such as problem bounding, system modeling, prediction and interpretation should not be overlooked. This philosophical attitude will be discussed further in the second part of this chapter. For now, it will suffice to suggest that the role of thinking critically about ideas and concepts is central to any complexity-inspired policy analysis—complexity science offers not only new tools, but also a particular attitude toward all tools.
The examples used thus far in this chapter—the simple nonlinear systems and the Boolean networks—may seem to some to be overly simplistic in their construction and therefore irrelevant to real-world policy analysis. The next section will extend the idea of complex systems to include complex adaptive systems that are more readily associated with real world social systems. It should be noted, however, that considering more complex (both topologically and dynamically) systems does not invalidate what has been said already. The interesting thing about nonlinearity is that most of what can be learned from simpler nonlinear systems can be readily applied to more complex systems as long as an awareness of their contextual dependencies is present. For example, we can readily construct the phase space of an adaptive system by making the simplifying assumption that what we have constructed is a snapshot that at some point (not necessarily in the not too distant future) will need to be updated.
There are very few, if any, universal principles in complexity theory (except perhaps that one!) that would hold for all systems in all contexts. However, there will often be contexts in one system for which results obtained through the study of another system will be applicable. There will not be a one-to-one mapping, but results are transportable even if only in a limited way. For this reason, the study of systems as seemingly trivial as Boolean networks can teach us a lot about more complex systems. Even the study of linear systems is not necessarily redundant.
From Boolean Networks to Agent-Based Models
Boolean networks are clearly relatively simple complex systems; they are less complex than agent-based models, and certainly less complex than reality. Their structure is static, as are the nodes’ interrelationships. However, despite their simplicity, useful observations and analyses can be made that may be relevant for systems as potentially complex as real world socio-technical organizations, such as the multi-faceted role of waste, for example. There will be increased dimensionality with systems containing more complex nodes, or agents, whose interrelationships change with time and circumstance. For example, agent-based modeling is often seen as the state-of-the-art when it comes to complex systems modeling. Agent-based models are simply more complex Boolean networks, like the ones already discussed. (For examples of the agent-based modeling approach in policy analysis please refer to Lempert, 2002a; Bonabeau, 2002). The key difference is simply that the rules that define each agent’s behavior are often more intricate than the simple rule tables for Boolean networks. The way in which agents interact is more context-dependent, and the underlying rules may actually evolve over time (as a result of a learning process for example—although there may be meta-rules that guide this process too). The state of any given agent will also be less restrictive than the two-state Boolean agents, and require greater dimensionality to describe it. Despite these differences, the basic observations made above still hold. The visualization techniques above still provide useful ways to explore the system’s global dynamics, although the dimensionality of such constructions will be greater and will almost certainly evolve over time.
Peter Allen of the United Kingdom-based Complexity Society has developed a typology of models that is based upon increased model complexity, which is useful is helping us understand the relationship between different model types.
Computer Model Types
When developing computer-based models of organizations, four modeling types are generally used. These are equilibrium models, system dynamics models, self-organizing models, and evolutionary models. The differences between these modeling approaches are the assumptions made to reduce the complex observed reality to a simpler and therefore manageable representation. According to Allen (1994, 5) the two main assumptions (or, simplifications) made are:
- Microscopic events occur at their average rate, average densities are correct
- Individuals of a given type, x say, are identical
Essentially, these assumptions restrict the capacity of any modeled system to macroscopically or microscopically adapt to its environment. In some cases, assumption two is relaxed somewhat, and diversity in the form of some normal distribution is allowed. Combinations of these assumptions lead to different models. In addition to the above assumptions, another one is often made— that is that the system sufficiently rapidly achieves equilibrium. So, in addition to the model not being able to adapt macroscopically or microscopically, equilibrium is also achieved. The attraction of equilibrium modeling is the simplicity that results from only having to consider simultaneous and not dynamic equations. Equilibrium also seems to offer the possibility of looking at a decision or policy in terms of a stationary state before and after the decision. This is a dangerous illusion, although it does not deny that, as long as great care is taken, equilibrium models may provide useful, albeit very limited, understanding of complex systems.
Of course, if the assumptions imposed were true for a restricted (in time and space) context then the equilibrium model would be perfectly acceptable. What is found, however, is that in real organizations, none of these assumptions are true for any significant length of time. So, although the equilibrium model offers only a single possibility—that of equilibrium—it omits all the other possibilities that may result from relaxing one’s modeling assumptions.
The following bullets list the different models that results when different combinations of these assumptions are relaxed. Adjustments to the simple Boolean network model used earlier are also suggested that would turn them into the different sorts of models listed.
- Making assumptions one and two yields the nonlinear system dynamics model; discrete Boolean networks are examples of simple nonlinear system dynamics models—once they are initiated they move to one particular attractor and stay there even though the system’s phase space may be characterized by many attractor basins. For these networks, the interconnections remain the same (i.e., topology is static) and the transition rules are also fixed.
- Making assumption two yields the self-organizing model; if one incorporated into each Boolean node a script that directed it to switch state (regardless of what the rule table said) under particular external circumstances (noting that the standard Boolean network is closed), then the system could move into different basins depending on different external contextual factors. Such an implementation could simply be that a random number generator represents environmental conditions and that for particular ranges of this random number a node would ignore its rule table and change state regardless.
- Making neither assumption yields the evolutionary model; for an evolutionary Boolean network, the network topology would change and the rule tables for each node would also change. A set of meta-rules could be developed for each node that indicate the local conditions under which a connection is removed or added and how the rules would evolve—it is quite reasonable for these rules to be sophisticated in that they could include, and rely on, local memories. Another set of rules could determine when new nodes are created and how their connections and rule tables are initiated. This is essentially what the agent-based modeling approach is. This model is not truly evolutionary as we have simply created a set of meta-rules to direct change within the system. However, if we take evolutionary in such a literal way then no model can ever really be evolutionary.
Now that a summary of complexity science has been presented, some comments can be made regarding one’s ability to rationally design interventions to achieve certain preset aims.
What are the Implications for Rational Intervention (Control) in Complex Networks?
Assuming that accurate representations of real world complex systems can be constructed, then what is the basis for rational intervention in such systems? If we assume that everything is connected to everything else (which is not an unreasonable assumption) and that such systems are sensitive to initial conditions (at the mercy of every minute perturbation) then, indeed, there would seem to be little basis for rational intervention. To take these assumptions seriously we would have to model wholes only, or, extend our modeling boundaries to the point at which no further connections could be found. This is more than an argument for wholes, and is really an argument that suggests that to be rational in any complete sense of the word, one must model the Universe as a whole. This is the holistic position taken to an absurd extreme. What is interesting is that from a complex systems perspective, no member of a complex system can possibly have such complete knowledge (point ten in the section titled “What is a Complexity System?”) Even if we could find wholes other than the entire Universe then the sensitivity to any small external perturbation would undo any efforts to intervene in a rationally designed way. Hopefully, the discussion presented thus far provides ample evidence to support the dismissal of such a pessimistic and radically holist position—holism is not the solution to complexity.
As we have already seen, despite all the change in complex systems, there are many stabilities that can be identified and that can also provide a basis for rational intervention. First of all, one needs to recognize that asking for a basis for rational intervention does not mean absolute rationality. It means a bounded (Simon, 1945, 88–89; see the Mingus chapter in this volume) and temporary rationality, which has considerable limitations to it.
For example, if one is confident that a system dynamics-type representation of a real world system has merit, then identification of qualitatively different operating scenarios that would allow the development of policy strategies that succeed in a variety of future possibilities would be feasible. Another way of saying this is that it would be possible to develop a policy that was sensitive to a number of contextual archetypes. Possibilities that are known but could not easily be designed for might be dealt with as part of a risk assessment, and possibilities (unknown) outside the bounds of the model might be dealt with through contingency planning.
If a self-organizing model turned out to be appropriate then one could not only identify different possible operating scenarios, but also relevant elements, i.e., the elements/entities/nodes that are primarily responsible for the overall qualitative variation in the system. rom such a reduced representation one has the possibility of more efficiently re-directing a system towards preferred futures. One can also get a handle on how robust solutions might be, and how one might allocate resources to achieve preferred policy aims.
Even if dynamical models are not used, one can construct static network representations that make available a wealth of other analytical techniques that would allow the assessment of topological characteristics such a path lengths, structural robustness, the presence of dense nodes, etc. that provide potentially useful information when it comes to developing intervention strategies.
It is clear that just because a system of interest is complex, it does not follow that analysts are necessarily impotent when it comes to developing robust intervention strategies. Although there are many possibilities for understanding certain aspects of complex systems, there are also important limitations to our ability to understand such systems. As one example in complex systems, it is often the case that there is a delay between a particular cause and an observable effect—this delay can be such that it becomes very difficult indeed to associate a particular cause with a particular effect. Particular effects can have multiple causes (a phenomenon known as equifinality). This can work in one’s favor, as there may be a number of ways to achieve the same goals. However, it is also a disadvantage in that there will likely be many ways to derail a particular strategy. Intervening in complex systems often changes them in nontrivial and unforeseen ways, which are difficult to account for in analyses. New entities/players/species also emerge that are near impossible to predict that can totally change the phase space. Sometimes it can very much seem like trying to pin the tail on a fast moving donkey. Cilliers (2000a, 2000b) discusses the limits of understanding concerning complex systems in greater detail.
Although there are many tools and concepts available to assist in the understanding of complex systems and inform policymaking, it is also apparent that we need a strategy for managing the limits to what we can know about them. A naïve realism that is overly confident in one’s ability to represent complex systems is inappropriate regardless of how many analytical tools are developed to deal with complexity head-on.
Complexity theory can be used to help us understand the limits placed on developing knowledge of those same systems. For example, if one assumes that the real world system of interest is indeed a complex system (bearing in mind that the presupposed assumption is that all phenomena are the result of complex nonlinear processes) then what is the status of the resulting model of that system—even if it is a complex systems model—given that such a model will necessarily be an abstraction?5 Focusing on the phenomenon of interest for a moment, if the boundaries inferred from perceptions of reality to form a model are a little bit off, or the representation of nonlinear interactions are inaccurate—even if only slightly—then there is always the possibility that the understanding developed from such a model is wholly inadequate because small mismatches can have serious consequences. Even a model that accounts for all observable data is still not out of the woods. Given that nonlinear processes are operating at all scales, there is an infinite number of ways to build a model that generates what has already been seen (Richardson, 2003), and so one can never be sure that the model explains observables that have not yet been observed; applying the results of a model outside of the context in which it was developed is highly problematic. Another source of error, which is related to the first, is that all boundaries, or stable patterns, in a complex system are emergent, critically organized, and therefore temporary (and as already seen, they are not even real in any absolute sense but are the artifacts resulting from a filtering process).
Given these difficulties in even constructing a useful model in the first place—modeling certainly is not as straightforward as map-making traditionally is, which is what modeling really is in the mechanistic view of the world, it is essential to have a theory of limits. Such an understanding informs a philosophy of analysis and this will be the focus for the second part of this chapter.
Towards an Analytical Philosophy of Complexity
In the previous section it was suggested that complexity offers more than just a set of new tools—it also suggests a particular critical attitude toward all our instruments of understanding and the status of the understanding that those instruments give. Naively employing any of the tools of complexity in an unquestioning, unsophisticated way, without concern for their limitations, is little better than denying complexity in the first place. Complexity-based, or complexity-informed, analysis is as much to do with how analytical tools are used as it is to do with which tools are used.
The aim of the proceeding short section is to explore the philosophical implications of assuming that all real systems are complex or the result of underlying complex (nonlinear) processes. As mentioned above, just because all phenomena/systems are the result of complex, nonlinear processes it does not follow that simple, linear models are obsolete—aspects of complex systems can indeed be modeled as if they were simple, even if only approximately and temporarily. The result of acknowledging the inherent complexity of the real is a tentative critical philosophy of analysis. The exploration begins with probably one of the most fundamental questions: What does it means to exist? In complexity terms this can be rephrased as “When is a pattern a real pattern?” or “When is a boundary a real boundary?” A major part of the process of analysis is the extraction of stable patterns, and so understanding the status of patterns in complex systems is key to developing an analytical philosophy to understand them.
On the Nature of Boundaries
In Richardson (2004b) a detailed analysis is provided regarding the status of boundaries in a complex system, i.e., the emergence of objects and their ontological status. These arguments are summarized here.
The basic conclusion that the complexity-based argument given thus far leads to is that there are no real boundaries in any absolute sense (this by no way suggests that in certain instances assuming the existence of particular boundaries is inappropriate). How are we to derive knowledge of particular systems then (particular if no systems really exist)? This state of affairs is not as dire as it might immediately seem. There is no need to follow the radical holists to model the world, the universe and everything. From a complexity perspective, although there may be no real boundaries, there are resilient and relatively stable emergent structures, or patterns. In fact, there is a distribution of boundary stabilities. No evidence is given for what this distribution may actually be (the theory of self-organized criticality from [Bak, 1996] might suggest that such a distribution is in fact scale-free); it is simply argued that there is a distribution. Figure 11.5 illustrates a possible stability distribution (which has no theoretical or empirical basis).
At one end of the stability spectrum there are boundaries/structures/patterns that are so persistent and stable that for most intents and purposes it can safely be assumed that they are in fact real and absolute. Boundaries that delimit the objects of science-based technology exist toward this end of the spectrum. Such long-term stability allows a “community of enquirers,” for example, the scientific community, to inter-subjectively converge on some agreed principles that might actually be tested through experiment. Under such conditions it is quite possible to develop quasi-objective knowledge, which for most intents and purposes (but not ultimately) is absolute. The existence of such persistent boundaries allows for a something other than a radically holistic analysis—this may explain why the scientific program has been in many ways so successful when it comes to technological matters. In many circumstances reductionism is a perfectly valid, though still approximate, route to understanding complex systems. In short, what is suggested here is that scientific study depends upon the assumption that natural boundaries are static (in a qualitative sense), and that if one can prove that the boundaries of interest are in fact stable and persistent, then scientific methods, even reductionist methods, are more than adequate means to understand and interact with them.

FIGURE 11.5 A possible distribution of natural boundary (structure) stability.
At the other end of the stability spectrum is essentially noise in which the lifetime of apparent boundaries might be so fleeting as to render them unrecognizable as such and therefore unanalyzable. Under such circumstances, attempts to develop knowledge are strongly determined by the whims of the individual, with observed boundaries being more a function of our thirst to make sense, rather than an actual feature of reality. To maintain a purely positivistic position (i.e., a position that strives to attain absolute, complete, and unbiased understanding, and assumes that something called the scientific method is the route to such understanding), one would have to accept a radical holism and consider the entire universe (as the only way to have such perfect understanding is to model it all) a practical absurdity and a theoretical impossibility as has already been suggested. This is the only method by which a robust understanding could possibly be derived.
Fortunately, a vast majority of the perceived Universe is not quite so nebulous. This does not mean, however, that boundary recognition and allocation is a trivial exercise. In fact, without the ability to not only determine the stability distribution, but also recognize where the objects of interest exist on the curve, it is very difficult to determine how to approach them. Radical positivists might argue that a rigorous implementation of the scientific method is appropriate across the board though such broad-brush positivism seems quite the opposite. It is likely that the social, or soft, sciences with their willingness to work with a plurality of (possibly incommensurable) methods and perspectives is better suited to deal with a state of affairs in which boundary recognition and allocation is deeply problematic. This position reflects Cilliers (2001, 142) concern that “[i]n accepting the complexity of the boundaries of complex systems, we are committed to be critical about how we use the notion since it affects our understanding of such systems, and influences the way in which we deal with them.”
Complexity and Philosophy
Because boundaries are both emergent and temporary and their recognition is problematic, the need for critical thinking and paradigm/perspective/methodological pluralism comes to the forefront. If there is no basis from which to unambiguously determine the best way to frame our models, then the importance of approaching the same problem from multiple directions becomes plainly apparent. If the validity of the understanding derived from one’s models is potentially critically sensitive to the underlying assumptions, then the importance of critically refl on those assumptions also becomes equally apparent. So, in short, assuming that all phenomena are the result of complex nonlinear processes, causes one to recognize the central importance of both criticism and pluralism in analysis.
Justifying Pluralism
The first step in making an argument for a pluralist analytical philosophy is to justify pluralism (both ontological and epistemological/methodological). To some degree this has already been accomplished by highlighting the ambiguity of pattern recognition in complex systems, i.e., the considerable difficulties in recognizing an object as an object. The perception of the objects that form the basis of our models appear as a result of a filtering process, in other words, the objects of perceived reality are what is left over when a lot of background noise has been removed. The determination of what is the background and what actually is noise is a characteristic of the filter chosen. We say that these resulting (quasi-)objects are substantially real to make explicit the fact that there is a subjective element in their recognition, which necessarily changes the way in which we use them—if we assume their existence is objective and absolute then there is no reason to think about them critically and no reason to consider using different filtering processes.
Assuming an acceptance of pluralism as a key element of a philosophy of analysis, all the tools and concepts discussed in the previous section are of a particular sort—they are based on mathematical ideas and constructs. Even accepting that there are many ways to build a model of the same phenomenon, the tendency is still towards formal mathematical approaches and away from softer, seemingly less formal, approaches. However, in assuming pluralism, the restriction to mathematical approaches is an additional arbitrary assumption and what can be considered as a case of horizontal pluralism rather than pluralism in its truest sense. Here it can be seen that mathematical approaches to complexity offer evidence that mathematical approaches are not necessarily the only, or best, way to manage complexity—this comes from the recognition that mathematics itself is not capable of explaining all there is to know about complexity.
Horizontal and Vertical Pluralism
Even though the above view has the capacity to allow the exploration of the same phenomena from different perspectives, all the perspectives are scientific, or mathematical, in nature. This view is exemplified by W.V. Quine’s brand of ontological relativism: “Here the plurality consists in the possible existence of a range of alternative scientific worldviews, each empirically adequate to more or less the same degree, and none, even in principle, have privileged claim to provide a ‘truer’ description of the world” (Price, 1992, 389). Even “incompatible theories can explain the same facts equally well and make equally good predictions” (Masani, 2001, 279). Price (1992) goes on to argue that
[t]here may be equally valid possible scientific worldviews, but all of them are scientific worldviews, and in that sense are on the same level of linguistic activity. In other words, this is what might appropriately be called horizontal pluralism. (389)
But why should pluralism be restricted to the horizontal? Why should pluralism be associated only with what might be called “discourse monism”? Traditional science has a knack for extracting particularly clear and long-lived patterns and expressing their form in an implementable way (generally through mathematics). What about everything else?
If these [scientific discourses] are cases of horizontal pluralism, what would be a vertical pluralism? It would be the view that philosophy should recognize an irreducible plurality of kinds of discourse—the moral as well as the scientific, for example. This is the species of pluralism with which we ... [should] be most concerned. (Price, 1992, 390)
Price refers to this type of vertical pluralism as discourse pluralism. Here he has arrived at a description of what is meant by pluralism in a complexity-inspired evolutionary philosophy. This type of pluralism is not “irrealist” at all. It simply accepts that in the absence of a completely realist position, one may profit from the examination of a variety of other worldviews and discourses whose sensitivity to noise varies. Different scientific worldviews may be as useful as different moral worldviews or different artistic worldviews (such as cubism or abstract expressionism), all of which are metaphors or caricatures of reality. This does not lead to an “anything goes” relativism, except maybe as a starting point. But how, if one is to make a decision one way or another, is one to untangle the pluralist web and agree upon, albeit temporarily and locally, a dominant worldview? The aim, after all, of analysis is generally to act in an informed way to achieve particular outcomes. Suggesting that one must approach every issue from every angle will quickly lead to paralysis from over-analysis.
The above discussion is included to show that it is not the case that to examine complexity one must use only the tools that have been developed by the complexity community. A complexity-inspired philosophy itself argues that all the tools for thought have the potential to provide insights, albeit provisionally and limitedly, concerning the operation of complex systems. It is not necessary to only use complexity tools as long as one’s thinking is complex. Even linear models used appropriately can be very useful in temporarily understanding complexity. What is more, by maintaining a critical attitude towards these tools and their use, one can resist the possibility of becoming locked into a particular analytical attractor—complex systems evolve and one’s thinking about them needs to evolve as well.
A number of “meta-methodologies” have been proposed that explicitly acknowledge that the recognition of complexity requires an alternative approach to policy analysis. These include total systems intervention (Flood and Jackson, 1991; Flood, 1995), system of systems methodologies (Jackson and Keys, 1984), group modeling (Vennix, 1996), systemic intervention (Midgley, 1997; 2000), and robust adaptive planning (Lempert, 2002b; Bankes, 2002), to name but a few.
A Note on Ethics
A critically pluralist decision making process has to come to an end at some point and a decision made. Literally, the concept of critical (vertical and horizontal) pluralism provides no end—the more one explores, using the mechanisms of critical thinking (critical systems heuristics, critical appreciation, and boundary critique, for example), the richer the understanding and presumably the better-quality the decision. This is, however, impractical.
Analysis is performed to provide insight into a particular problematic situation and has limited time and resources associated with it. Free unimpeded exploration does not and can not be sufficient on its own—one need to recognize that an endpoint must be reached, which in so doing, limits exploration, and therefore limits the breadth and quality of the understanding developed. These shortfalls mean that something important might be missed, and so there are unavoidable risks associated with any decision process. This is where ethics becomes useful, but not as a way to specifically prescribe an endpoint.
By ethics it is not meant purely as some notion of altruism; conversely, in being unable to know it all (the darkness principle), one must accept the inevitability of choices that cannot be backed up scientifically or objectively (Cilliers, 2000a). This means that a judgment must be made that accepts that one has arrived at the best decision possible (given current capabilities), but it is not perfect as a decision can only be based on the insight developed through limited (bounded) effort. One must accept that decisions are based on incomplete analysis, and that potentially adverse outcomes might occur as a result of an inability to see everything. The analysis must be judged to be good by judging how it went about addressing the problem situation and how it critically appraised the determined boundaries. An analysis does not remove the responsibility from the decision maker (one cannot blame the plan if all goes wrong); the decision maker has the responsibility to ensure that the best possible exploration was performed. The decision maker must fully appreciate that the validity of the understanding derived depends wholly on the assumptions (both tacit and explicit) that were made (which may or may not be appropriate given the problematic situation despite considerable effort), and that it is provisional in that it is based upon current beliefs and perceptions. An awareness of both the contingency and provisionality of the analysis is far better than a false sense of security, the latter being a very risky state of affairs indeed. It is clear, though, that there are ethical implications for all boundary judgments.
This approach to ethics does not provide a definitive endpoint for the decision process (this point has to be negotiated between the process participants and reality) but it does provide guidelines as to which factors must be taken into account in determining whether or not an analysis has served its
TABLE 11.1 Useful Complexity and Policy Analysis References
| Title | Reference | Topic |
|---|---|---|
| Complexity and healthcare: a view from the street | Kernick, ed. (2004) | This book explores the application of complexity theory to healthcare with the aid ofboth theory and case-based analyses. Recently reviewed by Baskin (2004). |
| A new mind for policy analysis | Goktug Morçöl (2002) | In this book the author argues for a new view of policy analysis that transcends the prevailing Newtonian approaches. |
| Systemic intervention | Gerald Midgley (2000) | Although this book is not officially a ‘complexity' book, the methodological discussions presented do resonate with those discussed herein and elsewhere in the ‘complexity' literature. |
| Complexity theory and the social sciences | Byrne (1998) | Introduces the central ideas which surround the chaos/ complexity theories. It discusses key concepts and uses them to investigate the nature of social research. |
| Nonlinear dynamics, complexity and public policy | Elliott and Kiel, eds. (1999) | Introduction to the fields of nonlinear dynamics and complex systems, with particular application to a wide range of policy-related issues. |
| Managing complex networks: strategies for the public sector | Kickert, Klijn and Koppenjan, eds. (1997) | Develops a network management approach to governance and public management, and shows how governments can manage policy networks to enhance policy performance and public service delivery. |
| Taking complexity seriously | Roe (1998) | Applies the policy analysis technique of triangulation to sustainable development in complex uncertain systems. |
| Complexity and the economy | Finch and Orillard (2005) | Surveys conceptual approaches to understanding complexity as a key subject in evolutionary and political economy. |
| Managing organizational complexity | Richardson, ed. (2005) | Contains chapters concerning the philosophy, theory and application of complexity science to the understanding of human organisations. |
| Managing complexity in the public services | Haynes (2003) | Argues that the complexity of the public policy process limits the usefulness of the "new public management” approach, and proposes alternative approaches that are based on an understanding of the disorder in the policy process. |
| Full spectrum analysis: practical or in the face of the human variable | Mathieson (2004) | Explores the difficulties in understanding human systems and proposes that "full spectrum analysis,” which is similar to critical pluralism, is needed to rationally intervene in such systems. |
| The complexity of concept mapping for policy analysis | Trochim (2005) | Suggests that the use of concept mapping in combination with other types of human simulation provides a valuable methodological tool for studying complex human systems. |
| From worst slum to best example of regeneration: Complexity in the regeneration of hulme— manchester | Moobela (2005) | A case-based paper illustrating the application of complexity thinking to a regeneration project. |
| Facilitating resource decision making in public organisations drawing upon insights from complexity theory | Kernick (2005) | Explores how complexity insights can be used to facilitate resource decision making in public systems. |
| Robust policy analysis for complex open systems | Bankes (2005) | Describes an approach to highly interactive decision support based upon using ensembles of alternative models, robust option analysis, and adaptive strategies. |
purpose. Essentially, an ethic must be developed locally, rather than falling back on a prescribed universal framework. However, a locally developed ethic may have to be defended non-locally. How might this defense be achieved? This is not a trivial issue, but will not be discussed further here.
Applying Complexity to Policy Analysis
The aims of this chapter are far too ambitious to hope to achieve them in any complete way. The principal aim was to introduce a number of the ideas and developments in complexity theory and to explore in a general way only their implications for policy analysis. However, despite its introductory nature it would be remiss to not include references to actual applications of complexity thinking in policy analysis. Until recently, complexity thinking was regarded more as an academically interesting area of exploration rather than a body of knowledge that could be brought to bear on the solution (albeit non-optimally and provisionally) of real world policy-related problems. This state of affairs is changing rapidly, however, as the field matures. In an attempt to capture only a small part of these developments, Table 11.1 list some key references in the application of complexity thinking to policy analysis. These references should provide useful points of departure for the reader keen to further explore the application of complexity thinking to policy analysis.
Summary and Some Conclusions
Despite its length—which is due to its introductory nature—the main argument of this chapter is straightforward. There are many new tools available to policy analysts that can facilitate the job of comprehending complex systems, and intervening in them in a quasi-rational way. A subset of these tools and concepts was discussed in the first section. However, despite the widespread emergence of new tools, there is also a growing awareness of the limitations of any and all tools for understanding complex systems. Indeed, there is no way to fully comprehend a complex system and therefore no way to intervene in them in a totally risk-free way—taking action always means taking a step into the unknown, to some degree. An understanding of complexity requires an understanding of the limits to one’s analyses. Such an understanding changes the way in which we regard these tools— not as accurate representations of reality, but as useful fictions to facilitate limited sense making. So complexity thinking is not only about the tools used, but also how those tools are used.
A complexity-inspired analytical philosophy does not privilege the accepted tools of complexity researchers as the only legitimate tools for understanding complexity, but argues that all tools have the potential to shed some light on the behavior of such systems. It is the maintenance of a critical stance that becomes essential so that analysts do not get locked into one particular analytical attractor. This shift from analytical lock-in, a pre-occupation with models and not the process of modeling, and an explicit recognition of limits is quite different from many traditional analysis departments. Complexity thinking not only has implications for how the analysis department operates, but also how that department interacts with the rest of an organization, and how that organization as a whole makes decisions if the position of critical pluralism is to be truly acknowledged. Such cultural considerations are difficult to implement given how resistant cultural lock-in is, but to effectively consider the analysis and intervention in complex systems, these cultural concerns are as important as, if not more important than, the analytical tools themselves.
Footnotes
References
Adamic, L. A. The small world web. In Proceedings of the Third European Conference, ECDL’99. Springer-Verlag, Berlin, 443–452.
Albert, R. and Barabási, A.-L., Statistical mechanics of complex networks, Reviews of Modern Physics, 74(1), 47–97, 2002.
Allen, P. M., Evolutionary complex systems: models of technology change, In Evolutionary Economics and Chaos Theory: New Directions in Technology Studies, Leydesdorff, L. and van den Besselaar, P., Eds., St. Martin’s Press, New York, pp. 1–17, 1994.
Allen, P. M., Boulton, J. G., Strathern, M., and Baldwin, J., The implications of complexity for business process and strategy, In Managing the Complex: Philosophy, Theory and Applications, Richardson, K., Ed., Information Age Publishing, Greenwich, CT, pp. 397–418, 2005.
Alligood, K. T., Sauer, T. D., and Yorke, J. A., Chaos: An Introduction to Dynamical Systems, Springer-Verlag, New York, 1997.
Auyang, S. Y., Foundations of Complex-System Theories in Economics, Evolutionary Biology, and Statistical Physics, Cambridge University Press, New York, 1999.
Badii, R. and Politi, A., Complexity: Hierarchical Structures and Scaling in Physics Cambridge Nonlinear Science Series, 6, Cambridge University Press, New York, 1997.
Bak, P., How Nature Works: The Science of Self-organized Criticality, Copernicus, New York, 1996.
Bankes, S., Robust policy analysis for complex open systems, Emergence: Complexity and Organization, 7(1), 2005.
Bankes, S. C., Tools and techniques for developing policies for complex and uncertain systems, Proceedings of the National Academy of Sciences, 99(suppl. no.3), 7263–7266, 2002.
Barabási, A.-L., Linked: The New Science of Networks, Perseus Publishing, Cambridge, MA, 2002.
Barabási, A.-L. and Albert, R., Emergence of scaling in random networks, Science, 286, 509–512, 1999.
Bilke, S. and Sjunnesson, F., Stability of the Kauffman model, Physical Review. E, 65, 0161295, 2001.
Bonabeau, E., Agent-based modeling: methods and techniques for simulating human systems, Proceedings of the National Academy of Sciences, 99(suppl. no. 3), 7280–7287, 2002.
Boosomaier, T. R. J. and Green, D., Complex Systems, Cambridge University Press, Cambridge, UK, 2000.
Byrne, D., Complexity Theory and the Social Sciences: An Introduction, Routledge, London, 1998.
Chaitin, G. J., The Limits of Mathematics, Springer, Singapore, 1999a.
Chaitin, G. J., The Unknowable, Springer, Singapore, 1999b.
Cilliers, P., Complexity and Postmodernism: Understanding Complex Systems, Routledge, London, 1998.
Cilliers, P., What can we learn from a theory of complexity?, Emergence, 2(1), 23–33, 2000a.
Cilliers, P., Knowledge, complexity, and understanding, Emergence, 2(4), 7–13, 2000b.
Cilliers, P., Boundaries, hierarchies and networks in complex systems, International Journal of Innovation Management, 5(2), 135–147, 2001.
Cross, R. and Parker, A., The Hidden Power of Social Networks: Understanding How Work Really Gets Done in Organizations, Harvard Business School Press, Boston, 2004.
Davies, B., Exploring Chaos: Theory and Experiment, Perseus Books, New York, NY, 1999.
Dennett, D. C., Real patterns, The Journal of Philosophy, 88, 27–51, 1991.
Elliott, E. W. and Kiel, L. D., Eds., Nonlinear Dynamics, Complexity and Public Policy, Nova Science Publishers, 1999.
Emmeche, C., Köppe, S., and Stjernfelt, F., Levels, emergence, and three versions of downward causation, In Down Ward Causation, Andersen, P. B., Emmeche, C., Finnemann, N. O., and Christiansen, P. V., Eds., Aarhus University Press, Aarhus, Netherlands, pp. 13–34, 2000.
Erdős, P. and Rényi, A., On random graphs, Publ. Mathematical, 6, 290–297, 1959.
Finch, J. and Orillard, M., Complexity and the economy: Implications for Economic Policy, Edward Elgar Publishing, Cheltenham, UK, 2005.
Flood, R. L., Total systems intervention (TSI): a reconstitution, Journal of the Operational Research Society, 46, 174–191, 1995.
Flood, R. L. and Jackson, M. C., Creative Problem Solving: Total Systems Intervention, John Wiley & Sons, Chichester, UK, 1991.
Haynes, P., Managing Complexity in the Public Services, Open University Press, Milton Keynes, UK, 2003.
Horgan, J., From complexity to perplexity, Science, 272, 74–79, 1995.
Jackson, M. C. and Keys, P., Towards a system of systems methodologies, J. Opl. Res. Soc., 33, 473–486, 1984.
Kauffman, S. A., The Origins of Order: Self-Organization and Selection in Evolution, Oxford University Press, Oxford, UK, 1993.
Kernick, D., Facilitating resource decision making in public organizations drawing upon insights from complexity theory, Emergence: Complexity and Organization, 7(1), 2005.
Kernick, D., Ed., Complexity and Healthcare: A View from the Street, Radcliffe Medical Press, Abingdon, UK, 2004.
Kickert, W. J. M., Klijn, E-H. , and Koopenjan, J. F. M., Eds., Managing Complex Networks: Strategies for the Public Sector, Sage, London, UK, 1997.
Lempert, R. J., Agent-based modeling as organizational and public policy simulators, Proceedings of the National Academy of Sciences, 99(suppl. no. 3), 7195–7196, 2002a.
Lempert, R. J., A new decision sciences for complex systems, Proceedings of the National Academy of Sciences, 99(suppl. no. 3), 7309–7313, 2002b.
Lissack, M. R., Mind your metaphors: Lessons from complexity science, Long Range Planning, April, 294–298, 1997.
Lissack, M. R., Complexity: the science, its vocabulary, and its relation to organizations, Emergence, 1(1), 110–126, 1999.
Lorenz, E. N., Deterministic nonperiodic flow, Journal of the Atmospheric Sciences, 20, 130–141, 1963.
Lucas, C. Complexity and Artificial Life: What are they?, http://www.calresco.org/cal.htm/ (August 3, 2005), 2004.
Lui, H. and Richardson, K. A., Chaos-based principles for forecasting, In Managing Organizational Complexity: Philosophy, Theory, Application, Richardson, K. A., Ed., Information Age Publishing, Greenwich, CT, pp. 167–182, 2005.
Masani, P. R., Three modern enemies of science: materialism, existentialism, constructivism, Kybernetes, 30, 278–294, 2001.
Mathieson, G. M., Full spectrum analysis: practical OR in the face of the human variable, Emergence: Complexity and Organization, 6(4), 51–57, 2004.
May, R. M., Simple mathematical models with very complicated dynamics, Nature, 261, 459, 1976.
McKelvey, W., What is complexity science? It is really order-creation science?, Emergence, 3(1), 137–157, 2001.
McMillan, E., Encouraging strategic change by using complexity-based principles: A case study of the Open University, U.K., In Managing Organizational Complexity: Philosophy, Theory, Application, Richardson, K. A., Ed., Information Age Publishing, Greenwich, CT, pp. 505–520, 2005.
Midgley, G., Mixing methods: Developing systemic intervention, In Multi-Methodology: The Theory and Practice of Combining Management Science Methodologies, Mingers, J. and Gill, A., Eds., John Wiley & Sons, Chichester, UK, 1997.
Midgley, G., Systemic Intervention: Philosophy, Methodology, and Practice, Kluwer Academic, New York, NY, 2000.
Moobela, C., From worst slum to best example of regeneration: Complexity in the regeneration of Hulme-Manchester, Emergence: Complexity and Organization, 7(1), 2005.
Morçöl, G., A New Mind for Policy Analysis: Toward a Post-Newtonian and Postpositivist Epistemology and Methodology, Praeger, Westport, CT, 2002.
Morgan, G., Images of Organization, Sage, Newbury Park, CA, 1986.
Oreskes, N., Shrader-Frechette, K., and Belitz, K., Verification, validation, and confirmation of numerical models in the earth sciences, Science, 263, 641–646, 1994.
Ott, E., Chaos in Dynamical Systems, 2nd ed., Cambridge University Press, Cambridge, UK, 2002.
Powell, J. H., An application of a network-based futures method to strategic business planning, Journal of the Operational Research Society, 48, 857–872, 1997.
Powell, J. H. and Coyle, R. G., A network-based futures method for strategic business planning, Journal of the Operational Research Society, 48, 793–803, 1997.
Price, H., Metaphysical pluralism, The Journal of Philosophy, 89, 387–409, 1992.
Richardson, K. A., On the limits of bottom-up computer simulation: towards a nonlinear modeling culture. Proceedings of the 36th Hawaiian International Conference on System Sciences, California: IEEE, 2003.
Richardson, K. A., On the relativity of recognising the products of emergence and the nature of physical hierarchy. Proceedings of the 2nd Biennial International Seminar on the Philosophical, Epistemological and Methodological Implications of Complexity Theory, January 7th–10th, Havana International Conference Center, Cuba, 2004a.
Richardson, K. A., The problematization of existence: towards a philosophy of existence, Nonlinear Dynamics, Psychology, and Life Sciences, 8(1), 17–40, 2004b.
Richardson, K. A., Systems theory and complexity: part 2, Emergence: Complexity and Organization, 6(4), 77–82, 2004c.
Richardson, K. A., The hegemony of the physical sciences: an exploration in complexity thinking, Futures, 37, 615–653, 2005a.
Richardson, K. A., Complexity thinking and policy analysis, 2005b.
Richardson, K. A., The role of “waste” in complex systems. Paper presented at the 1st International Workshop on Complexity and Policy Analysis, Cork, Ireland, 2005c.
Richardson, K. A., Ed., Managing Organizational Complexity: Philosophy, Theory, Application, Information Age Publishing, Greenwich, CT, 2005.
Richardson, K. A. and Cilliers, P., “What is complexity science? A view from different directions., Emergence, 3(1), 5–23, 2001.
Roe, E., Taking Complexity Seriously: Policy Analysis, Triangulation and Sustainable Development, Kluwer Academic, New York, 1998.
Simon 1945, H., Administrative Behavior: A Study of Decision-Making Processes in Administrative Organizations, 4th ed., The Free Press, New York, 1945.
Skyttner, L., General Systems Theory: Ideas and Applications, World Scientific, Singapore, 2001.
Sommerer, J. C. and Ott, E., A physical system with qualitatively uncertain dynamics, Nature, 365, 138–140, 1993.
Trochim, W., The complexity of concept mapping for policy analysis, Emergence: Complexity and Organization, 7(1), 2005.
Van Eijnatten, F. and van Galen, M., Provoking chaordic change in a dutch manufacturing firm, In Managing Organizational Complexity: Philosophy, Theory, Application, Richardson, K. A., Ed., Greenwich, CT, Information Age Publishing, pp. 521–556, 2005.
Vennix, J. A. M., Group Model Building: Facilitating Team Learning Using System Dynamics, John Wiley & Sons, Chichester, UK, 1996.
Watts, D. J. and Strogatz, S. H., Collective dynamics of “small-world networks”, Nature, 393, 440–442, 1998.
Wolf, A., Quantifying chaos with Lyapunov exponents, In Chaos, Holden, A. V., Ed., Princeton University Press, Princeton, NJ, pp. 273–290, 1986.
Yook, S., Jeong, H., and Barabási, A.-L. Modeling the Internet’s large-scale topology, 2001.http://arxiv.org/abs/cond-mat/0107417/