On the Limits of Bottom-Up Computer Simulation: Towards a Nonlinear Modeling Culture1
Kurt A Richardson
Abstract: In the complexity and simulation communities there is growing support for the use of bottom-up computer-based simulation in the analysis of complex systems. The presumption is that because these models are more complex than their linear predecessors they must be more suited to the modeling of systems that appear, superficially at least, to be (compositionally and dynamically) complex. Indeed the apparent ability of such models to allow the emergence of collective phenomena from quite simple underlying rules is very compelling. But does this ‘evidence’ alone ‘prove’ that nonlinear bottom-up models are superior to simpler linear models when considering complex systems behavior? Philosophical explorations concerning the efficacy of models, whether they be formal scientific models or our personal worldviews, has been a popular pastime for many philosophers, particularly philosophers of science. This paper offers yet another critique of modeling that uses the results and observations of nonlinear mathematics and bottom-up simulation themselves to develop a modeling paradigm that is significantly broader than the traditional model-focused paradigm. In this broader view of modeling we are encouraged to concern ourselves more with the modeling process rather than the (computer) model itself and embrace a nonlinear modeling culture. This emerging view of modeling also counteracts the growing preoccupation with nonlinear models over linear models.
Introduction
As with any revolution in thought the products of the ‘new way’ are all too often oversold as tools that will forever fix the apparent gaps in previous methods. Bottom-up computer simulation is no different in this respect. Perhaps as a result of the success of the Santa Fe Institute2, complexity science is often completely associated with mathematical computer-based modeling. Agent-based modeling is seen as a route that the social sciences might finally take in their apparent desire to be a real (hard) science3. Any approach to understanding the world around us has significant limitations, and though bottom-up computer simulation is undoubtedly an incredibly useful sense-making tool, it is no different in this respect.
Why is this concern with the efficacy of our models even important? In recent years there has been a dramatic increase in the use of complex simulations as a means to evaluate social processes. In some instances the predictions generated by these models are being used to inform high-level policy decisions regarding many aspects of modern society. “The developers and users of these models, the decision makers using information derived from the results of the models, and people affected by decisions based on such models are rightly concerned [or they should be] with whether a model and its results are ‘correct’” [2].
Emerging Schools of Complexity Thought
Richardson & Cilliers [3] have identified three broad schools of complexity science, namely new reductionism, soft complexity and complexity thinking. In the field of computer-based simulation new reductionism understand-ably drowns out the other complexity schools of thought with its focus on computer models and the search for absolute theories of complexity. This version of complexity dominates much of the literature beyond simulation sciences and is the focus of most conferences that aim to explore complexity ‘science’. It is perhaps interesting to note that many supposed complexity scientists, who often go out of their way to ridicule the naïve and simplistic mechanistic paradigm, often retain most of the same underlying assumptions4 that they claim not to – hence the term New Reductionists.
Soft complexity thinking refers to the preoccupation, particularly in the North American management science community, with the use of metaphor (without criticism)5. This school argues that complexity justifies (atheoretical) pluralism and the uncritical use of metaphor in the understanding of social organizations. This also draws upon the belief in widespread homologies (e.g. the frequent appearance of the standard wave-equation in apparently disconnected fields of study) that motivated the searchers of a general theory of systems. Soft complexity is essentially a radically relativist philosophy.
Complexity thinking, which will be the general lens for this paper, takes for granted the ontological assumptions of complexity (i.e., that the universe is constructed from non-linearly interacting fundamental components) and explores the epistemological consequences, i.e. the insights that can be drawn from complexity regarding our process of sense making (or, the process of model building). The main conclusion is that a form of critical pluralism meets the epistemological requirements determined from the complexity ontology, i.e. the need for critical approaches and the use of a wide variety of different perspectives (qualitative or quantitative) naturally follows from the underlying assumptions of complexity.
Aims of Paper
The aim of this paper is to critique nonlinear bottom-up computer simulation in terms of the emerging complexity thinking philosophy which in turn is partially developed from the field of nonlinear bottom-up computer simulation. In doing so I will consider: the concept of equifinality and its consequences for multiple non-overlapping explanations of the same phenomena (and therefore the validation process, and the potential for knowledge transfer); the status of knowledge derived from the modeling of complex systems; strong exploration versus weak exploration; linear versus nonlinear modeling ‘culture’, as well as the role that simulation plays in the organization decision process. The result is a complexity informed modeling paradigm that is considerably broader than the computer-based paradigm.
In a paper published in JASSS Chris Goldspink discussed the methodological implications of complex systems approaches to the modeling of social systems [5]. Like others before him Goldspink advocated the use of bottom-up computer simulations for examining social phenomena. It is argued therein that computer simulation offers a partial solution to the methodological crisis apparently observed in the social sciences. Though I agree with many of Goldspink’s remarks I personally feel that BUCS has been oversold as a tool for modeling and managing organizational complexity at the expense of other equally legitimate (from a complex systems stance) approaches. I have no doubt that BUCS offer a new and exciting lens on organizational complexity, but we must explicitly recognize that this nonlinear approach suffers from some of the same limitations as its linear predecessors. The aim of this paper, therefore, is to discuss some of the limitations in more detail and suggest that complexity thinking offers a simulation paradigm that is broader than the new reductionism of BUCS. This alternative interpretation of complexity thinking forces us to reconsider the relationship between our models and ‘reality’ as well as the role simulation plays in decision making processes.
Many of the conclusions drawn herein will be familiar to those who pay attention to the philosophical debates surrounding the efficacy of our models. What I personally find of interest is that these conclusions can be derived from the field of bottom-up computer simulation itself. In a sense the bottom-up perspective contains within itself evidence of a broader perspective.
On the Limits of Bottom-Up Computer Simulation
A Seductive Syllogism
In the above typology new reductionism is associated with the representationalist view that real life complex systems can best be modeled through the exploration of bottom-up computer simulations (BUCS); an approach often associated with the Santa Fe Institute. This school of complexity science is based on a seductive syllogism [6]:
Premise 1: There are simple sets of mathematical rules that when followed by a computer give rise to extremely complicated patterns.
Premise 2: The world also contains many extremely complicated patterns.
Conclusion: Simple rules underlie many extremely complicated phenomena in the world, and with the help of powerful computers, scientists can root those rules out.
So simply because BUCS representations appear to be compositionally similar to the real world (when viewed through a complex systems lens) then they must be better representations than others. Though this syllogism was refuted in a paper by Oreskes et al. [7], in which it the authors warned that “verification and validation of numerical models of natural systems is impossible,” this position still dominates what has become to be known as complexity studies6. Despite its refutation this same syllogism seems to be the basis of Wolfram’s [8] attempt to formulate A New Kind of Science.
The term new reductionism is associated with BUCS because, despite the attempt to explicitly build-in the apparent real world complexity to the computer models, these models are still gross simplifications of reality7. Furthermore, many users of BUCS regard their models in a modernist, or realist, manner which assumes to some extent that ‘what we see is what there is’ thereby trivializing the recognition of constituent object boundaries [9], as well as giving a false sense of realism/objectivity regarding these models. Modernist (or linear) interpretations also focus on the model itself (the computer representation) rather than on the modeling process8.
The key idea that is used initially herein to critique BUCS is the concept of equifinality, i.e. the existence of multiple non-overlapping explanations for the same phenomenon.
Equifinality and Multiple Explanations
The concept of equifinality is defined as “the tendency towards a characteristic final state from different initial states and in different ways” [10]. We can state this ‘law’ in different ways9:
- There are many paths/trajectories to the same state (see figure 1).
- There are potentially many non-overlapping qualitatively different explanations/models for any particular phenomena resulting from nonlinear interactions
- An infinitude of micro-architectures will give the same subset of macro-phenomena that correspond to our observations.
This places some very severe limitations to usefulness of nonlinear computer simulations. Firstly, given the intractability of the emergent phenomena that occur within the simulation the analyst might not be able to provide any insights into the chain of events that led to a particular (modeled) system state. So, there is the possibility that the simulation itself might not offer any explanatory capability whatsoever even if the final state does indeed resemble ‘real’ systems’ behavior(s). Potentially worse still is that assuming that the Universe can best be considered a complex system, there are an enormous number of qualitatively different ways to model the same phenomena. As Maxwell [11] in his new conception of science says:
“Any scientific theory, however well it has been verified empirically, will always have infinitely many rival theories that fit the available evidence just as well but that make different predictions, in an arbitrary way, for yet unobserved phenomena.”
This means that any theory/model, whether it be a non-linear bottom up view or not, will be limited in its use because of underdetermination, i.e. given any amount of evidence, there are mutually incompatible models which equally fit with the evidence ("...the evidence cannot by itself determine that some one of the host of competing theories is the correct one" [12]), and that when a prediction from a model contradicts the observation, there are various mutually incompatible ways for making the model compatible with the evidence (parameter tuning for example).
A result of equifinality is that even if our models can be used to develop causal explanations10 (within the confines of the model) we cannot be sure that those explanations bear any relationship to reality whatsoever11. As Lansing [14] reminds us:
“One does not need to be a modeler to know that it is possible to ‘grow’ nearly anything in silico without necessarily learning anything about the real world.”
And,
“…computers offer a solution to the problem of incorporating heterogeneous actors and environments, and nonlinear relationships (or effects). Still, the worry is that the entire family of such solutions may be trivial, since an infinite number of such models could be constructed.”
Also, quoted in Lansing [14], John Maynard Smith writes that he has:
“…a general feeling of unease when contemplating complex systems dynamics. Its devotees are practicing fact-free science. A fact for them is, at best, the outcome of a computer simulation; it is rarely a fact about the world.”
These are the potentially crippling effects that result from nonlinearity.
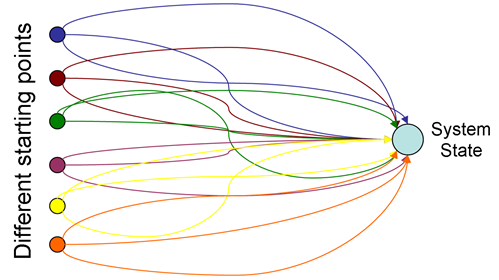
Figure 1 Illustration showing that not only can a particular system state (outcome) can be reached via different trajectories from the same starting conditions, but also that different starting conditions may also lead to the same system state (indicating the existence of an attractor in phase space). Of course, the reverse case is also a possibility in that different starting conditions may lead to different outcomes (indicating the existence of multiple attractors) and multiple runs from the same starting conditions may also result in different outcomes12.
It is tempting to think that equifinality is only of concern in particularly complex systems – but we would be quite wrong to think this. Equifinality is ubiquitous. Even in incredibly simple 1-dimensional cellular automatons the presence of equifinality is more than clear. Figure 2 illustrates this by showing selected non-equivalent attractor basins for a particular 1-d cellular automaton (the details of which are unimportant for this discussion). At the centre of each image is one of the system’s attractors, i.e. a collection of end-states. The attractor branches depict the many different trajectories that can be taken to reach different attractors. (Refer to [15, 16, 17, 18] for full details.)
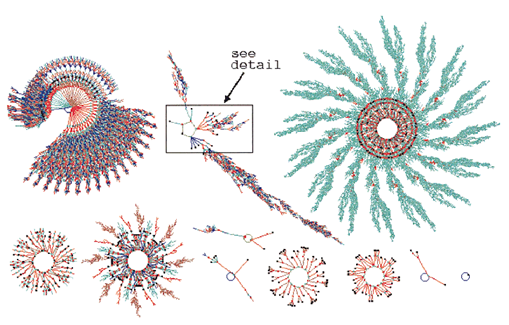
Figure 2 Non-Equivalent Basins of Attraction for a Simple 1-dimensional Cellular Automata of Size, n=16. (Taken from [18]).
The Status of Theories: Linear versus Non-Linear
Figure 3 attempts to illustrate these significant shortcomings by comparing linear systems to nonlinear systems. Figure 3a demonstrates the triviality of linear problems assuming that the universe (or at least the part we might be interested in modeling)13 and our models of it are linear. The thick red line that appears between the two vertical dotted lines traces some real world empirical data. Because the system is linear (or can at least be temporarily and provisionally assumed to the linear) we can be sure that, though we only have data for some subset of all possible contexts, the system will continue to behave linearly in (qualitatively similar) contexts for which we have no data. The thinner colored lines represent outputs from some of the linear models that might be developed to explain the observed data. Though there is an infinity of possible qualitatively similar models that nearly fit the data (all being of the form y = mx + c) none of them deviate much from the observed data. And, though these models have been validated against a limited set of contexts we can be confident that the models still hold for qualitatively similar contexts for which we have no data. Furthermore, we only need to validate our models against limited data to ensure that they are valid for all qualitatively similar contexts14. (All other contexts will of course be qualitatively similar as there are no emergent processes). So, the knowledge contained in our models can be easily transferred to other contexts – assuming that the world and our models are linear.
Figure 3b shows a very different picture. Like before the thick red line depicts actually observed data for a limited range of contexts (delimited by the two vertical dotted lines). Unlike before, the data relates to a particular phenomenon that arises nonlinearly rather than linearly – a complex Universe. Now, the thinner colored lines represent outputs from a selection of qualitatively different nonlinear models (such as BUCS) that have been ‘tuned’ (or ‘fudged’) to account for the observed data. As can be seen, the predictions made by these nonlinear models for contexts of which we have no observations may vary wildly. Of course, we could expand our data set by collecting data for an expanded set of contexts, but we would still be left with the same problem. In fact, the only scenario in which one model could be chosen over all others is by validating each model against data collected for all possible contexts. This is absurdly impractical and yet is the case even if the real world system is qualitatively stable. As is well known, real world systems are not necessarily qualitatively stable as new entities can emerge (i.e. its ontology is dynamic), and order parameters that describe the key features of a real world (complex) system one day may be qualitatively inaccurate the next15. This would seem to indicate that absolute knowledge concerning a nonlinear universe is impossible. Furthermore, there is no proof that any practical knowledge we might acquire would be at all transferable. Fortunately, these limitations represent an extreme situation – since when have we needed absolute (certain) knowledge for most purposes? However, it is clear that the relationship between our models and therefore our knowledge of real world systems is not a trivial one-to-one mapping as once assumed – the actual relationship is very complex indeed.
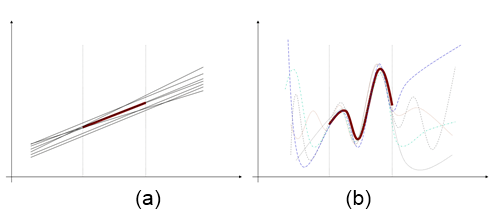
Figure 3 Linear Models of a Linear Universe versus Nonlinear Models of a Nonlinear Universe. (For linear systems extrapolation from limited data is a trivial exercise, whereas for nonlinear systems extrapolation from limited data is a highly problematic exercise.)
These limitations concerning the validation of models16 of real world complex systems exist for both linear and nonlinear approaches, i.e. these limitations are not overcome through the implementation of BUCS.
Towards a Nonlinear Modeling Culture
Strong versus weak exploration
Though bottom-up computer simulations are susceptible to the some of the same limitations as linear approaches BUCS do allow the exploration of the idealized systems state space which partially mitigates against the limitations discussed above.
Elsewhere Richardson et al. [21] identify two types of exploration: weak and strong exploration where weak refers to intra-perspective (or quantitative) exploration and strong refers to inter-perspective (qualitative) exploration. It is argued therein that both strong and weak explorations are essential in the investigation of complex systems like socio-technical systems. Weak exploration encourages the critical examination of a particular perspective, which is undoubtedly driven by its differences with other perspectives. Strong exploration encourages the sucking in of all available perspectives in the considered development of a situation-specific perspective not plagued by dogmatic views. These two types of exploration are not orthogonal, and cannot operate in isolation from each other. The greater the number of perspectives available, the more in depth the scrutiny of each individual perspective will be; the deeper the scrutiny the higher the possibilities are of recognizing the value, or not, of other perspectives. Essentially complexity-based analysis, Richardson et al. argued, is a move from the contemporary authoritarian (or imperialist [22]) style, in which a dominant perspective bounds the analysis, to a more democratic style that acknowledges the ‘rights’ and potential value of a range of perspectives which needn’t be mathematically based and are certainly not restricted to computer-based simulations. The decision as to what perspective to use is deferred until after a process of contextual and paradigmatic exploration.
Most of the BUCS-type analysis that I have been involved in focuses mainly on weak exploration (albeit in a form much stronger than traditional linear approaches), i.e. the exploration of the idealized system’s state space via the quantitative variation (rather than qualitative variation) of the model’s underlying assumptions. Essentially this is sensitivity analysis. Such analysis does facilitate the exploration of hypotheses and the checking of robustness of models by an exhaustive search of parameter space [5]. However, throughout such an analysis the qualitative form of the model is more or less static which limits exploration quite significantly – BUCS may well be useful in uncovering qualitatively different behavioral regimes but they are often based upon a qualitatively static assumption set. With the growing availability though of modeling environments that facilitate bottom-up model construction a number of qualitatively different (though still mathematically based) models can be easily constructed and rigorously analyzed. So it is becoming increasingly straight-forward to perform both strong and weak forms of exploration in BUCS environments albeit in a limited way.
However, despite the increased flexibility of the BUCS approach the focus is still on the model itself rather than the modeling process. Furthermore the strong qualitative exploration is still restricted by a preoccupation with mathematical representations which is not necessarily wholly supported by the complex systems view [4].
Linear versus nonlinear modeling culture
In running to advocate the complexity perspectives many complexiologists have suggested a move away from linear models in favor of nonlinear models. I find this attitude rather baffling considering the successes in mathematics where local problems to nonlinear systems can be found through the process of linearization – maybe it is just fashionable to reject linearity in all its guises. Linearization (illustrated in Figure 4) shows that linear thinking can indeed provide valuable insights, however limited, concerning the behavior of nonlinear systems. In a way, linear thinking is a special kind of nonlinear thinking so we shouldn’t be so hasty in rejecting linear methods. In light of nonlinearity we certainly need to reframe our attitude towards linear approaches, but this most certainly does not support the rejection of such methods.
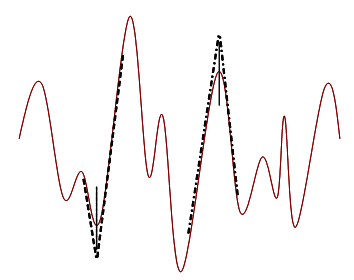
Figure 4 Linearization of a Nonlinear Phenomenon for Restricted Contexts
As argued in the previous section, nonlinear models suffer from many of the shortcomings that linear models do. This section aims to move the focus away from the model itself and onto the modeling process.
Allen [23] has suggested that there are two fundamental assumptions that when taken in different combinations, lead to different modeling approaches. The assumptions expressed simply are: (1) no macroscopic adaptation allowed, and (2) no microscopic adaptation allowed. If both assumptions are made, plus an additional one which assumes that the system will quickly achieve an equilibrium state, then we have an equilibrium-type model – a modeling approach that still dominates much of contemporary economics. If both assumptions are made then we have a basic system dynamics model. If assumption (1) is relaxed then the resultant model will have the capacity to self-organization. And, if both assumptions are relaxed then a truly evolutionary model can be constructed – of which the BUCS approach is a limited example. Figure 5 illustrates the difference between these different modeling approaches in terms of their respective phase portraits.
The reason that I bring up Allen’s conception of complexity modeling is that it leaves no room for linear models. This exclusion seems to support the calls for a complete overhaul of modeling and the disposal of traditional linear tools and methods. To model complex systems well Allen suggests that we should relax both assumptions. In [21] it was suggested that at times a linear model of a complex system may be perfectly adequate (refer back to Figure 4). Why do these two viewpoints disagree? What should be noted is that Allen’s fundamental assumptions deal only with the mathematically conceived model that takes shape on a computer. They do not directly deal with the modeling process itself (which includes the interpretation of the model). If the scope of these assumptions were generalized to refer to the modeling process itself and not just the formally developed model then the place for linear modeling (not linear thinking) is retrieved. As an example, consider a decision tree (Figure 6).
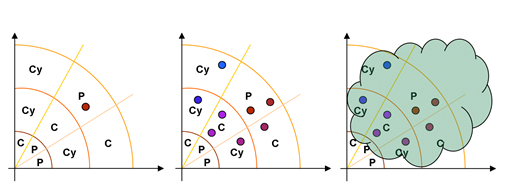
Figure 5 Phase Portraits of Different Modeling Approaches: (a) System dynamics model – the phase space is divided into attractor basins (P – point attractor, Cy – cyclic attractor, C – chaotic attractor), but any trajectory will, after an arbitrary length of time, fall into one of the basins and stay there forevermore; (b) Self-organizing model – the phase portrait is very similar to that of a system dynamics model but trajectories are able to leap between basins (as a result of external perturbations, like noise); (c) Evolutionary model – not only are the trajectories able to jump between different attractor basins, but also the structure of phase space evolves over time. (NB the phase space of an equilibrium model is not represented as such model quickly converges to a system-characteristic point attractor).
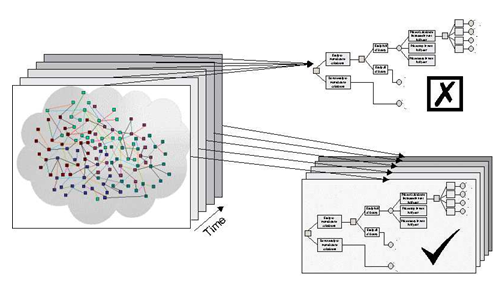
Figure 6 The ‘Evolution’ of a Linear ‘Decision Tree’ Model
A decision tree is a widely used linear decision-making technique. If one were to build such a tree and populate it with the relevant data (generally based upon expert judgments) then it would spew out a set of numbers that can be used to rank different courses of action. Left to its own devices the tree would not evolve in any way (unless the computer failed, or the piece of paper on which it was drawn burnt - in which case the tree would simply disappear!). The model itself has no intrinsic capability to self-organize or evolve in any way. It is a simple linear model. It would be the same next year as it is today and offer exactly the same output given the same input. According to Allen’s typology (when restricted to the model itself) it is worthless as far as complexity modeling is concerned. However, if the tree is used within a modeling environment that does allow for micro and macroscopic adaptation then the tree may also evolve. The modelers can explore possible scenarios by populating the model with different data sets; they can play with the structure of the tree (effecting a re-organization); and even dispose of the tree and decide to use an alternative method (effecting a true evolution – the tree model ‘evolves into’ a cellular automata model possibly, or a simple decision matrix). The ‘culture’ in which the model is used effectively allows for both micro and macroscopic adaptation of the model17. It is for the modelers/decision-makers to judge whether the linear model is appropriate given the currently observed behavior of the real complex system of interest. In making such a judgment they will necessarily continually question the boundaries of the analysis, and explore the potential of a variety of perspectives. The thinking supporting the model development will be nonlinear, despite the potential linearity of the computer model constructed. Of course, the nonlinear modeling process may equally lead to a nonlinear representation, such as a BUCS. The point is that a nonlinear modeling culture neither excludes linear nor nonlinear models.
In short it is argued that accepting Allen’s fundamental assumptions as assumptions regarding the modeling process itself rather than the consequent mathematical representation is a more useful application, which is truer to the analytical requirements inferred from complexity thinking.
The distinction between a linear and nonlinear modeling ‘culture’ is crucial as it highlights the different ways in which the models themselves are regarded. The linear ‘culture’ takes a representationalist view of models in which aspects of reality really are considered to be captured by the model itself – the model becomes an accurate map of reality á la realism. Even if the model itself is nonlinear its efficacy tends to be overstated. As a brief example (based on the author’s personal experience as a government consultant) consider system dynamics ‘flight simulators’. ‘Flight simulators’ are very effective tools for testing out different organizational strategies, tactics and assumptions by facilitating (weak) exploration of the idealized systems state space. In this case, however, rather than use the simulator to develop a ‘feel’ for the behavior of the system of interest, the linear decision makers (regarding the model as an accurate representation, or map, of their organization) simply set the simulator’s ‘dials’ to achieve a particular outcome and then went away to force the ‘dials’ of the real system into the same positions. This demonstrated a gross misunderstanding of how exploratory models should be used to support organizational decision making.
The nonlinear ‘culture’ takes a much more pragmatic stance which recognizes the model as no more than a rough and ready caricature, or metaphor, of reality. As such the knowledge contained in the model should be regarded with a healthy skepticism, seeing it as a limited source of understanding. The (nonlinear) modeling process is regarded as an ongoing dialectic between stakeholders (modelers, users, customer, decision makers, etc.), the ‘model’, and observed reality rather than a simple mapping exercise.
Goldspink [5] lists a number of analytical philosophies (such as soft systems methodologies and action research) which Richardson et al. [19] regard as nonlinear analytical philosophies. To Goldspink’s list I would definitely add critical systems thinking [24] and systemic intervention [25]. Goldspink suggests that quantitative methods, such as BUCS, “… may … be incorporated within these action frameworks.” As a result of the discussion thus far I would tend to stress the potential for incorporation of the qualitative and quantitative methods a little differently: it is essential that quantitative methods be incorporated into a qualitative (nonlinear) analytical framework (such as those listed above) so that the linear application of nonlinear models is avoided.
Kollman et al. [26] states that “[a]n ideal tool for social science inquiry would combine the flexibility of qualitative theory with the rigor of mathematics. But flexibility comes at the cost of rigor.” This may be the case if we persist in holding on to traditional notions of what rigor is. I would argue that the incorporation of quantitative approaches into one of the available qualitative frameworks mentioned above would achieve the balance of flexibility and rigor that Kollman seeks as long as we recognize also that these frameworks must also be regarded with a healthy skepticism too.
Summary
BUCS undoubtedly offer a new and exciting view onto the world of social systems. However, they still suffer from some of the same unavoidable limitations that linear approaches do. Complexity science has impli-cations not only for the models used themselves but also for the way in which such models are regarded and the role they play in the development of the understanding that informs organizational related decisions. At the end of the day models are tools that can be used an abused - the best models are worthless in linear hands. The position discussed briefly herein and elsewhere [21] alludes to a complexity-inspired modeling paradigm which is significantly broader than the representationalist computer simulation philosophy. With the widespread availability of affordable computing power we have witnessed a modeling revolution. Without an associated cultural revolution decision-makers will continue to make the same mistakes often associated with linear mechanistic philosophies.
As commented upon early in this paper, many of the conclusions discussed herein have been made previously. What is new is that rather than the discussion of the efficacy of our models being primarily a philosophical enterprise we now have the tools to explore some of the same issues in a scientific manner; BUCS can be used to appreciate the limitations of BUCS as well as any modeling approach.
Footnotes
References
[1] Richardson, K. A. (2002). “’Methodological implications of complex systems approaches to sociality’: some further remarks,” Journal of Artificial Societies and Social Simulation, 5(2), jasss.soc.surrey.ac.uk/5/2/6.html
[2] Sargent, R. G. (1999). “Verification and Validation of Computer-Based Models,” Proceedings of the 5th International Conference of the Decision Sciences Conference: Integrating Technology and Human Decisions: Global Bridges into the 21st Century, Vol. 2, Dimitris K. Despotis and Constantin Zopouridis (eds.), July 4-7 1999, Athens, Greece.
[3] Richardson, K. A. and Cilliers, P. (2001). "What is Complexity Science? A View from Different Directions," Special Issue of Emergence – Editorial, Vol. 3 Issue 1: 5-22.
[4] Richardson, K. A. (2002). “The Problematization of Existence: Towards a Philosophy of Complexity,” submitted to Nonlinear Dynamics, Psychology, and Life Sciences.
[5] Goldspink, G. (2002). “Methodological Implications of Complex Systems Approaches to Sociality: Simulation as a Foundation for Knowledge,” Journal of Artificial Societies and Social Simulation, Vol. 5, No. 1, http://jasss.soc.surrey.ac.uk/5/1/3.html
[6] Horgan, J. (1995). “From Complexity to Perplexity,” Science, 272: 74-79.
[7] Oreskes, N., Shrader-Frechette, K. and Belitz, K. (1994). “Verification, validation, and Confirmation of Numerical Models in the Earth Sciences,” Science, 263: 641-646.
[8] Wolfram, S. (2002). A New Kind of Science, Wolfram Media, Inc., Champaign, IL, ISBN 1579550088.
[9] Richardson, K. A. (2001). "On the Status of Natural Boundaries: A Complex Systems Perspective," Proceedings of the Systems in Management - 7th Annual ANZSYS conference November 27-28, 2001: 229-238, ISBN 072980500X.
[10] Von Bertalanffy, L. (1969). General System Theory: Foundations, Development, Applications, George Braziller: NY, Revised Edition, ISBN 0807604534.
[11] Maxwell, N. (2000). “A New Conception of Science,” Physics World, August: 17-18.
[12] Klee, R (1997). Introduction to the Philosophy of Science: Cutting Nature at Its Seams, Oxford University Press, ISBN 0195106113, p. 66.
[13] Kagel, J. H., Battalio, R. C. and Green, L. (1995). Economic Choice Theory: An Experimental Analysis of Animal Behavior, Cambridge University Press, New York: NY, ISBN 0521454883.
[14] Lansing, J. S. (2002) "Artificial Societies and the Social Sciences,” Santa Fe Institute Working Paper 02-03-011.
[15] Wuensche, A. and Lesser, M. J. (1992). The Global Dynamics of Cellular Automata, Santa Fe Institute Studies in the Sciences of Complexity, Addison-Wesley, Reading: MA, ISBN 0201557401.
[16] Wuensche, A. (1998a). “Classifying Cellular Automata Automatically,” Santa Fe Institute Working Paper 98-02-018.
[17] Wuensche, A. (1998b). “Discrete Dynamical Networks and their Attractor Basins,” Complexity International, 6, http://life.csu.edu.au/complex/ci/vol6/wuensche/wuensche.html
[18] Wuensche, A. (1999). “Classifying Cellular Automata Automatically: Finding Gliders, Filtering, and Relating Space-Time Patterns, Attractor Basins, and the Z Parameter,” Complexity, 4(3): 47-66.
[19] Bankes, S. & Gillogly, J. (1994). “Validation of Exploratory Modeling,” Proceedings of the Conference on High Performance Computing, Adrian M. Tentner and Rick L. Stevens (eds.), San Diego, CA: The Society for Computer Simulation, pp. 382-387.
[20] Bankes, S. (1993). “Exploratory Modeling for Policy Analysis,” Operations Research, Vol. 41 No. 3: 435-449.
[21] Richardson, K. A., Mathieson, G. and Cilliers, P. (2000). "The Theory and Practice of Complexity Science - Epistemological Considerations for Military Operational Analysis," SysteMexico, 1: 25-66.
[22] Flood, R. L. (1989). “Six Scenarios for the Future of Systems ‘Problem Solving’,” Systems Practice, 2(1): 75-99.
[23] Allen, P. M. (2001). “Economics and the Science of Evolutionary Complex Systems,” SysteMexico, Special Edition – The Autopoietic Turn: Luhman’s Re-Conceptualization of the Social, pp. 29-71.
[24] Flood, R. L. and Romm, N. R. A. (eds.) (1996). Critical Systems Thinking: Current Research and Practice, Plenum Press: NY, ISBN 0306454513.
[25] Midgley, G. (2000). Systemic Intervention: Philosophy, Methodology, and Practice, Kluwer Academic / Plenum Publishers: NY, ISBN 0306464888.
[26] Kollman, K., Miller, J. H. and Page, S. (1997). “Computational Political Economy,” in Arthur, W. B., Durlauf, S. N. and Lane, D. A. (eds.), The Economy as an Evolving Complex System II, Addison-Wesley: Reading MA, ISBN 0201328232, p. 463.
Acknowledgements
I would like to thank I.S.C.E. and Dr. Michael Lissack for supporting the research leading to this paper and many others. Thanks also go to Caroline Richardson for valuable moral support. I am particularly grateful to three anonymous reviewers for comments that assisted me in improving the arguments contained herein.