The Role of ‘Waste’ in Complex Systems

Kurt A. Richardson

Proceedings of the 11th ANZSYS / Managing the Complex V conference, Christchurch, New Zealand, 5th-7th December, 2005

Abstract

In the field of Boolean networks (which are an example of a simple form of complex system) it has been observed that not all comprising nodes participate in the longer term (asymptotic) dynamics of the system, i.e., they can be removed from the network without affecting the network’s macro-dynamical behavior. Do these ‘irrelevant nodes’, or ‘waste’, play a role, or can they really be disposed of in favor of a more efficient network?

Introduction

The eighty-twenty principle of general systems theory has been used in the past to justify the removal of large chunks of an organization’s resources, principally its workforce. According to this principle, in any large system eighty per cent of the output will be produced by only twenty per cent of the system. Of course, the conclusion that a top manager could actually remove 80% of its resources and still maintain its current performance is based on a very faulty interpretation of the above principle. However, assuming not all resources contribute equally to a system’s performance, can we identify in a rational way which resources are superflouous, or ‘waste’?

Recent studies in Boolean networks, a particularly simple form of complex system, have shown that not all members of the network contribute to the function of the network as a whole.

The function of a particular Boolean network is related to the structure of its phase space, particularly the number of attractors in phase space. For example, if a Boolean network is used to represent a particular genetic regulatory network (as in the work of Kauffman, 1993) then each attractor in phase space is said to represent a particular cell type that is coded into that particular genetic network. It has been noticed that the key to the stability of these networks is the emergence of stable nodes, i.e., nodes whose state quickly freezes. These nodes, as well as others called ‘leaf nodes’ (nodes that do not input into any other nodes), contribute nothing to the asymptotic behavior of these networks. What this means is that only a proportion of a dynamical network’s nodes contribute to the long-term behavior of the network. We can actually remove these stable/frozen nodes (and leaf nodes) from the description of the network without changing the number and period of attractors in phase space, i.e., the network’s function. Figure 1 illustrates this. The network in Figure 1b is the reduced version of the network depicted in Figure 1a. I won’t go into technical detail here about the construction of Boolean networks, the interested reader is encouraged to refer to Richardson (2005) for further details. Suffice to say, by the way I have defined network functionality, the two networks shown in Figure 1 are functionally equivalent. It seems that not all nodes are relevant – we might say that a certain percentage of nodes are superfluous to the achievement of the networks particular function and are therefore appropriately considered as ‘waste’. But how many nodes represent ‘waste’?

Figure 1

Figure 1 An example of (a) a Boolean network, and (b) its reduced form. The nodes which are made up of two discs feedback onto themselves. The connectivity and transition function lists at the side of each network representation are included for those readers familiar with Boolean networks. The graphics below each network representation show the attractor basins for each network. The phase space of both networks contain two period-4 attractors, although it is clear that the basin sizes (i.e., the number of states they each contain) are quite different.

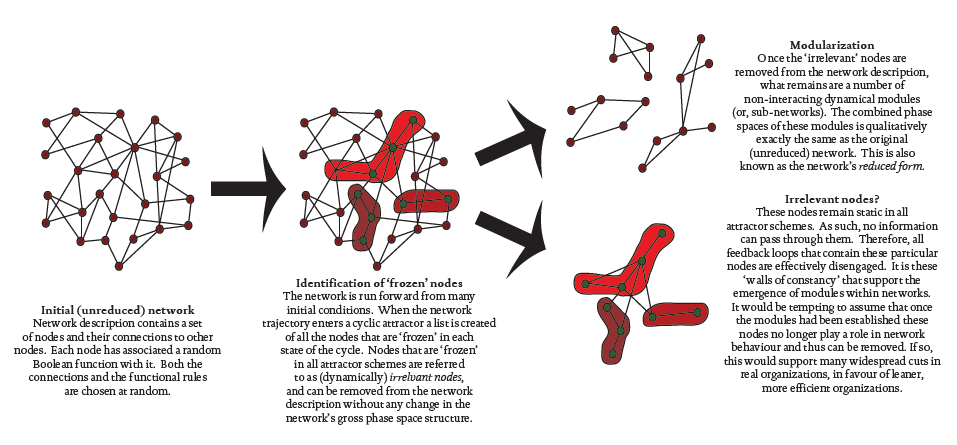
Figure 2

Figure 2 The process of modularization in complex networks

The modularization of complex networks

Before considering the amount of ‘waste’ in a complex network and its role in network behavior we must consider the process of ‘modularization’ in complex networks. Figure 2 illustrates how the emergence of ‘walls of constancy’ divide complex networks up into non-interacting modules. This process, which we might label as an example of horizontal emergence (Sulis, 2005), was first reported by Bastolla and Parisi (1998). It was argued that the spontaneous emergence of dynamically disconnected modules is key to understanding the complex (as opposed to ordered and quasi-chaotic) behavior of complex networks. Through this process we begin to understand a important role for the supposed ‘waste’.

Understanding the role of ‘waste’

The experiment performed was to construct a large number of Boolean networks containing only twelve nodes, each having a random rule (or transition function) associated with it, and two inputs. Each network is then reduced using the algorithm reported in Richardson (2005) so that the resulting network only contains relevant nodes. Networks of different sizes resulted and their proportion to the total number of networks tested was plotted. Figure 3 shows the frequency of different sizes of reduced network.

If we take an average of all the networks we find that typically only 58% of all nodes are relevant. This would suggest a one hundred - fifty eight principle (as 100% of functionality is provided by 58% of the network’s nodes), but it should be noted that this ratio is not fixed for networks of all types - it is not universal. This is clearly quantitatively different from the eighty-twenty ratio, but still implies that a good proportion of nodes are irrelevant. What do these so-called irrelevant nodes contribute? Can we really just remove them with no detrimental consequences? A recent study by Bilke & Sjunnesson (2001) showed that these supposedly irrelevant nodes do indeed play an important role.

One of the important features of Boolean networks is their intrinsic stability, i.e., if the state of one node is changed/perturbed it is unlikely that the network trajectory will be pushed into a different attractor basin, i.e., its trajectory will be qualitatively unaffected. Bilke & Sjunnesson (2001) showed that the reason for this is the existence of the, what we have called thus far, irrelevant nodes, or ‘waste’. These ‘frozen’ nodes form a stable core through which the perturbed signal is absorbed much of the time, and therefore has no long term impact on the network’s dynamical behavior. In networks for which all the frozen nodes have been removed, and only relevant nodes remain, it was found that they were much less stable - the slightest perturbation would nudge them into a different basin of attraction, i.e., a small nudge was sufficient to qualitatively change the network’s behavior. As an example, the stability (or robustness) of the network in Figure 1a is 0.689 whereas the stability of its reduced, although functionally equivalent network, is 0.619. The next section discusses the property of dynamical robustness in greater detail.

Dynamical robustness of reduced networks

The dynamical robustness of networks is concerned with how stable a particular network configuration is under the influence of small external perturbations. In Boolean networks we can assess this measure by disturbing an initial configuration (by flipping a single bit) and observing which attractor basin the network then falls into. If it is the same attractor that follows from the unperturbed state then the state is stable when perturbed in this way. An average for a particular state is obtained by perturbing each bit in the state and dividing the number of times the same attractor is followed by the network size. For a totally unstable state the robustness score would be 0, and for a totally stable state the robustness score would be 1. The dynamical robustness of the entire network is simply the average robustness of every state in phase space. This measure provides additional information concerning how state space is connected in addition to knowing the number of cyclic attractors, their periods, and their weights (volume of phase space they occupy).

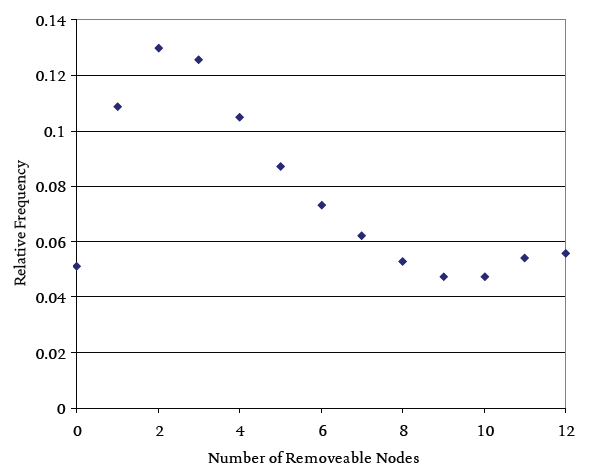
Figure 3

Figure 3 The distribution of reduced network sizes. 100,000 random networks of size N=12, K=2 were generated and reduced to create this data. The average number of removeable nodes is ~5.

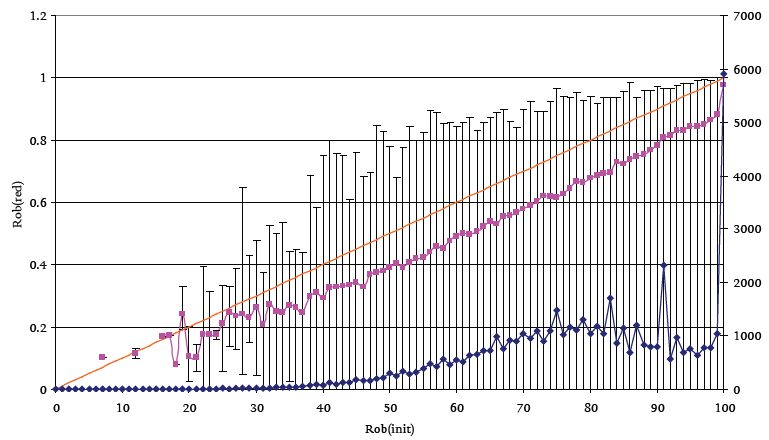
Figure 4

Figure 4 Unreduced robustness versus reduced robustness. The ‘square’ series plots the dynamical robustness (right hand axis), and the ‘diamond’ series shows the number of data points used to create each average (left hand axis). 50000 random networks of size N=12, K=2 were generated and reduced to obtain this data.

Figure 4 shows the relationship between unreduced and reduced robustness for 50,000 small networks whose unreduced size is only 12 nodes (N=12, K=2). The error bars represent the min and max result, and not standard deviations. It is clear that on average the robustness of the reduced networks is noticeably lower than the unreduced networks showing that the reduced networks are rather more sensitive to external perturbations than the unreduced networks. In some instances the robustness of the reduced network is actually zero meaning that any external perturbation whatsoever will result in qualitative change. What is also interesting is that sometimes the reduced network is actually more robust than the unreduced network. Th is is a little surprising, but not when we take into account the complex connectivity of phase space for these networks. Further research aims to confirm these observations in larger networks (there is no reason at all to think that the phenomena will disappear – in fact it is expected to become more marked), as well as to look at the distribution of robustness for each average measurement to confirm that the average is a meaningful measure in this case (which is not always the case in complex systems research).

‘Waste’ provides a container for self-organization

Having consider the process of modularization and the dynamical robustness of complex networks we are now in a position to understand better the role of supposed ‘waste’.

In Boolean networks, each additional node doubles the size of phase space. So even if ‘irrelevant nodes’ contribute nothing to longer term (asymptotic) dynamics, they at least increase the size of phase space. In the example above, the phase space of the initial network is 512 times larger than the phase space of the reduced network. Th us, node removal significantly reduces the size of phase space. As such, the chances that a small external perturbation will inadvertently target a sensitive area of phase space (and therefore pushing the network into a different attractor) are significantly increased. This explains why we see the robustness generally decrease when networks are reduced. Sometimes, however, the robustness can actually increase. This occurs in cases when there is significant change in the relative attractor basin sizes as a result of the reduction process and/or a relative increase in the orderliness of phase space: see example Figure 5 for an example.

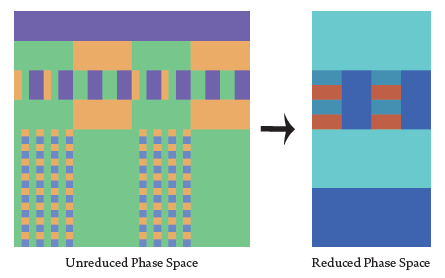
Figure 5

Figure 5 An example of when dynamical robustness actually increases when a complex network is reduced

Prigogine said that self-organization requires a container (self-contained-organization). The stable nodes function as the environmental equivalent of a container. So it seems that, although many nodes do not contribute to the long term behavior of a particular network, these same nodes play a central role as far as network stability is concerned. Any management team tempted to remove 80% of their organization in the hope of still achieving 80% of their yearly profits, would find that they had created an organization that had no protection whatsoever to even the smallest perturbation from its environment – it would literally be impossible to have a stable business.

Not only does ‘waste’ provide a buffer to absorb external perturbations, but it also allows for the emergence of dynamically disconnected modules. The appearance of such modules, or subsystems, is why complex networks do not tend to exhibit ordered or quasi-chaotic dynamics but a more balanced complex dynamics, sometimes referred to as the ‘edge of chaos’. Another way to regard this process is to see the ‘waste’ as creating ‘walls of constancy’ that carve up the network into discrete sub-units, which significantly restrict (but not too much so) the dynamical possibilities of the whole.

Some initial conclusions

So it seems that ‘waste’ really isn’t ‘waste’ afterall. Some tentative conclusions that might be drawn from this initial research are:

Given these conclusions it would, for example, be unwise to continue to regard ‘junk’ DNA as really ‘junk’! At the very least a high percentage of junk DNA would act as a built-in protection mechanism against environmental perturbations, but would also allow for the emergence of a coherent entity (through the process of modularization) rather than a mish mash of randomly allocated cells. If no other role for junk DNA was found (which is rather unlikely) this alone would make its inclusion very important indeed.

References

Bastolla, U. and Parisi, G. (1998). “The Modular Structure of Kauffman Networks,” Physica D, ISSN 0167-2789, 115: 219-233.

Bilke, S. and Sjunnesson, F. (2002). “Stability of the Kauffman model,” Phys. Rev. E, ISSN 1063-651X, 65: 016129.

Kauffman, S. A. (1993). The Origins of Order: Self-Organization and Selection in Evolution, New York, NY: Oxford University Press, ISBN 0195058119.

Richardson, K. A. (2005). “Simplifying Boolean networks,” accepted for publication in Advances in Complex Systems, ISSN 0219-5259.

Sulis, W. H. (2005). “Archetypal Dynamical Systems and Semantic Frames in Vertical and Horizontal Emergence,” in K. A. Richardson, J. A. Goldstein, P. M. Allen and D. Snowden (eds.), E:CO Annual Volume 6, Mansfield, MA: ISCE Publishing, ISBN 0976681404, pp. 204-216.

Kurt A. Richardson is the Associate Director for the ISCE Group and is Director of ISCE Publishing, a new publishing house that specializes in complexity-related publications. He has a BSc(hons) in Physics (1992), MSc in Astronautics and Space Engineering (1993) and a PhD in Applied Physics (1996). Kurt’s current research interests include the philosophical implications of assuming that everything we observe is the result of complex underlying processes, the relationship between structure and function, analytical frameworks for intervention design, and robust methods of reducing complexity, which have resulted in the publication of over 25 journal papers and book chapters. He is the Managing/Production Editor for the international journal Emergence: Complexity & Organization and is on the review board for the journals Systemic Practice and Action Research, Systems Research and Behavioral Science, and Tamara: Journal of Critical Postmodern Organization Science. Kurt is the editor of the recently published Managing Organizational Complexity: Philosophy, Theory, Practice (Information Age Publishing, 2005) and is co-editor of the forthcoming books Complexity and Policy Analysis: Decision Making in an Interconnected World (due May 2006) and Complexity and Knowledge Management: Understanding the Role of Knowledge in the Management of Social Networks (due October 2006).