A STATISTICAL CONSEQUENCE OF THE LOGICAL CALCULUS OF NERVOUS NETS1 [52]
H.D. Landahl, W.S. McCulloch and W. Pitts
A formal method is derived for converting logical relations among the actions of neurons in a net into statistical relations among the frequencies of their impulses.
Consider the neuron cn upon which c1, …, cp have excitatory, and cp+1, …, cp+q inhibitory synapses. Let δ be the period of latent addition, so that cn is excited at the time t if and only if the number of impulses along c1, …, cp which have concurred within an interval of duration δ about t−1 exceeds θn and none has occurred within δ along any of cp+1, …, cp+q. Suppose that the sequences of impulses along c1, …, cp are statistically independent, and let νi be the mean frequency of impulses along ci. Then the mean proportion of time that exactly r excitatory impulses arrive upon cn within an interval of duration δ is given by
Consequently, the mean proportion of time Κ that the number of impulses concurring upon cn within δ exceeds θn is obtained by summing (1) from r = θn to r = p. The intervals of duration δ within which impulses from any of cp+1, …, cp+q occur are intervals when cn is inexcitable. The mean proportion of time when this is not the case is given by
The frequency νn is then the product of (2) by Λ, or
If we compare equation (3) with expression (1) of the preceding paper(1), whose notation we shall use, and apply a straightforward inductive argument, we obtain the following
Theorem.
Let 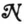 be a net of order zero, or, more generally, one for which
be a net of order zero, or, more generally, one for which
Ni(z) = Si [i = 1, … , s]
is a solution wherein the Si fulfill the conditions of Theorem X of the preceding paper. Let νj be the mean frequency of impulses in cj, and let the expression Ai be generated out of Si by the following rules:
- Replace each N of Sᵢ by ‘δ ν’ with the same subscript.
- Replace every v by ‘ + ’, every · by ‘ × ’ and every ∾ by ‘1—’.
- Replace the operators (zi) and (Ezi) respectively by and wherever they occur.
- Replace every occurrence of a predicate Cmn by a symbol for the function fmn (t) which is defined for all natural numbers t as unity when t = m (mod n), and otherwise zero.
Then the frequencies of impulses in the ci are given in terms of those of the peripheral afferents by the equations
The correspondence expressed by this theorem is exactly that of Boole between the algebra of logic and that of probability. It connects the logical calculus of the preceding paper with previous treatments of the activity of nervous nets in mathematical biophysics and with quantitatively measurable psychological phenomena. For these phenomena we can construct hypothetical nets by the powerful methods of the preceding calculus. The theorem then enables us to determine specific predictions from the quantitative characters of the stimulus to those of the response. These predictions can be compared with observations and, if necessary, the nets be altered until the consequent predictions are verified.
But this procedure leads to error whenever the assumptions leading to equation (3) are not fulfilled. This will be the case if the frequencies are too great, but the limit is many times the maximum observed. When the frequencies are too small, the statistical treatment, though valid, is of little help, but we may here conveniently use the logical calculus directly. The same obtains in microscopic physiological analysis. The most important exceptions are those which arise from physiological factors that synchronize activities and thus restrict the domain of the validity of the assumption of statistical independences required in the derivation of equation (3).
Footnote
Literature
McCulloch, Warren S. and Walter Pitts. 1943. “A Logical Calculus of the Ideas Immanent in Nervous Activity.” Bull. Math. Biophysics, 5, 115-133.
For further research:
Wordcloud: Activity, Along, Biophysics, Calculus, Consequent, Delta, Duration, Equation, Excitatory, Expression, Following, Frequencies, Fulfill, Given, Impulses, Interval, Kern, Limits, Logical, Mathop, Mkern, Mu, Nervous, Nets, Number, Observed, Obtain, Occur, Paper, Phenomena, Pi, Pitts, Preceding, Predictions, Proportion, Quantitative, Relations, Replace, Sigma, Statistical, Theorem, Zero
Keywords: Impulses, Relations, Science, Theorem, Nets, Neurons, Method
Google Books: http://asclinks.live/0pdr
Google Scholar: http://asclinks.live/leqn
Jstor: http://asclinks.live/9ayp