ANASTOMOTIC NETS COMBATING NOISE12 [160]
W.S. McCulloch
##
We inherited from Greek medicine a recognition that knowledge depends in some manner upon a mixture of a knower and the known. The Fathers of Medicine supposed that this mixing took place locally in the anastomotic veins and was carried by the blood to the general mixture in the heart. Except for a few chemical messengers like hormones, we have abandoned this cardiocentric theory of knowledge for a cephalocentric one. We have replaced their mixture of substances with an interaction of signals, but have retained the essentially anastomotic quality of the net. In fact, we conceive our nervous system to be so anastomotic that every efferent peripheral neuron can be affected over a multiplicity of paths by every afferent peripheral neuron.
For the purposes of this paper, I shall ignore all other sources of reliability in the process of perception. I mean such things as: 1) closed loops of reflexive and regulatory mechanisms; 2) use of topological mapping to preserve local sign; 3) redundancy of code that is inherent in the repetition rate characteristic of those nervous structures that determine posture and motion; and 4) autocorrelation functions of the cerebellum that are used to raise signals out of a background of noise.
I shall say nothing about evolution, adaptation, learning, or repair. My reason is this: The nervous system is state-determined; that is, at any one time its change into another state is determined only by the state in which it is and by the input to that state. Consequently, we do not care how it came to be in that state.
For our problem of the moment, perception, we shall deal only with essentially synchronous signals to a layer of neurons whose axons end on the succeeding layer, for as many layers in depth as we choose. Such a net can be designed to compute in any layer at any one time as many Boolean functions of its simultaneous inputs as there are neurons in that layer, and no others. We shall not consider any other nets. We shall suppose that our nets have been designed so that functions computed by the output neurons lead to those responses that are most useful to the organism. This assumption simplifies our problem.
Some twenty years ago, when Walter Pitts and I began our study of a logical calculus for ideas that are immanent in nervous activity, there was good evidence that a neuron had a threshold in the sense that it would fire if adequately excited; that impulses from separate sources, severally subthreshold, could add to exceed the threshold; and that the neuron could be inhibited. For simplicity, we took inhibition as being absolute. These few properties served our purpose, which was to prove that a net of such neurons could compute any number that a Turing machine could compute with a finite tape. Some five years later, these properties sufficed for a theory of how we can perceive universal, such as a chord, regardless of key, or a shape, regardless of size. These two papers were crucial in the development of Automata Theory.
But, ten years ago the inadequacy of these assumptions came to light, theoretically, in von Neumann's paper on probabilistic logic concerned with building reliable computers from less reliable components.
By that time spontaneously active neurons had been demonstrated in most parts of the mammalian nervous system. Inhibitions, like excitations, had been found to sum, and we had come to grips with those interactions of axons that are afferent to a cell and by which signals in one prevent signals in another from reaching the recipient neuron.
We could demonstrate this interaction as peripherally as the primary bifurcation of afferent peripheral neurons. In Nature (January 6, 1962), E. G. Gray has published the first electron microscopic anatomical evidence of axonal terminations upon boutons of other axons, which may account, as proximally as possible, for the interaction.
Interaction of afferents is of great theoretical importance. First, it enables a neuron to compute any Boolean function of its inputs, i.e., to respond to a specified set of afferent impulses, not merely those functions available to so-called threshold logic; and, second, it permits a neuron to run through all possible sequences of functions as its threshold is shifted.
The first is of great importance in audition. The Boolean function is an exclusive OR, and the important cells are in the superior olive. Each cell will respond to an impulse from either ear unless there is one from the other, but never to both or neither. The utility of this arrangement is obvious to anyone with wax in one ear. Put on a pair of earphones with a beep in one ear and drown it 10 decibels under with noise. Next, put the same noise into the other ear also, and the beep is as loud and clear as it is without the noise. Finally, put that beep into the other ear also and it disappears, for it is 10 decibels below the noise. Please note that this noise is external to the central nervous system and is not the kind that we shall consider later.
The second, or sequence of functions determined by shifting threshold, is of great importance in respiration but is not so easily stated. As nearly as I can tell from old experiments and from the literature, the rise in threshold to electrical stimulation that is due to ether is approximately the same in all neurons; yet the respiratory mechanism continues to work under surgical anesthesia when the threshold is raised, at least in cortex and cord, by approximately 200 per cent. The input-output function of the respiratory mechanism remains reasonably constant, although the threshold of its component neurons has changed so much that each is computing a different function (or responding to a different set) of the signals it receives. Von Neumann called such nets “logically stable under a common shift of threshold,” and Manuel Blum has cleaned up the problem for appropriate nets of neurons with any number of inputs.
To explain this, I would like to introduce to you the only symbols with which I have been able to teach the necessary probabilistic logic. I use a X with a jot for true, a blank or 0 for false, a dash for “I don't care which,” and a p for a 1 with probability p. For “A alone is true” (i.e., a sign for A alone),  ; for B alone,
; for B alone,  ; for both,
; for both,  ; and for neither,
; and for neither,  . Then I can write the sixteen logical functions, or firing diagrams, of a neuron with two inputs, as shown in Figure 1, and we can draw the diagrams, as in Figure 2, to show how the computed function depends upon the threshold θ.
. Then I can write the sixteen logical functions, or firing diagrams, of a neuron with two inputs, as shown in Figure 1, and we can draw the diagrams, as in Figure 2, to show how the computed function depends upon the threshold θ.

Figure 1.
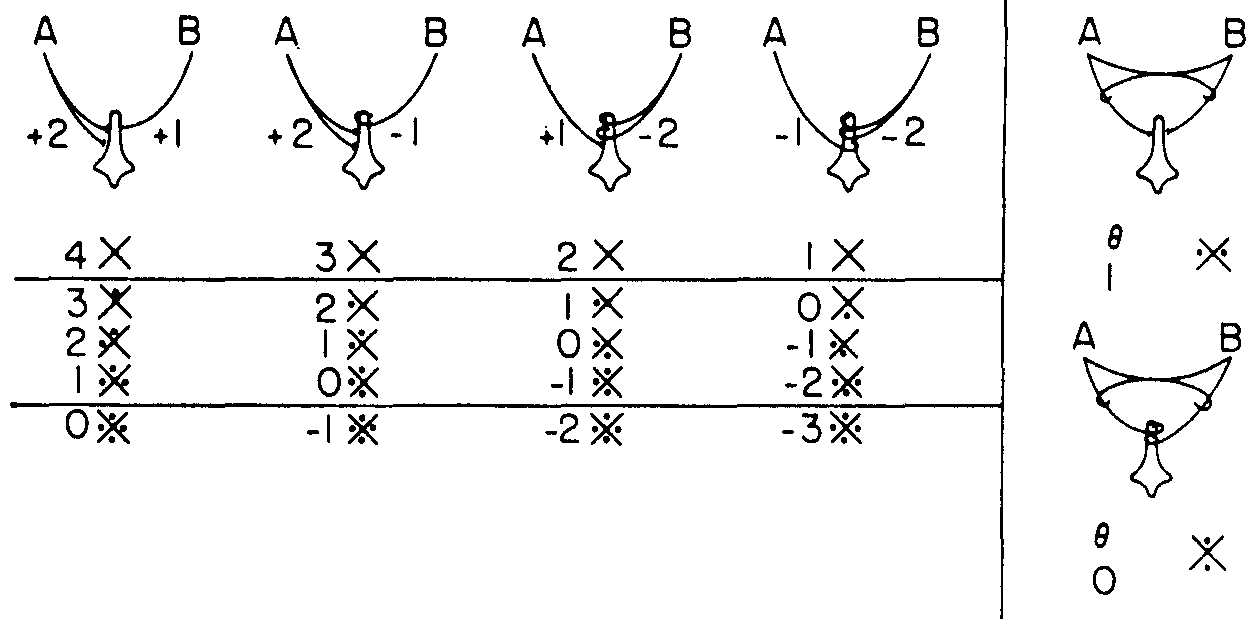
Figure 2.
You will note that the first four neurons, without interaction of afferents, compute all but two of the sixteen logical functions, and these missing ones can be computed by the two neurons at the right in Figure 2. The upper right neuron does the trick in the superior olive.

Figure 3.
To explain respiration, we now use a net of three neurons (Fig. 3), and suppose that we want  ,
,
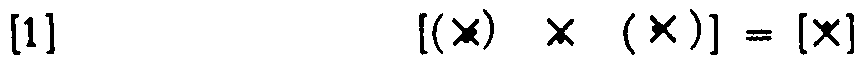 or,
or,
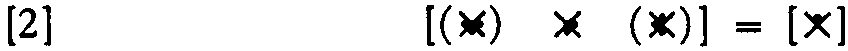
and compute it as in Equation 1, and then decrease every θ by one so as to compute the same  , Now every component is computing a new function of its input; hence, this net is logically stable under common shift of θ over a change of one step. If we were to carry it a second step, we would have a net that always fires or never fires.
, Now every component is computing a new function of its input; hence, this net is logically stable under common shift of θ over a change of one step. If we were to carry it a second step, we would have a net that always fires or never fires.
The maximum range for neurons with two afferents is clearly two steps, but it can only be achieved by nets with interaction of afferents, and then it can be achieved always and for any number of afferents per neuron. For example, Figure 4 shows these expressions
Figure 4.
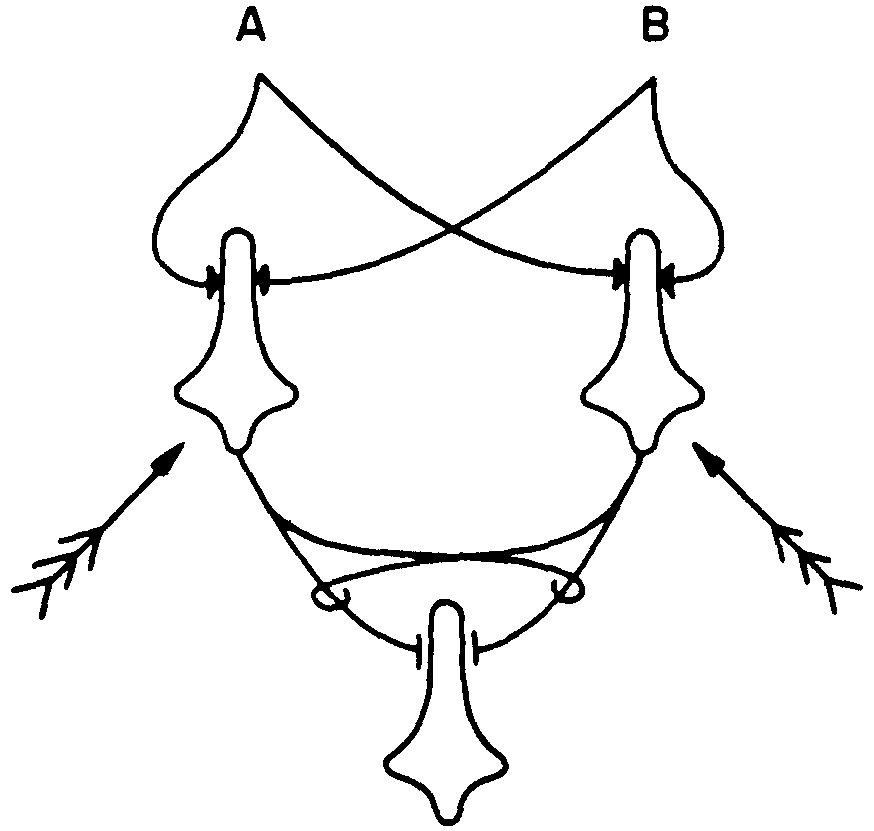
Figure 5.
for a net of three neurons whose output neuron goes through  and requires interaction, as does the left-hand neuron. Obviously no more is possible, for the output would always or never fire.
and requires interaction, as does the left-hand neuron. Obviously no more is possible, for the output would always or never fire.
One more trick served by interaction is the use of separate shifts in θ that are produced by feedback to secure flexibility of function. Consider the net of Figure 5 in which the feathered arrows indicate feedback affecting θ's. This net can be made to compute fifteen out of the sixteen possible functions. Had I drawn it for neurons with three inputs each, it could have been switched so as to compute each of 253 out of the 256 logical functions of three arguments. I strongly suspect that this is why we have in the eye some 100 million receptors and only approximately one million ganglion cells, but note that it depends upon interaction of afferents.
Finally, Manuel Blum has recently proved that this interaction enables him to design nets that will compute any one specified function of any finite number of inputs with a fixed threshold of the neuron at a small, absolute value, say, 1 or 0. This prevents the neuron from having to detect the small difference of two large numbers, thus allowing the brain a far greater precision of response to many inputs per neuron, despite a fluctuation of a given per cent of the threshold θ. This fluctuation of θ is the first source of noise which I wish to consider.
The effective threshold of a neuron cannot be more constant than that of the spot at which its propagated impulse is initiated. This trigger point is a small area of membrane, with a high resistance, and it operates at body temperature. It is, therefore, a source of thermal noise. The best model for such a trigger is the Node of Ranvier, and the most precise measurements of its value are those of Verveen. For axons ∼4µ in diameter, he finds it to be ∼ ±1 per cent of θ; it is larger for small axons. Moreover, his analysis of his data proves that the fluctuations have the random distribution expected of thermal noise. There are, of course, no equally good chances to measure it in the central nervous system, for one cannot tell how much of a fluctuation is due to signals or to stray currents from other cells. Our own crude attempt on the dorsal column of the spinal cord indicates far greater noise, but not its source.
What goes for thresholds goes, of course, for signal strength; and for fine fibers, say, 0.1 µ, the root mean-square value of the fluctuation calculated by the equation of Fatt and Katz is ∼0.5 mv. If we accept a threshold value of 15 mv., this is several per cent. It may be much larger.
Moreover, it is impossible that the details of synapsis are perfectly specified by our genes, preserved in our growth, or perfected by adaptation. They are certainly disordered by disease and injury.
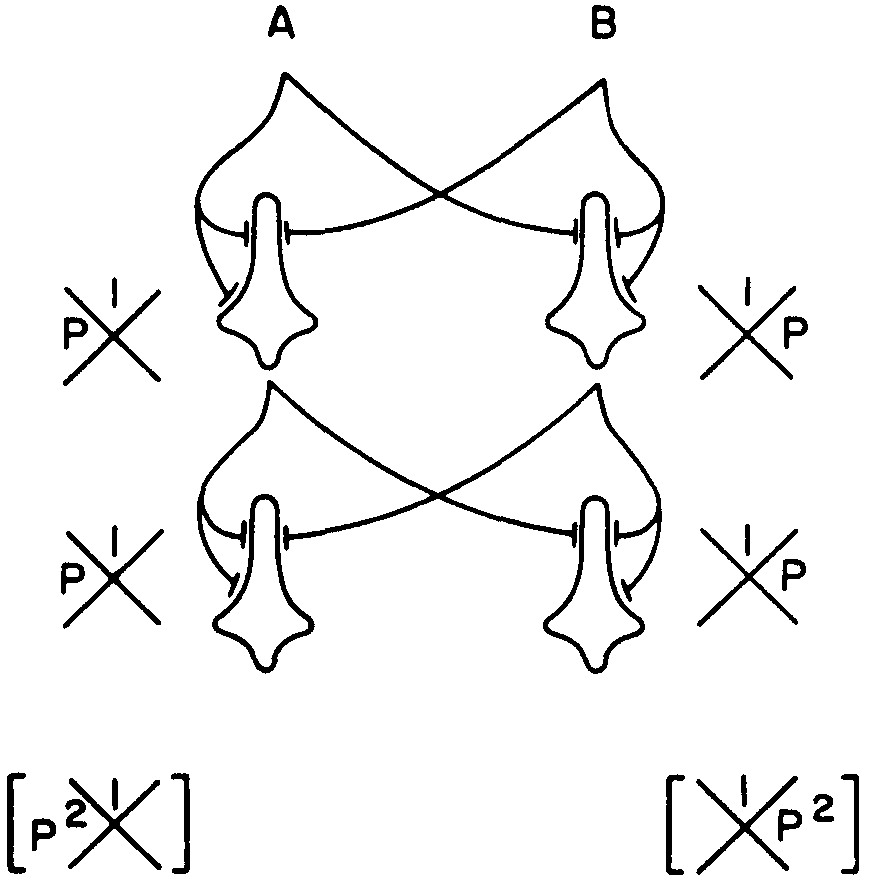
Figure 6.
Nevertheless, it is possible to cope with these three kinds of noise—θ, signal, and synapsis—as long as the output of a neuron depends, in some fashion, on its input by an anastomotic net to yield an error-free capacity of computation. This is completely impossible with neurons having only two inputs each. The best we can do is to decrease the probability of error. Consider, for example, a net like that of Figure 6 to compute  , where each neuron is supposed to have θ = 3, but each drops independently to 2 with a frequency p. As long as p is less than 0.5, the net improves rapidly as the product of the p's of successive ranks decreases. The trick here is to segregate the errors.
, where each neuron is supposed to have θ = 3, but each drops independently to 2 with a frequency p. As long as p is less than 0.5, the net improves rapidly as the product of the p's of successive ranks decreases. The trick here is to segregate the errors.
The moment we look at neurons with three inputs, the picture changes completely; but to describe this change we need to increase the complexity of our logical symbols by putting a circle on the X, so that inside it is C, outside not C, as in Figure 7(a). Now consider a net to compute some function, say, all or else none. We can schematize this, as in Figure 7(b). The dash is a “don't-care” condition; it may be a 1, or 0, or any p that you choose. This net makes no mistakes. Let us suppose that each of the first rank
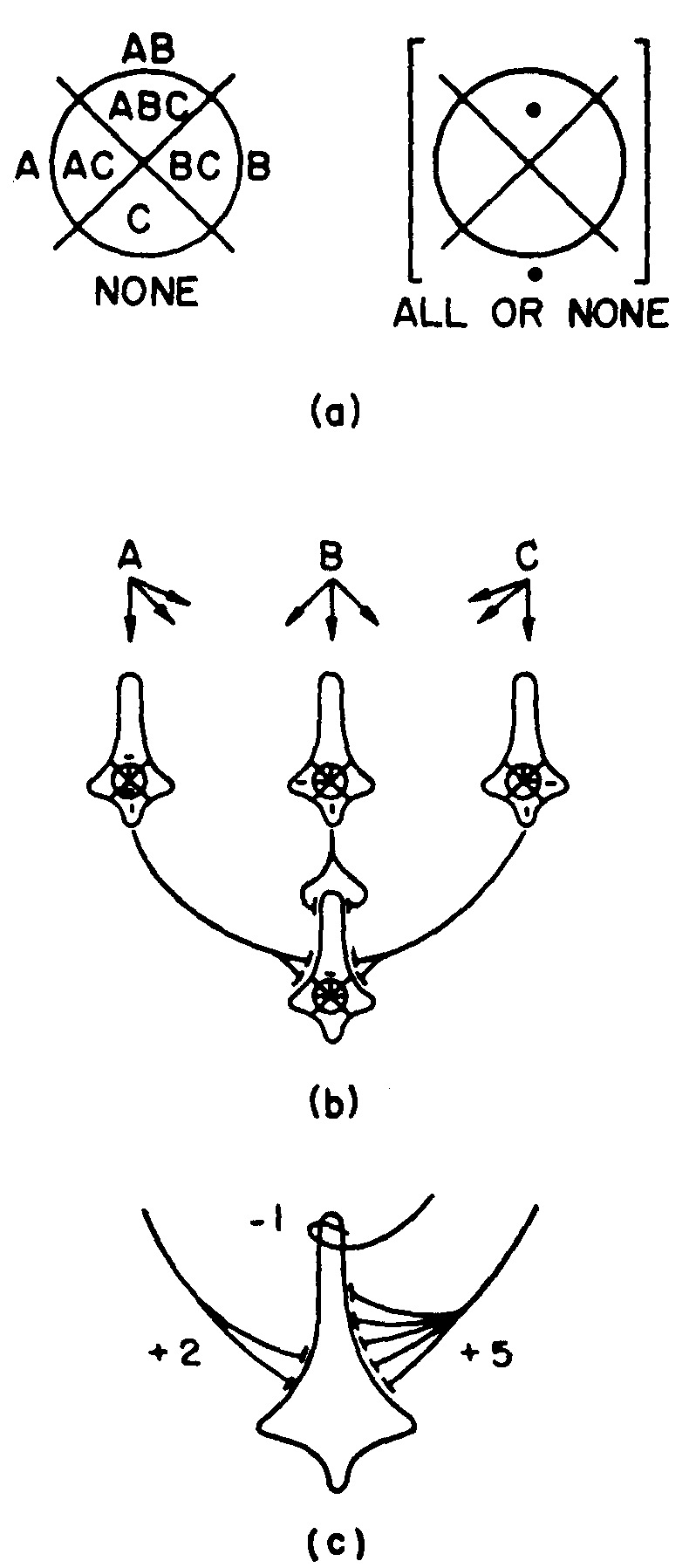
Figure 7.
exerts +2 excitation on the third. Then its threshold can vary harmlessly: 3 < θ < 6, or nearly 50 per cent. Moreover, if the threshold is better controlled, then the strength of the signals can vary. Finally, if both are fairly well controlled, the connections can be wrong, as in Figure 7(c), and the input-output function 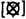 is still undisturbed.
is still undisturbed.
If we want to extend our symbols to four arguments, then the pattern becomes that of Figure 8, and for five arguments it becomes more complex. In general, each new line must divide all existing areas into two; thus for N inputs there are 2N spaces. Oliver Selfridge and Marvin Minsky have worked out simple ways of making such symbols, with sine waves, for any finite number of inputs.
Eugene Prange has invented a way of devising the distribution of don't-care conditions so that there are as many as possible for a net of N neurons in the first rank and one in the output rank, each rank having N inputs per neuron. The number of don't-care conditions, or dashes, depends upon the number of ones in the spaces for the function to be computed. The dashes are fewest when the function to be computed has exactly one-half its spaces filled with ones. Manuel Blum has solved the following questions: 1) Suppose that there are no don't-care conditions, or dashes, in the symbol for the output neuron; what fraction of the spaces for each neuron of the first rank can have dashes and the calculation be error-free for the toughest function (half-filled with ones), all as a function of N?; 2) With all those dashes in the first rank, what
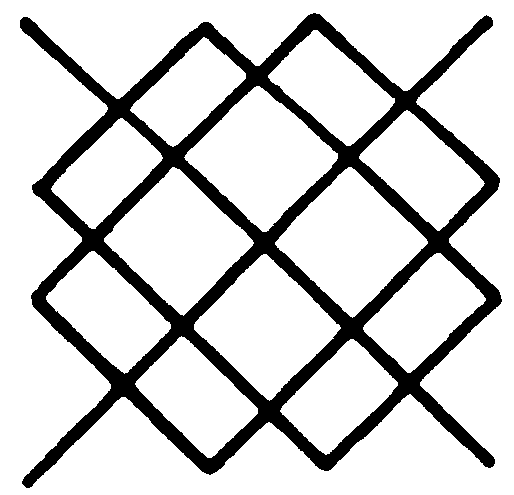
Figure 8.
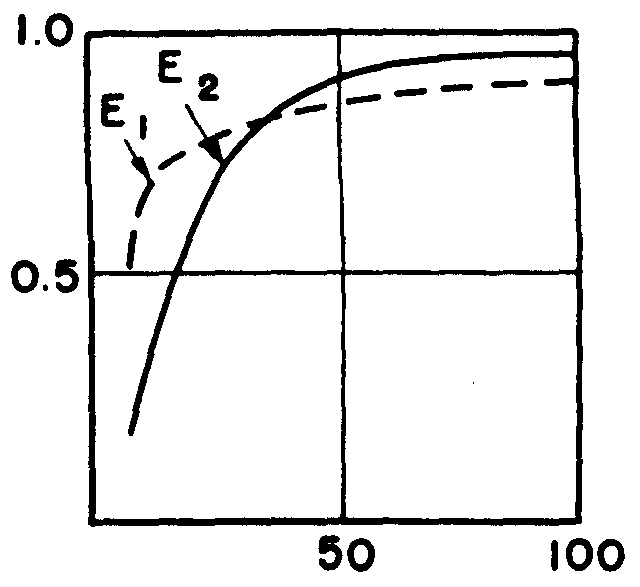
Figure 9.
fraction of the spaces in the symbol of the output neuron can harmlessly be dashes? Figure 9 is Blum's diagram, based on equations that are exact if N is a perfect square and fairly good approximations for the rest.
You will notice that for N less than 40, the output neuron (the solid line) has fewer dashes. At ∼40 they are equal, being ∼80 per cent of all spaces. For larger N, the output neuron has the larger fraction; and, for N = 100, 90 per cent of spaces in the input rank are dashes, and 98 per cent in the output neuron are dashes. From this outcome, it is very clear that the output neuron cannot be a majority organ like the one for N = 3.
We all know that real nervous systems and real neurons have many other useful properties. But I hope I have said enough to convince you that these impoverished formal nets of formal neurons can compute with an error-free capacity despite limited perturbations of thresholds, of signal strength, and even of local synapsis, provided the net is sufficiently anastomotic. If I have convinced you, it has been in terms of a logic in which the functions, not merely the arguments, are only probable. But even this probabilistic logic, for all its don't-care conditions, is adequate to cope fully with noise of other kinds. Our neurons die—thousands per day. Neurons, when diseased, often emit long strings of impulses spontaneously and cannot be stopped by impulses from any other neurons. And, finally, axons themselves become noisy, transmitting a spike when none should have arisen or failing to transmit one that they should have transmitted.
To handle these problems in which the output of a neuron has ceased to be any function of its input, von Neumann proposed what is called “bundling.” In the simplest case, one replaces a simple axon from A by two axons in parallel. This alters the logic, for now if all fibers in the bundle fire, A is regarded as certainly true; if none fire, as certainly false; but between these limits there is a region of uncertainty—call it a set of values between true and false. In the simplest case, there are two such intermediate values. Von Neumann found that if there are only two inputs per neuron, the neurons had to be too good and the bundles too big. To compute, say,  or
or  , with a net constructed like the net of Figure 10, we find that given a probability of an error on the axon, say,
, with a net constructed like the net of Figure 10, we find that given a probability of an error on the axon, say,

Figure 10.
ϵ = 0.5 per cent, to have the bundle usably correct all but once in one million times, he needed 5000 neurons and two more ranks of 5000 to restore his signal so that it was usable. His difficulty was chiefly the poverty of the anastomosis. We have found that, with the same ϵ and the requirement that the bundle be usably correct all but once in one million times, if each axon is connected to every neuron, we only need one rank of 10 neurons.
Leo Verbeek has looked into the problem of the death and fits of neurons, and has found that again the probability of an erroneous output decreases as the number of inputs per neuron and the width of the first rank (both δ in number) increase, at least for probabilities of death and fits reasonably under 50 per cent. Figure 11 shows his graph, where δ is the number of inputs, p the probability of error in the input neurons, and αS(p) the probability of erroneous output. Even for a small δ, these calculations are enormously laborious.
We are all much indebted to Jack Cowan for our knowledge of many-valued logic for handling bundling, and for conclusive evidence that this is not the cleverest way to obtain reliability. He and Sam Winograd have made a much greater contribution, which I could not expound to you if I wanted to, and I do not because it will probably be communicated in full by Professor Gabor for publication in the Philosophical Transactions. Vaguely, its purport is this:

Figure 11.
In the theory of information concerned with communication, there is a theorem, due to Shannon, that, by proper encoding and decoding, if one transmits at something less than the capacity of a noisy channel, one can do so with as small a finite error as one desires by using sufficiently long latencies. Except for things like  and
and  , no one before Cowan and Winograd was able to show a similar information-theoretic capacity in computation. They have succeeded for any computation and for any depth of net, limited only by the reliability of the output neurons. The trick lay in a diversification of function in a net that was sufficiently richly interconnected. Their fundamental supposition is that with real neurons the probability of error on any one axon does not increase with the complexity of its neuron's connections. The recipients of most connections are the largest and, consequently, the most stable neurons. Again, it is the richest anastomosis that combats noise best.
, no one before Cowan and Winograd was able to show a similar information-theoretic capacity in computation. They have succeeded for any computation and for any depth of net, limited only by the reliability of the output neurons. The trick lay in a diversification of function in a net that was sufficiently richly interconnected. Their fundamental supposition is that with real neurons the probability of error on any one axon does not increase with the complexity of its neuron's connections. The recipients of most connections are the largest and, consequently, the most stable neurons. Again, it is the richest anastomosis that combats noise best.
Discussion of Chapter XII
Bernard Saltzberg (Santa Monica, California): In the headphone experiment, I assume you used a single noise source which divided its power between the earphones. Was an experiment attempted with two independent noise sources? How did the results come out?
Warren S. McCulloch (Cambridge, Massachusetts): It does not help much. It has to be the same noise. Different noise is no good. What they were trying when I was last involved was lagging one earphone a little behind the other to see what phase difference they could make in it and still have it work. As far as I know, this has not been cleaned up yet.
Gregory Bateson (Palo Alto, California): What is the price of this increased reliability in terms of loss of educability? Obviously, to obtain a new function—a new relationship—out of this net, you have to alter a large number of connections. In a sense, I suspect that the more reliable your new constructions, the more non- educable the net becomes; but I am not a good enough logician to know that this is so.
McCulloch: Look at the flexibility end of it. We have here a neuron with a couple of inputs (A and B) and one output neuron. Let us take the case of three neurons. Incidentally, I cannot build this without the interaction of afferents. I have one output neuron. Now I can send signals back from the central nervous system and tell my eye what it is to look for, what it is to see. You get 256 possible logical functions. You can calculate 253 of them by giving these first rank neurons a nudge on the threshold. Reliability does not mean that the net is inflexible. This is a remarkably flexible device. The flexibility goes up with the anastomosis; it does not go down. That is one of the beautiful things about it. If it was simple majority logic, the situation would be impossible. The stupidest thing to do, so to speak, if you want to get the maximum life out of a rope is to use it until it breaks and then replace it with another one. No mountain climber that I know takes such a chance. The next worse thing is always to stretch two ropes from man to man. What you want is the richness of connections. The dynamics of the picture is beginning to show up, but the mathematics is too complicated for us as yet.
Eugene Pautler (Akron, Ohio): What type of detector would be required to recognize the results of this output—the computations inherent in this output neuron?
McCulloch: I think it is probably all done in the eye. Suppose you tell your eye to look for four-leaf clovers. You simply send out the message, “Find a particular pattern in those leaves”; and when you have found it signal, “Here is one! Here is another!” You knew what you were looking for so you set your filter accordingly.
A frog, when he jumps, sends back impulses to his eye to give as great a response as possible to an affair of lesser curvature or greater radius of curvature, which informs his eye. This works during the first part of the jump while his eyes are open. One tells one's eye what to see, what too look for. It would be almost unthinkable that otherwise one could go into, say, Grand Central Station, look off across the hall, and, knowing that there is a chance of so-and-so being there, find him, unless one has in some manner set a filter. Just how much of that matching is done in the eye, I do not know. The mouse, which does not turn its eyes and keeps them open, is another nice animal to work on. His retina is the same all over, and whether you get a response from a particular ganglion cell or from a particular axon depends upon whether the mouse is hungry or whether it has smelled its cheese. If it has, then it bothers to look, but it will not look the rest of the time. The mouse shows very little response to any visual stimulus. The situation is far too complicated to be solved with a set of electrodes.
Homer F. Weir (Houston, Texas): In the use of the injured neuron, you are apparently producing noise from non-input sources. Is it correct to say that your injured neuron is putting out output without input?
McCulloch: Yes. Either it is doing that or it is dead.
Weir: At what level would this have to occur, relatively speaking, before it would override this protective error mechanism that you were speaking of?
McCulloch: I have not seen my own cerebellum, but I have seen that of many a man my age. I am in my second century, and I expect that at least 10 per cent of the Purkinje cells in my cerebellum are replaced by nice holes at my age, but I can still touch my nose. It is incredible how little brain has to be left in order for it to function.
Footnotes
Acknowledgment
I wish to acknowledge the contributions of those who have worked with me in this endeavor, namely: Anthony Aldrich, Michael Arbib, Manuel Blum, Jack Cowan, Nello Onesto, Leo Verbeek, Sam Winograd, and Bert Verveen.
For further research:
Wordcloud: Afferents, Anastomotic, Axons, Blum, Bundle, Cells, Cent, Change, Compute, Conditions, Connections, Consider, Dashes, Depends, Different, Ear, Error, Eye, Figure, Fire, Function, Impulses, Inputs, Interaction, Logic, McCulloch, Nervous, Net, Neuron, Noise, Number, Output, Per, Possible, Probability, Problem, Rank, Reliability, Response, Signals, Small, Source, Spaces, State, Suppose, Symbols, System, Threshold, Value, Work
Keywords: Nets, Cerebellum, Systems, System, Signals, Net, Structures, Mapping, Things, Veins
Google Books: http://asclinks.live/8hpz
Google Scholar: http://asclinks.live/wtaw
Jstor: http://asclinks.live/p3lu