THE RELIABILITY OF BIOLOGICAL SYSTEMS¹² [149]

J.Y. Lettvin, H.R. Maturana, W.S. McCulloch and W.H. Pitts

I have been working since 1917, in one way or another, on the problem of how man knows a number. For a while I wasted my time in psychology, then in physiology, and then in symbolic logic. Because I could not come to grips with the problem without better knowledge of the human brain, I studied medicine.

The most remarkable thing a doctor ever experiences is to deliver a baby. It comes out a certifiable suckling and it performs this sucking with great precision, although there are a few mistakes. This leads the physician to realize that, on the level of the human life, he is up against an enormously well-organized system that is consequently stable in its performances. So I look at the problem of self-organizing systems somewhat differently from anyone who begins with the presupposition of randomness.

The ultimate particles of physics must fit and stick to make atoms and those atoms must fit and stick to make molecules, and so it goes, up the scale of the natural objects, to the most complicated thing one knows about: man, always with enormously strong, close-range forces binding the parts together.

When we build a gadget out of components, we torture the materials; we lack atomic glues. We deal with large blocks of stuff sawed out like a piece of wood from a tree, where they belonged together, to make a thing, like this table, that couldn't withstand a hurricane for half an hour. The natural thing and the artifact are not alike.

I didn't appreciate how unlike they are even three or four years ago, for I thought of a nerve cell as a bag full of salt water. But now I am convinced that the inside of the nerve cell is as structured as the inside of a paramecium. I do not believe that even the water in it is free. There is no such disorder in it as there is in a solution.

Dr. von Foerster told us that order, whatever else it is, is fundamentally a redundancy of structure; so that which is ordered can be described in a smaller number of terms. That which is redundant is, to the extent that it is redundant, stable. It is therefore reliable. It is only out of redundancy that one can buy security.

I went to M.I.T. to work on the circuit theory of brains because I was convinced that brains are devices for transmitting information. That is the way they have their truck with the totality of the world. Everything else is irrelevant. The physician needs to consider the energetics only when he has to treat an insane man or an epileptic; that is, only when the brain is diseased.

I thought that I would be able, in terms of information theory, to study the redundancies of code and the redundancies of channels, and so on, and simply transfer the proper theorems to the kind of redundancies that are most important in the bulk of the brain. As yet, we don't know all of them. There is redundancy of code and there is redundancy of channel; but there are kinds of stability you can buy with the redundancy of code that you cannot buy with the redundancy of channel, and vice versa. Personally, I have worked only on redundancy of calculation. By that I mean that the information is brought to a lot of so-called neurons, and these crummy neurons, working in parallel computation, can come out with the right answer even though the component neurons are misbehaving. I always expected, and so, I think, did Shannon and Elias, that we would be able to transfer many of our solutions from any one of these fields to the others; but they now appear to be radically different. The reliability you can buy with redundancy of calculation cannot be bought with redundancy of code or of channel.

There is one more type of redundancy I want to speak about for a moment. That is the redundancy of potential command. Until two or three weeks ago I took it for granted that the redundancy of potential command was simply a redundancy of calculation. Now I am sure it isn't. Suppose you have, as you have in your reticular formation, or as you have in a naval fleet, knots of communication in cells or ships and that each of these stations receives information from practically the whole of the organism or the fleet, but no two are coded alike. The information is probably pulse-interval modulated and the signal probably carries the signature of its origin and word of what is going on there. Other stations may receive much the same information differently coded, but there is no assurance that all will get all of the incoming information.

In such a network as the reticular formation in your brain you have a structure in which any small number of cells can actually accumulate the necessary information, and, simply because they have that information, start buzzing. This decides that you attend to something to your right or go out and get your lunch, you go to sleep, or what not. If disease shoots out any particular cell, there are plenty of other cells that have much of the same information. A few of them, agreeing, run the works. Thus we have a redundancy of potential command in which knowledge constitutes authority. This needs study; but not discussion here.

What I shall present to-day is the redundancy of calculation. In it there are ridiculous troubles on account of misbehavior of small whole numbers that have delayed me unduly.

I have worked since 1952 to develop what I will call a probabilistic logic in the sense in which John von Neumann used the phrase. By “ probabilistic logic ” von Neumann did not mean a logical calculus composed of certain functions of arguments which were uncertain—i.e. a calculus of probabilities. He meant a calculus in which the functions were uncertain, whether the arguments were certain or only probable. This, his usage, has nothing to do with multiple truth-valued logics, which I have never found to be of any help in this problem. The neuronal diagrams that he and we have employed are formal devices for arithmetical operations, and their resemblances to real neurons is of no logical significance and only a stimulus to neurophysiological investigation. The neuronal nets are not a development of Birkhoff's lattice theory, and, though they have superficial resemblances, neither has assimilated the other. The operations of these probabilistic symbols upon each other are not simple matrix multiplications.

I have brought you uncorrected copies of my Quarterly Progress Report on probabilistic logic. It constitutes Part B of my presentation. I have also brought you a very rough first draft of the paper I am about to read to you. It will appear in a later Quarterly Progress Report. Call it Part A.

I would like to present the results of half a dozen years of thinking in half an hour. To make it easier for you I have put at your disposal uncorrected copies of both parts of what I am about to say. Both are but continuations of work presented in Teddington under the title, Agathe Tyche.(1) There I described solutions to these problems raised by John von Neumann,(2, 3) as to the action of the nervous system. They are concerned with (1) circuits which have the same output for the same input when all component neurons undergo a common shift of threshold so that each component computes some new function of its input; (2) the design of circuits more reliable than their components; and (3) the nature of neurons that makes them more flexible in computation than any man-made devices.

The symbols used there, and here, to describe the functions computed by neurons are derived from Venn's(4) diagrams for the intersection of classes. In this case, the classes are composed of events each of which is the signal that an event of that class has occurred. When a jot appears in such a diagram in any place it indicates that the neuron whose action it represents is supposed to fire under that condition. Thus each Venn symbol pictures Wittgenstein's Truth Table(5) for that function. Every line in a Venn diagram divides all other spaces into two spaces. Thus the Venn symbol for a neuron with δ inputs has 2^*δ* spaces. Here are my diagrams (Fig. 1).

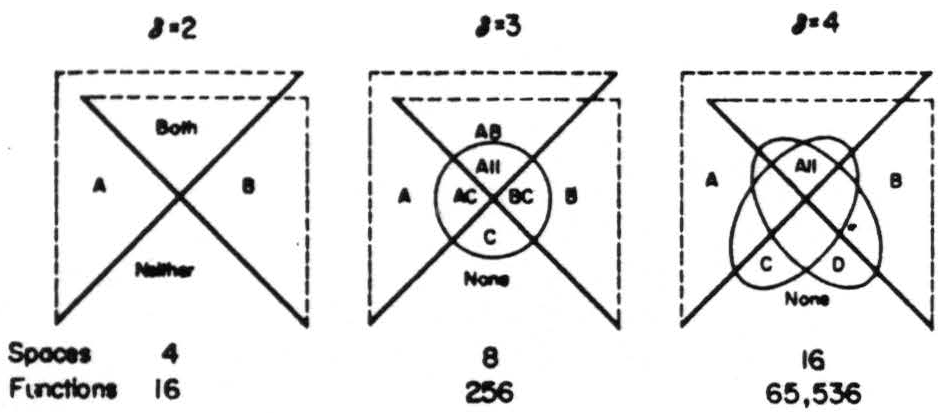
Figure 1. Venn symbols for δ equal to 2, 3 and 4.

For larger δ it is more convenient to use Oliver Selfridge's device consisting of cosine waves each twice the amplitude and half the frequency of its predecessor, so as to generate the sequences of spaces S₀ ${S_{{2^{\delta - 1}}}}$ of Table I of part B. It is only of existential importance in part A, for it allows us to consider δ of any size, though the Venn symbols actually exemplified in it are for δ = 3.

Part A.

Infallible Network of Fallible Neurons

When I presented Agathe Tyche I thought that no circuit could preserve error-free action if it were composed of 3 neurons each receiving only two inputs. To correct this, let me replace the jot in any Venn symbol by 1 if the jot is always present, by 0 if it is always absent, and by p if it is present with a probability p due to a shift of the threshold θ of the neuron it represents. Thus

represents a neuron which always fires when A alone or both A and B occur, and fires with a probability p when B alone or neither

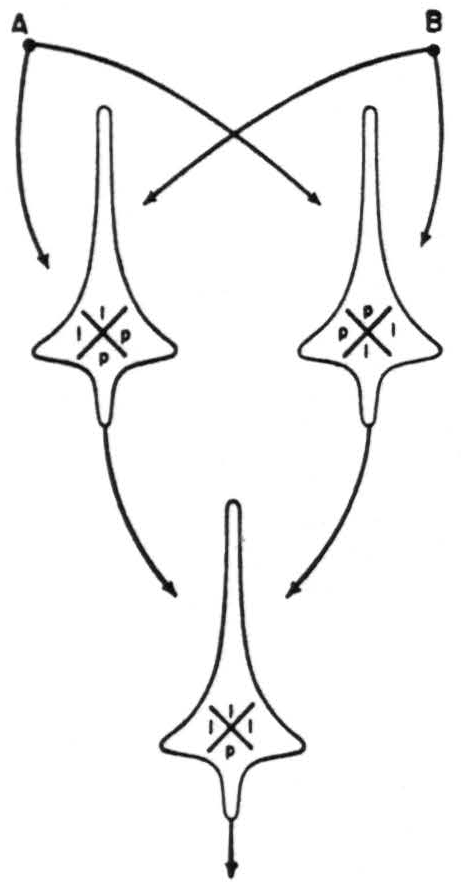
Figure 2. An infallible net of *δ* = 2 neurons.

A nor B occurs. For error-free operation, some spaces in the Venn symbols must have 0 or 1. I place each symbol inside the ideogram of its neuron and draw Fig. 2 in which each of those of the first rank receives signals from A and from B, and both play on the output neuron at the bottom. A formula of the first rank is one whose arguments are independent. A formula of the second rank is made by replacing the arguments with formulas of the first rank. Thus in Fig. 2, the top two neurons are of the first rank and the lower is of the second rank.

For nets of neurons of 2 inputs, i.e. whose δ is 2, zero error can be achieved only for tautology and contradiction with some p in every chi (χ), that is, by keeping the fixed jots or blanks in such positions that, when added, they form tautology or contradiction. But, as the complement of tautology is contradiction and that of contradiction is tautology, these lead only to themselves and to no significant functions of their primitive propositions. I might write this

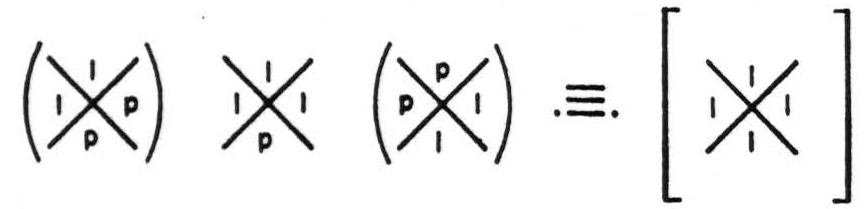
Figure 2a

Thus this circuit always computes tautology, for it fires for any combination of the truth values of A and B. Similarly I may write for contradiction

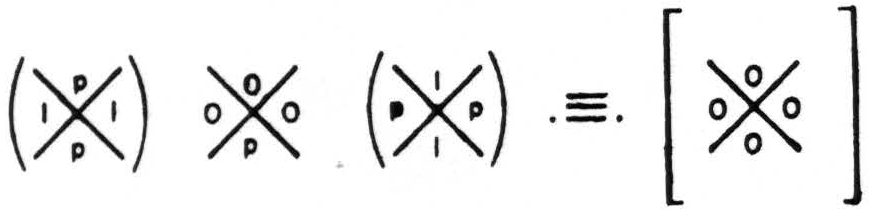
Figure 2b

The two neurons of the first rank need only be such that the ones in each added to those in the other are sufficient to insure a one in every place—i.e. they must be complements under tautology. Yet, since the complement of tautology is contradiction and, of contradiction, is tautology, these are useless for generating any other function free of error. Tautology and contradiction tell us nothing about the world, and it is only these other functions that are significant. I should like to add here that if one is given a single significant function without error one can compute it and its complement without error, using only fallible neurons.

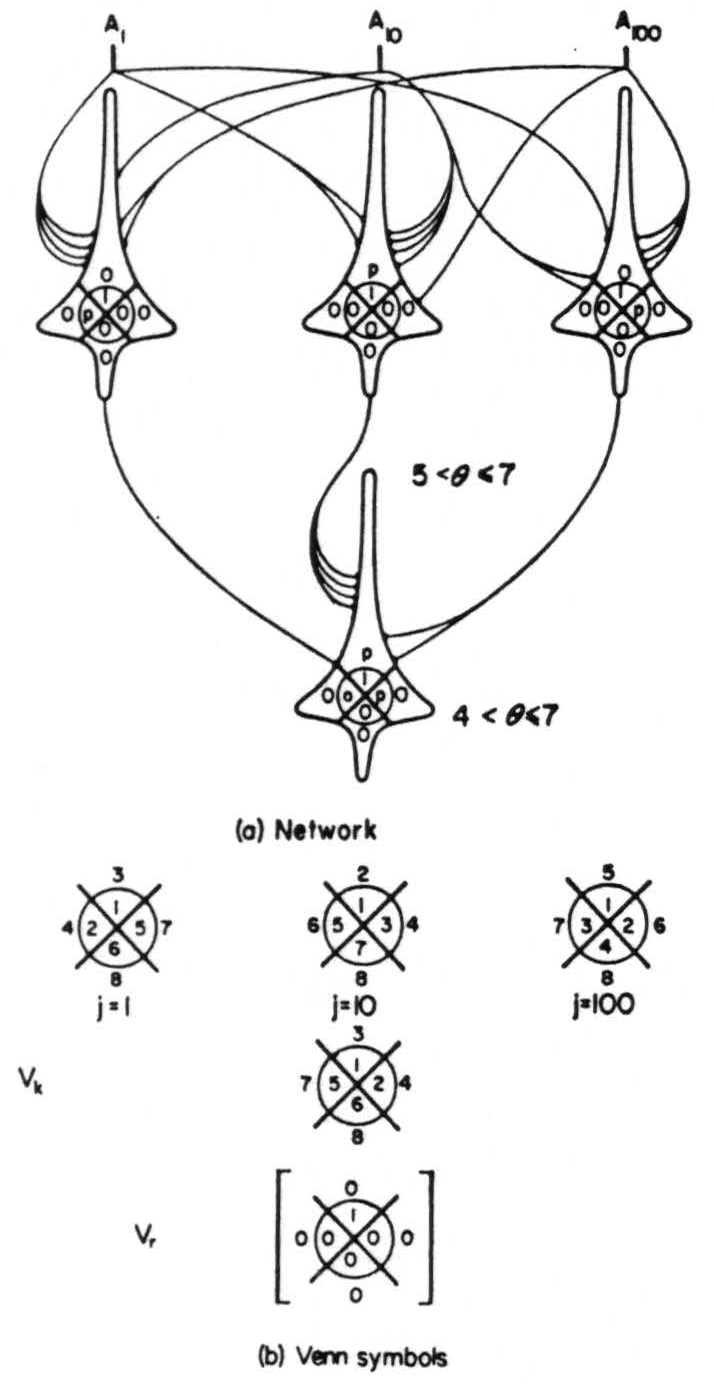
Figure 3. Error-free net of *δ* = 3 neurons.

This limitation disappears with δ = 3. For instance, consider the net of Fig. 3(a) for nondegenerate³ δ = 3 neurons. In Fig. 3(b) are shown the Venn symbols for these neurons with the order in which jots are added as θ decreases indicated—i.e. if θ = 7, the symbol has a jot in position 1; if θ = 6, jots are located in 1 and 2; if θ = 5 they are located at 1, 2, and 3; and so on, until for θ = 0 all eight spaces in the symbol contain jots. The neurons of the first rank will all be certainly fired when all three inputs are present. The first may also be fired by the combination of inputs A₁ and A₁₀₀; the second may be fired by the combination of inputs A₁ and A₁₀; and the third by A₁₀ and A₁₀₀. Thus none of the first rank neurons can be fired by a single input, and furthermore no combination of two inputs can fire more than one. The output neuron will certainly be fired when all three first rank neurons are fired and may be fired by any combination of two of them. However, it has been shown that only the presence of all three inputs A₁, A_l0 and A₁₀₀ will cause more than one of the first rank neurons to fire. Therefore only this combination will result in an output from the net. Thus in each Venn symbol any of the p's can be replaced by a 0 or 1 without affecting the network output of the network.

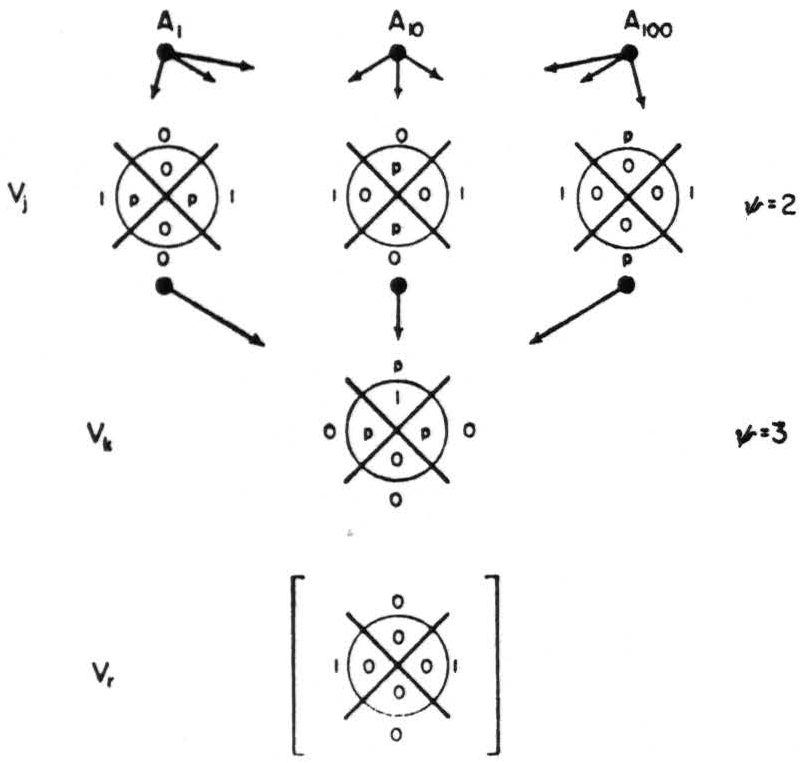
Figure 4. Derivation of an infallible net.

The following algorithm will serve for the derivation of error-free nets when δ is odd. Let J = 2^δ mod δ, and let ψ be the number of jots that may be added harmlessly to the Venn symbol that can stand fewest additions of any Venn symbol in its rank; write the desired function (V_r) of J or fewer jots as 1's in more than half of the V_j. In V_k enter the required 1 in the proper space, and p in all of its other spaces for the intersections of more than half of its arguments (see Fig. 4). There are 2^δ-1 of these spaces, one of which contains the 1: Therefore the number of p's in V_k, call it ψ, is 2^δ-1 − 1.

In every V_j there remain 2^δ − J empty spaces in which p's may be placed if they do not occur in the same space in more than ½(δ − 1) of the V_j. This permits them harmlessly in ½(2^δ − J)(δ − 1)δ ^-1

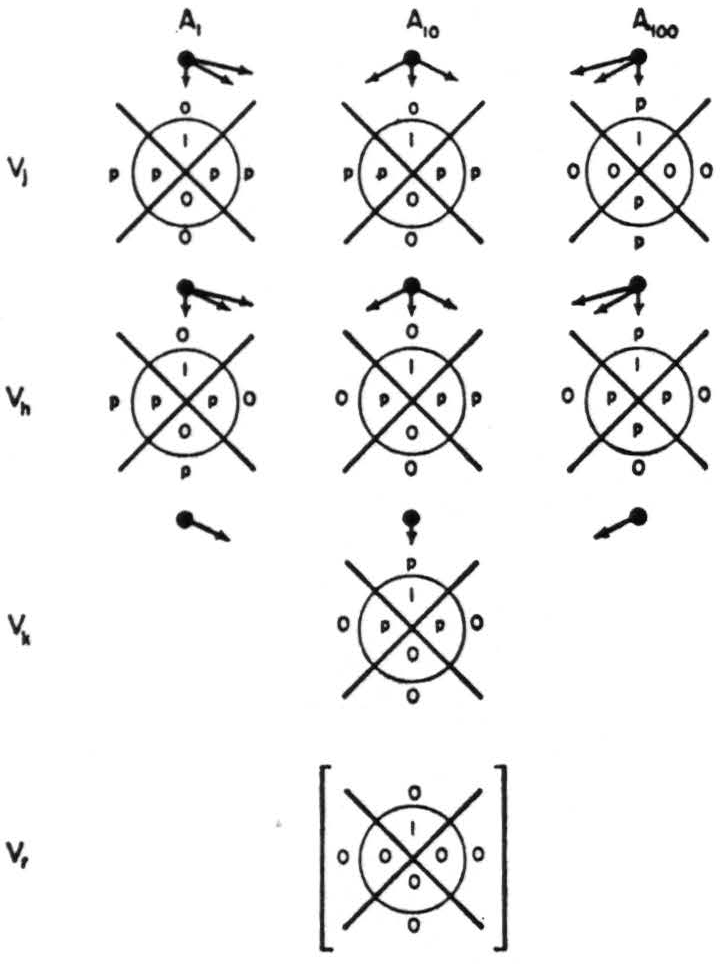
Figure 5. Infallible network with third-rank output neuron.

spaces of each V_j. Now, for δ odd, J is 2 if δ is prime. Harmless p's are most numerous when J is smallest. Hence the maximum ψ_j = (2^δ − 2)(δ^-1)½(δ − 1) = (2^δ-1)(δ − 1)δ^-1.

Writing ψ^* for 2^-δ ψ_max, we have

\psi _k^ * = {2^{ - \delta }}({2^{\delta - 1}} - 1) = \frac{1}{2}(1 - {2^{1 - \delta }});

and

\psi _j^ * = {2^{ - \delta }}{\delta ^{ - 1}}({2^{\delta - 1}} - 1)(\delta - 1) = \frac{1}{2}(1 - {2^{1 - \delta }})(1 - {\delta ^{ - 1}})

Hence,

\;\mathop {\lim }\limits_{\delta \to \infty } {\mkern 1mu} \psi _k^* = \;\mathop {\lim }\limits_{\delta \to \infty } {\mkern 1mu} \psi _j^* = \frac{1}{2}

The binomial coefficient for the central term when δ is even has to be allotted either to the V_j or else to V_k, and its effect diminishes comparatively slowly, without affecting the limits.

Functions of J or fewer 0's can be constructed similarly. Any additional 1 or 0 after J decreases ψ_j by 1, reaching a maximum loss of ½(2^δ − JV_j $\psi _j^ *$ . When not all J are used for 1's or 0's, this space can be occupied in only some of the V_j and so ψ*j is not increased.

For nets with 2 ranks, V_j and V_h neurons, and one third-rank output neuron V_k, ψ_k and ψ_j increase to equal ψ_k for all neurons, and almost all may have one additional p harmlessly as in Fig. 5, where ψ = 3 in V_j=100 and in V_h=10 and in V_k.

We compute the number of nondegenerate infallible nets of two ranks thus: For each V_j there are

{\psi _j}!\left( {{\psi _j}\frac{{\delta + 1}}{{\delta - 1}}} \right)!

which meet the requirements, and for V_k there are

{\psi _k}!\left( {{\psi _k}\frac{{\delta + 1}}{{\delta - 1}}} \right)!

The number of nondegenerate nets is

{\psi _j}!\left( {{\psi _j}\frac{{\delta + 1}}{{\delta - 1}}} \right)!\,\,{\psi _k}!\left( {{\psi _k}\frac{{\delta + 1}}{{\delta - 1}}} \right)!,

second we define the least as x + 1 and suppose that they differ from each other by 1 step in θ. Then

\frac{{\delta + 1}}{2}x + \sum\limits_1^{\frac{1}{2}(\delta + 1)} {{\rm{(integers)}}} > \frac{{\delta - - 1}}{2}x + \sum\limits_{\frac{1}{2}(\delta + 1) + 1}^\delta {{\rm{(integers)}}}

and

x\,\, > \,\,\frac{{\delta + 1}}{2}\left[ {(\delta + 1) - \left( {\frac{{\delta + 1}}{2} + 1} \right)} \right] - \frac{{\delta + 1}}{2},

$\frac{{\delta + 1}}{2}\, \cdot \,\frac{{\delta - 3}}{2}$

Hence the least term is

\left( {\frac{{\delta + 1}}{2}\, \cdot \,\frac{{\delta - 3}}{2}} \right) + 2 = {\left( {\frac{{\delta - 1}}{2}} \right)^2} + 1,

and the greatest is [(δ² $\psi _k^ *$ , is as far from equal strengths as possible. The allowable change in threshold is decreased only by a factor 1/2δ[(δ² − 1)/(δ² + 3)].

For example: if V_k has 7 inputs, each with a value of + 13, its output is error-free for 39 < θ < 91, which is reduced by letting the inputs range from + 10 to + 16 to 45 < θ < 91. Thus the remaining usable range of θ, Δ*θ½ $\psi _k^ *$ = [½ − (1/2⁷)].

Note that if one is willing to forego the possibility of a jot appearing in the position for none in V_k, thus reducing ψ_*k* to [½ − (1/2⁶)], the value of Δ*θ is 66.6% for equal afferents and 56% for afferents ranging from + 10 to + 16.

Since the measured variation, Δ*θ, of real neurons is ±5%, we look next at the permissible independent variation of the strength of afferent signals to V_k, when these strengths were intended to be equal. Clearly, any selection of (δ − 1)/2 signals has a maximum sum less than the minimum sum for δ signals. Let t be the intended strength of a and, for large δ, it is nearly (2^δ-1!)⁴, which is a large number but, divided by the number of all nets, is the negligible fraction

\frac{{{{({2^{\delta - 1}}!)}^4}}}{{{{({2^\delta }!)}^{\delta + 1}}}}

J $({2^{{2^\delta }}} - 4)$ which still leaves it negligible. Chance is unlikely to produce such nets or to discover them among nets supposed equiprobable.

No comparable measures of the number or fraction of diagrams that are degenerate can be similarly computed, either because (1) they do not change the function computed with every step of θ or because (2) they change the symbol by two or more jots per step in d. What misled me in Agathe Tyche was that I had examined only output neuronal diagrams in which δ < 3 and in which there was no inhibition of afferents by afferents, but only a direct action on the recipient neuron, and that, among these, only degenerate diagrams give E_k. Clearly, the degeneracy of the second kind is greatest when all afferents have equal signal strength, and of the first kind when the strength of the afferents goes up maximally between none and the least one, etc. The first kind is therefore minimized by using the smallest whole numbers possible, and the second by having them as unequal as possible.

Since in V_k the spaces for (δ + 1)/2 arguments must be filled before any spaces for fewer arguments are filled, inputs each equal to one would produce the desired result with no degeneracy of the first kind but with maximum degeneracy of the second kind. To minimize the signal and Δt its variation. Then

\sum\limits_0^{\frac{1}{2}(\delta - 1)} {(t + \Delta t)\, < \,\sum\limits_0^\delta {(t - \Delta t)} }

Hence

\frac{{\left| {\Delta t} \right|}}{t}\, < \,\frac{{\delta + 1}}{{3\delta - 1}} = \frac{1}{3}\left( {1 + \frac{4}{{3\delta - 1}}} \right)

which always exceeds ⅓. For example, for δ = 3, with the intended strength, t, equal to 2, we have, 1 < (t ± Δt) < 3. To retain Δθ of ± 5% of its intended value reduces these limits to

1·05 < (t ± Δt) < 2·85, or |Δt|/t = 0·425.

[When a variation of this size is experimentally produced in the afferent termination in the spinal cord of the cat, it alters the circuit action. Even post-tetanic potentiation and convulsive doses of strychnine alter the voltage of signals by less than 10%].

If we hold Δθ to a minimum and the signals to their intended strength, we may permit variation, Δs, in the connections, or synapsis, s, to obtain a similar limit.

\frac{{\left| {\Delta t} \right|}}{s}\, < \,\frac{1}{3}\left( {1 + \frac{4}{{3\delta - 1}}} \right)

$\sum\limits_1^\delta {\left( {s \pm \Delta s} \right) = \delta s;}$ whence

|Δs|/s = δ + 1/δ − 1

whose limit as δ → ∞ is unity. For δ = 3, to the nearest integer, s ± Δs = 2 ± 3 (see V_k of Fig. 6) the range of θ is from (− 1) to (+ 7) and 5 ⩽ θ ⩽ 6, or Δθ = ± 6·25%.

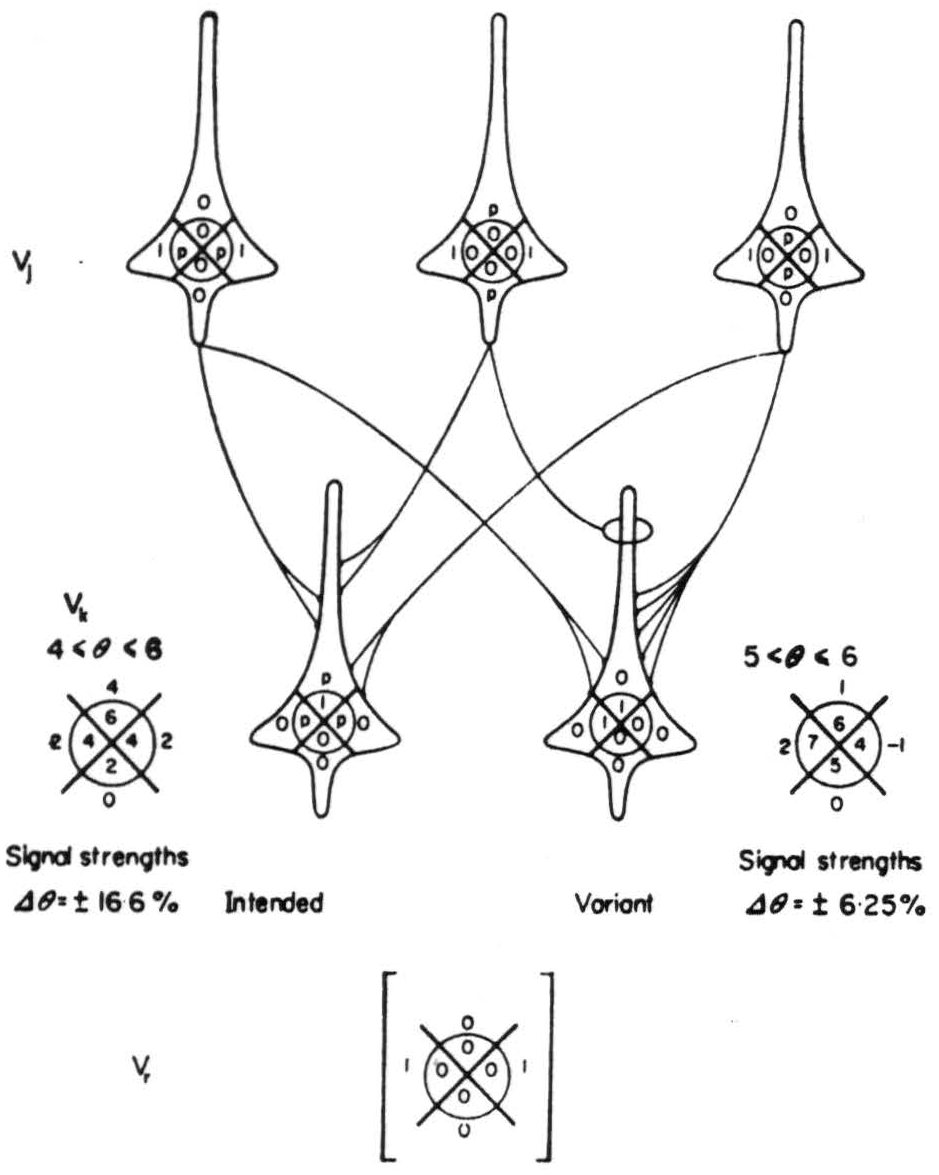
Figure 6. Network illustrating variation in synapsis.

From the preceding paragraphs it is clear that the number of p's that may appear in any Venn symbol for a given change in θ is fixed only for nondegenerate diagrams, and that, for the degenerate diagrams, the fractional change in the jots is generally less than the fractional change in θ. Thus the actual reliability tends to exceed expectation as the specifications of strengths of signals or of coupling (i.e. synapsis) are randomly perturbed. But it would be a work of supererogation to inquire into this in general, for the nature of real or of artificial neurons and the statistical specifications of their connections necessarily determine the weight to be alloted to each factor.

If an educated guess as to real neurons and their nets is now permissible, it must take the general form of a Δθ of ± 5%, a Δt of ± 10%, which leaves Δs, for δ ⩾ 3, less than ± 100% for synapsis for neurons of the second or higher rank. This presupposes that neurons of the first rank are relatively closely specified in synapsis in order to segregate possible errors. This is in harmony with much that is known of the auditory system, wherein pitch, loudness, and direction are initially decoded and thence transmitted over separate channels or in dissimilar codes. It begins to look as though the same were true of vision, of proprioception and of the stages of afferents from the skin following detection and amplification. Thus by the time information from any source reaches our great central computers we are in a region wherein crude specifications of statistical kinds should insure error-free calculation despite gross perturbation of threshold, of excitation, and even of local synapsis. This conclusion follows from two assumptions: first, that we are dealing with a parallel computer of more than two afferents per neuron, and second, that the functions that their neurons compute are sufficiently dissimilar to insure, at at least one level, incompatibility of error in the functions computed. All else may be safely left in large measure to chance.

Part B.

On Probabilistic Logic

Formulae for any logical function of two arguments, and these are the usual ones of symbolic logic, can be reduced to a single Venn symbol by the rules given in Agathe Tyche for operators with jots in x's. It is a special case of what we state here for any number of inputs and for the likelihood, 0 ⩽ p_i ⩽ 1, of a jot appearing in the appropriate space, S_j, of the Venn symbol.

Any statement of the finite calculus of propositions can be expressed as follows. Subscript the symbol for the δ primitive propositions A_j, with j taking the ascending powers of 2 from 2⁰; to 2^δ-1 written in binary numbers, A₁, A₁₀, A₁₀₀, etc. Construct a V table with spaces S_i subscripted with the integers i, in binary form, from 0 to 2^δ− 1 (cf. columns S_i of Table 1).

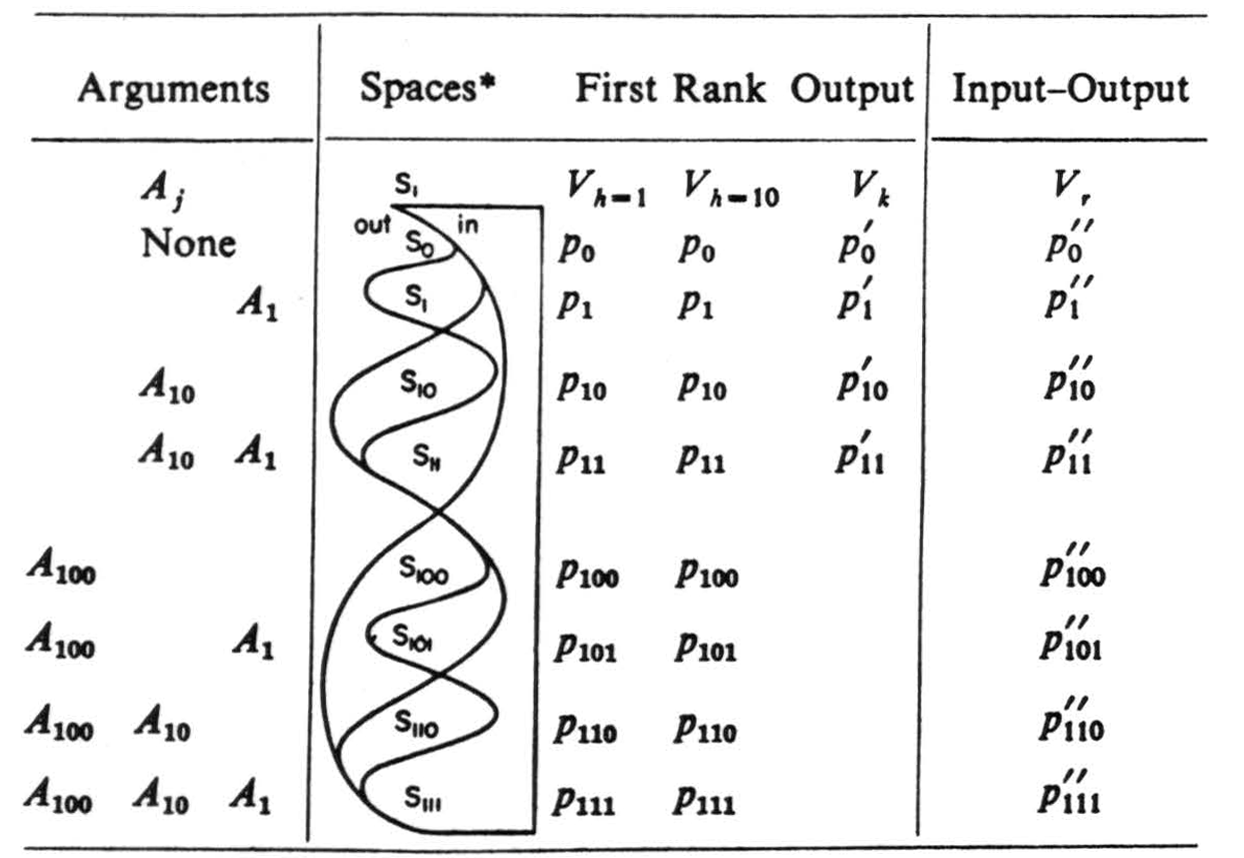
Table 1.

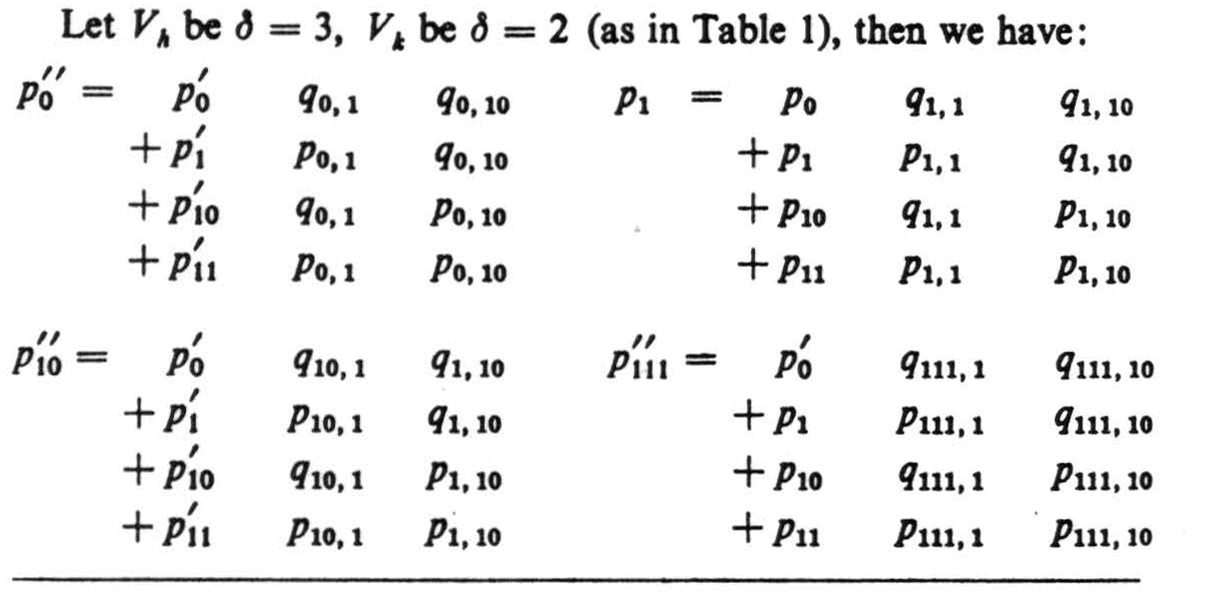
Example 1.

Each i is the sum of one and only one selection of j's and so identifies its space as the concurrence of those arguments ranging from S₀A_j ${S_{{2^{\delta - 1}}}}$ for all of them (cf. column A_j of Table 1). Thus 1 and 100 are in 101 and 10 is not, for which we write 1 ∈ 101 and 100 ∈ 101 and 10 ∉ 101. In the given logical text first replace A_j by V_h with a 1 in S_i if j ∈ i and with a 0 if j ∉ i, which makes V_k the truth-table of A _j with T = 1, F = 0.

Repeated applications of a single rule serve to reduce symbols for probabilistic functions of any δA_j to a single table of probabilities, and similarly any uncertain functions of these, etc. to a single V_r with the same subscripts of S_r as the V_h for the A_j (cf. V_r of Table 1 where q = 1 − p). This rule reads: replace the symbol for a function by V_k in which the k of S_k are again the integers in binary form but refer to the h of V_h, and the p_k of V_k betoken the likelihood of a 1 in S_k. Construct V_r, and insert in S_r, the likelihood p_r of a 1 in S_r computed by equation (1). (See example 1.)

\Pr = \mathop \Sigma \limits_{k = 0}^{k = {k_{\max }}} \,\,{}^{r{'_k}}\mathop \Pi \limits_{h \in k} \,\,{}^{{P_{ih}}}\mathop \Pi \limits_{h \notin k\atop r = i} \,\,(1 - {P_{ih}})\,\,\,\,\,\,\,\,\,\,\,\,\,(1)

Discussion

Uttley: I have thought for a long time about this fascinating theme of reliability out of unreliable units but there is something that is not physiologically clear that worries me very much. Dr. McCulloch started by telling us about the incredible stability and organization of living systems as opposed to desks and chairs and he also said that he once thought a neuron was a bag with salt water inside of it and he now thinks it is highly organized inside.

MCCULLOCH: I certainly do.

UTTLEY: Well, now, I feel that neurons are not crummy, because to suggest that neurons are crummy is rather like suggesting they are filled with salt water. When we first put a microelectrode into some high-level part of the cortex we see apparently random firing impulses. I think it would be very brave to suggest that there is sonic true random principles going on here. We may use the probability theory to sidestep our ignorance, but I am worried about their being real unreliability about. We know in the rods in the retina there is pretty certainly some true randomness arising from the quantum uncertainty. What I rather doubt is that some future Heisenberg will come along and tell us that in the neuron, where we really do know all we can know about it, there is still some uncertainty. So I am very worried about the apparently different attitudes you have about biological systems being incredibly redundant and organized and yet crummy.

MCCULLOCH: Well, let's begin. We are interested primarily in the nervous system. Half of all the people that are in the hospitals of the United States are there because something is wrong in the nervous system; so they constitute a very large fraction of all our woes.

That these things go wrong all too often any psychiatrist can tell you. When you have as your daily customers the man that says that his automobile is twenty-two and twenty-two is his house number and goes to bed in the automobile, you have to realize his circuit doesn't always work correctly. (Laughter.)

Suppose you have to design a circuit to last a lifetime without replacing components. I am 60 years old. In my cerebellum there must be by now at least a 10% loss in the Purkinje-cell population—perhaps a 20% loss. Yet the circuit still works. You have to design a brain so it can get drunk and still find its way home. You have to build it so you can anesthetize it without its dying of respiratory failure. It must take all kinds of abuse, general shifts of threshold, local shifts, etc.

I was amazed when we ran into a 10% variation in the striking voltage at the node of Ranvier, which is probably a fair model of the trigger-point. I had guessed from old measurements of the size of the node of Ranvier that the variation would be less than one-tenth of 1 %, for it seemed larger compared to thermal noise at body temperature. At Teddington, where Dr. Young was in the Chair, I asked him whether I was crazy or whether the measurements were crazy. He said that from electron-microscope studies he believes the effective surface of the node of Ranvier is extremely small.

When we attempt to miniaturize to the extent to which brains are miniaturized, we are going to have trouble at the levels of the component. We have to make use of a redundancy of computation to secure reliability of unreliable components.

That is the crucial thing as far as I can see it. We can pack more and more computing surfaces into the volume but then we have to put these smaller components together so as to build back the stability we would have if we had one large surface.

NEWELL: On the potential command, I was strikingly reminded of the pandemonium model. I wondered if there was some similarity here. And I was also reminded of the high rigidity in all the programming languages that we have to date which are rigid sequential languages. Pandemonium on the other hand is a rule of which it might be said, instead of doing whatever process comes next, you will always do what process shouts loudest. And the principle I thought you were enunciating is the principle that the man who has the information stands up and says, “I know ”—in fact, he is the only one who stands up. We have had one or two other examples of this mostly in the language translation field in which one builds a programming language where one simply salts away in the expression large numbers of programs and then the one with the highest priority says, “I am supposed to work.” He works, and then the next guy says, “I am supposed to work,” and he works.

I think there is a very significant trend in the programming language field to really get new ways of dealing with the language other than sequential controls.

MCCULLOCH: I think it is crucial. I agree with you entirely. I am not sure I caught the totality of the first part of your statement.

NEWELL: It is very like pandemonium.

MCCULLOCH: Yes, it is very like pandemonium in many ways and it will be more like pandemonium when they install it in Jerry Lettvin's artificial neurons. These have the full Hodgkin-Huxley eighth order, nonlinear differential equation to describe their behavior.

Footnotes

References

W. S. McCulloch, Agathe Tyche: of nervous nets—the lucky reckoners Proc. Symp. on Mechanization of Thought Processes, N.P.L., Teddington England.

J. von Neumann, Probabilistic logics and the synthesis of reliable organisms from unreliable components, Automata Studies (ed. by C. E. Shannon and J. McCarthy), Princeton University Press, Princeton, N.J. (1956).

J. von Neumann, Fixed and Random Logical Patterns and the Problem of Reliability, American Psychiatric Association, Atlantic City, 12th May 1955.

J. VENN, Phil. Mag., July 1880.

L. Wittgenstein, Logisch-philosophische Abhandlung, Ann. der Naturphil. (1921).

For further research:

Wordcloud: Afferents, Arguments, Brain, Change, Circuit, Code, Components, Computed, Contradiction, Delta, Diagrams, Equal, Fig, Figure, Fired, Functions, Half, Information, Inputs, Jots, Limits, Logic, Nets, Neurons, Number, Output, Present, Probabilistic, Probably, Psi, Rank, Redundancy, Reliability, Signals, Spaces, Strength, Sum, Suppose, Symbol, Systems, Table, Tautology, Thought, Variation, Venn, Work

Keywords: Systems, Brain-Wise, Physics, Brain, Table, Neurons, Wiring, Logic, Thing

Google Books: http://asclinks.live/a906

Google Scholar: http://asclinks.live/t4z5

Jstor: http://asclinks.live/robi

1 Reprinted from “Self-Organizing Systems” in Self-Organizing Systems, Marshall C. Yovits and Scott Cameron, Eds., Pergamon Press, pp. 264-281, 1960. ↩

2 This work was supported in part of the U.S. Army (Signal Corps), the U.S. Air Force (Office of Scientific Research, Air Research and Development Command), and the U.S. Navy (Office of Naval Research); and in part by the National Institutes of Health. ↩

3 A nondegenerate neuron is a neuron for which a change of one in θ either increases or decreases the number of jots in the Venn symbol by one. ↩

THE RELIABILITY OF BIOLOGICAL SYSTEMS12 [149]