THE STABILITY OF BIOLOGICAL SYSTEMS¹² [140]

W. S. McCulloch

##

There are several kinds of stabilities. There is the inherent stability that comes from making devices out of discrete, disparate parts, so that they either fit and stick or they collapse. It is enjoyed by everything that has a threshold. There are the stabilities based on feedback which are achieved in servo systems. The next kind of stability to consider is one spotted by Ross Ashby and called by him the Principle of Ultrastability; it is based on the possibility of internal switching until the system manages to straighten out its performance, although its responses may have been wrong in the first place.

Still another type of stability is exemplified in the reticular formation in the brainstem. The reticular formation is neither completely orderly nor completely disorderly. If it were either, it would not work. The segments of the human body have their own circuits through the musculature and back again to this same segment of the body. In low forms of life, individual segments can practically maintain themselves. In higher forms, for such a job as walking, agonists and antagonists are not represented entirely in one segment, but are batched into groups of segments.

A segmented animal such as man may be derived from a form in which there was barely a trace of connection between one segment and the next. In the worm, the segments are already joined by short axons in series, so that at the head end, when the distant receptors pick up something, an order can be issued to the worm to shorten itself suddenly. That would not do for man, whose whole mode of organization is different. We not only tie segment to segment, but we also run very fast lines from practically all parts of the body to the core of the brainstem, where lies the net called the reticular formation. From distance receptors, from all of our computers — cortex, cerebellum, basal ganglia — information comes into the reticular formation. Its organization is like a command center to which information comes, variously coded, from all parts of the system and from its own specific receptors. Whenever some part of that reticular formation is in possession of sufficient crucial information, it makes a decision committing the muscles to action. From moment to moment the command undoubtedly passes from point to point in that reticular formation. Let me call the kind of stability obtained in this fashion a redundancy of potential command.

The next kind of stability I am going to discuss was developed in answer to two questions which John von Neumann used to ask. The first is this: “How is it I can drink three glasses of whiskey or three cups of coffee, and I know it’s enough to change the thresholds of my neurons, and I can still think, I can still speak, I can still walk?” The other, equally founded on the consideration of living things, concerns the problem of producing reliable functions, given unreliable elements. This problem is formulated in von Neumann’s lecture, “Toward a Probabilistic Logic.”

I will discuss this kind of stability in terms of computer elements which may be called neurons. They are idealized neurons — over-simplified descriptions of those in our heads. The functions will be used as elements in a kind of substitutive algebra which, to the best of my knowledge, has not been employed heretofore.

Each neuron will be assigned a certain logical function. To visualize the range of possible function, consider a “percipient element” with two inputs, each so simple as to have either one signal or else none on each occasion. For this element, the world is then one of the four cases separated by the arms of the diagonal cross:

Which of the four worlds is the case on a particular occasion will be indicated by the position of a dot:

And let the “percipient element” be a relay which emits either one signal or else none, according to its input, i.e., under none, one, two, three, or all four cases. There are then 16 such “relays”:

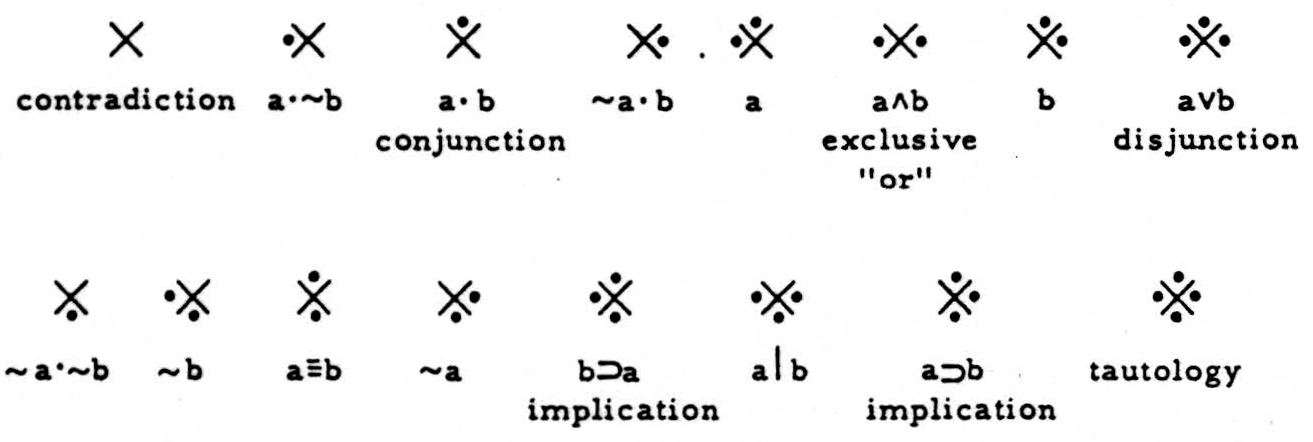
Each computes one logical function, i.e., its output depends upon its input by the one of the 16 logical relations written underneath it. Reading from left to right, the relays in the upper line will fire under the following conditions:

• Never (universal contradiction)
• Signal from A but not from B
• Signal from both A and B (conjunction)
• Signal from B but not from A
• Signal from A (whether or not from B)
• Signal from A or else from B (but not from both)
• Signal from B (whether or not from A)
• Signal from either A or B or both (disjunction)

The relays in the lower line fire if there is:

• Signal from neither A nor B
• No signal from B (whether or not from A)
• Signal from both A and B or from neither (identity)
• No signal in A (whatever from B)
• Signal in B implies signal in A
• Signal in A not more than one input (Sheffer stroke)
• Signal from A implies signal from B
• Under every condition (tautology)

These symbols are exhaustive for the calculus of propositions of the first order.¹

The rule of combination of symbols is simply a substitution of the output of a relay for each of the two inputs;

(X) X (X)

Wherein the ( ) signify that the enclosed X is precomputed from A and B before their outputs reach the unbracketed X. Thus,

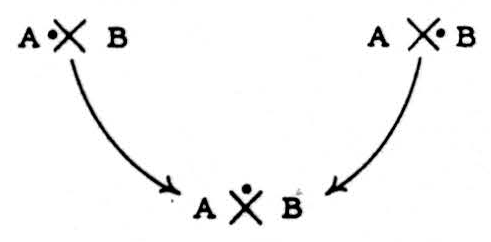
is abbreviated:

so that the parentheses stand for the striking time (or synaptic delay) of the relays, as well as for the serial order of operations.

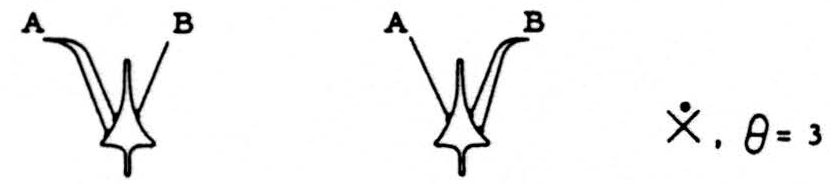
This calculus can be realized by means of conventionalized neurons. It is assumed that these can be excited or inhibited in equal final steps, and that firing or nonfiring depends on whether the algebraic sum of excitations and inhibitions does or does not exceed a given threshold, θ. The following symbols will be used:

With such neurons with thresholds ranging from 4 to −3, and two inputs yielding a total of 3 excitations or inhibitions, we can realize all but two of the 16 logical functions (of course “alphabetical variations” or reversals of right and left are admitted):

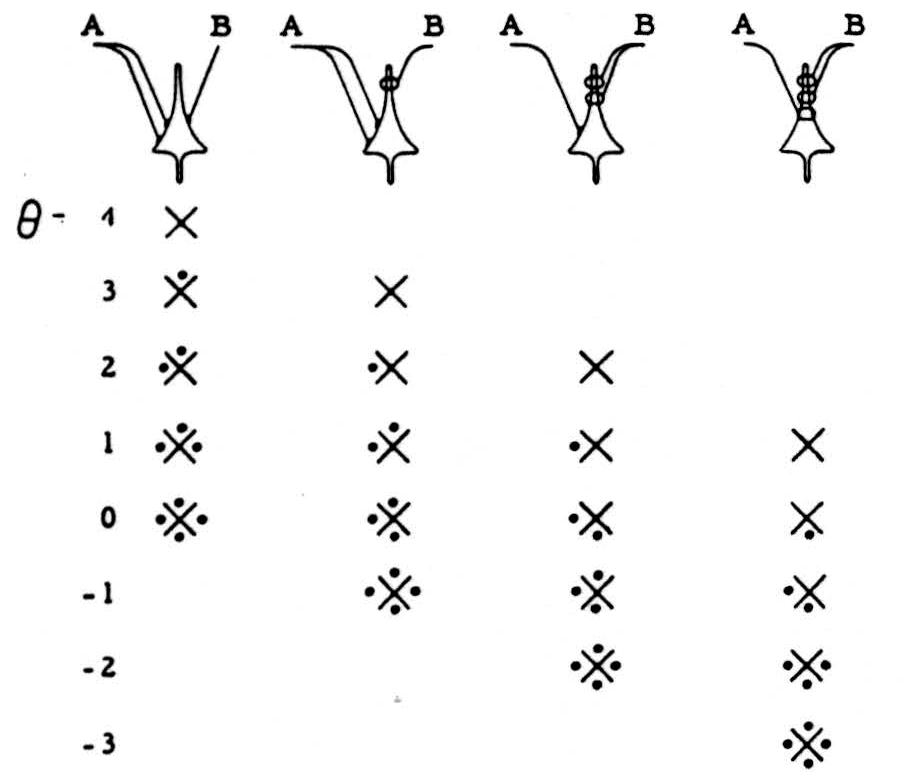
The reason for picking three units of signal is that this number is necessary and sufficient to produce all but two of the logical functions. If the stimuli from A and B are equal in number, then all functions with 2 “dots” (see third sketch) are omitted; but it is still possible to treat those for the kinds of stability here considered, mutatis mutandis.

The missing pair can be constructed by using 3 neurons, but this requires 3 times the number of neurons and an extra synaptic delay. Nature has to compute efficiently in true time, i.e., a minimum number of neurons and minimal delay. Hence one suspects, and finds, interaction of afferent channels. Such interactions of afferents occur, but let us forget them as unnecessary to our argument.

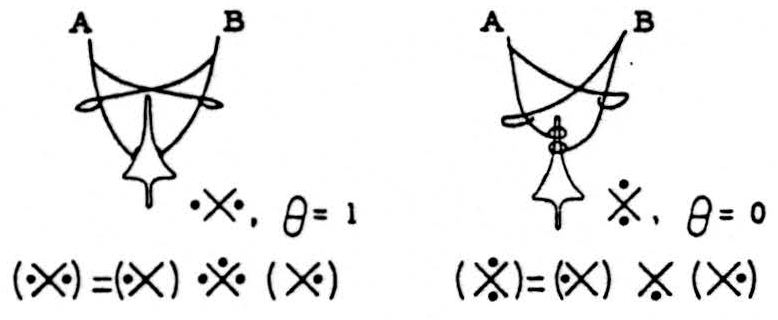
We shall permit the connection of any neuron by either kind of termination to any other neurons. This means that for any but the front-line neurons, the “world” consists of the terminations of two other neurons, each of which, during any given cycle, does or does not fire. With this convention we can construct circuits representing any desired logical functions.

Using only such actions as can be accounted for by impulses reaching and affecting the neuron (or relay), we can invent circuits which will give the same output for the same input, although the threshold of every unit has been shifted in the same direction, so that it is now computing a new logical function; and we can do this for any logical function from input to output. For instance:

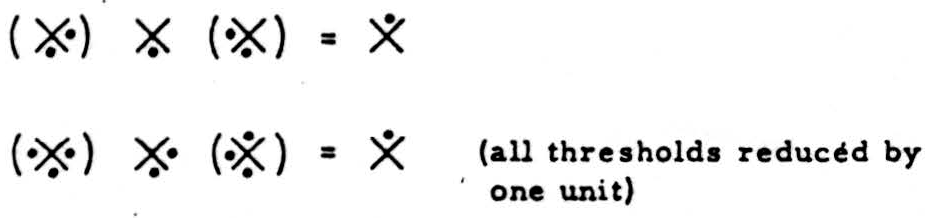
This stability differs in kind from any heretofore described. Let us call it “logical stability.” Its source resides in part in the redundancy of logic itself and in part in the redundancy of the net; for, given 16 types of relays taken 3 at a time, there are 16³ combinations, but all result in only 16 functions — hence the redundancy of the combinations is 16².

The redundancy of logic itself is perhaps best seen in that a relay which should respond only to one input may be in readiness on one-half of all occasions to respond to one other input, and it will be wrong in only one of the 4 cases half the time. For instance:

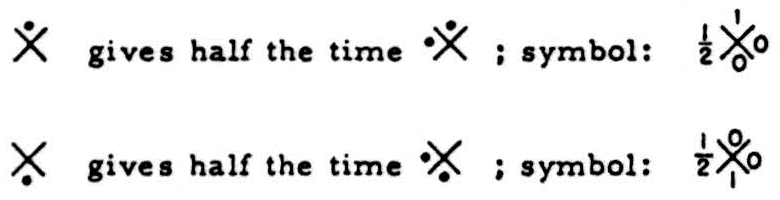
If we dealt with cells having 3 inputs — A, B, C — there would be 8 cases, and the error would occur one in 16 times. In general, if δ is the number of inputs and 1/ρ is the fraction of time when the relay will respond erroneously to one situation, then the fraction of time the relay will give a wrong answer is (l/2^*δ*)(1/ρ). In short, the redundancy of logic of these circuits is of the form (2^2*δ*)^*δ*, in eliminating errors, and we are left with the construction of functions to make use of the best out of 16²⁺¹; combinations for δ = 2. Let us now see how to design circuits for independent variations of threshold.

Consider any combination of three neurons such that the outputs of two form the input of the third. Each of the three “normally” behaves in some given way but occasionally responds when it is not “supposed” to do so, i.e., it errs. Let us suppose the error is either to respond or to fail to respond to a signal from the left (or right). Now this can be harmless in the central neuron if the one on the left (or right) is on this occasion computing the intended function. But if an error at the same instance occurs in that neuron also, the erroneous signal (or erroneous absence of signal) will appear in the output. There is no reason why any erroneous signal in the right (or left) should have anything to do with this performance. For instance, we intend:

but each relay may err some of the time responding to “A” or “A and B” instead of to “A and B”only, these errors occurring with frequencies 1/R, 1/S, and 1/𝒯, respectively, each multiplied, of course, by 1/2^*δ*:

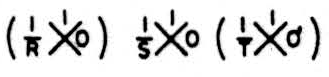
The results are as follows:

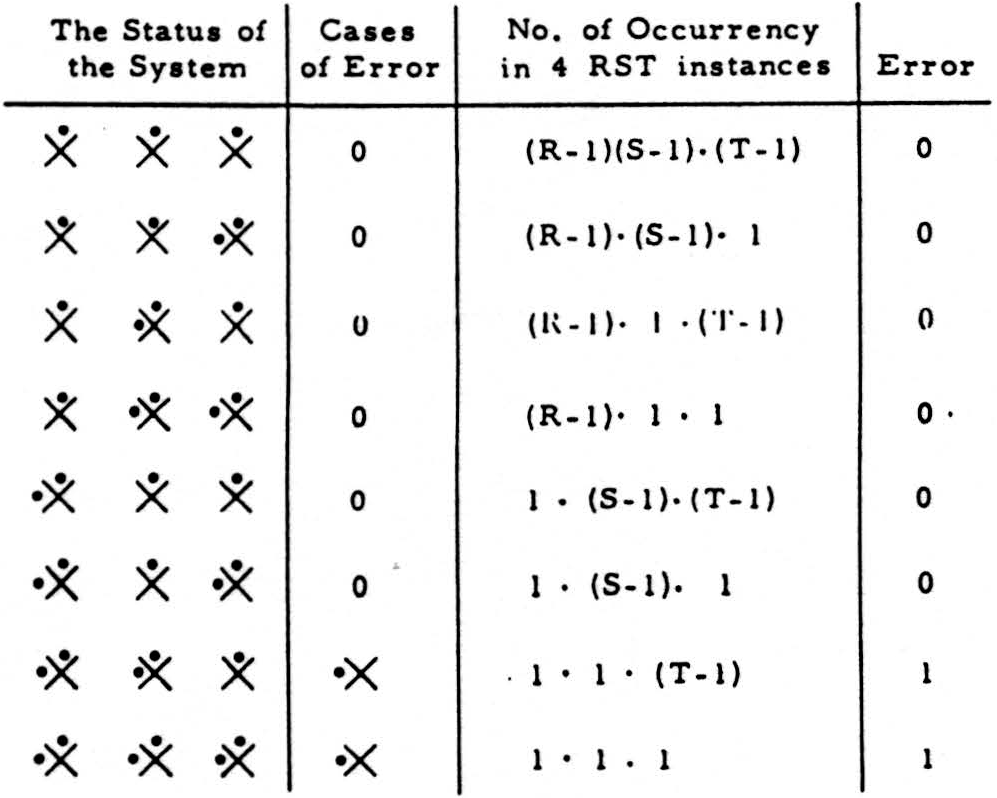
an the error is $\frac{1}{{{2^\delta }}} \cdot \frac{1}{R} \cdot \frac{1}{S}.$

Such a configuration does not enjoy “logical stability” — but for values of R, S, 𝒯>1 it gives a probability of “correct” outputs for inputs better than its components give singly. Compare it with the aforementioned “logically stable” circuit - letting R=S=𝒯 (call their value ρ). The logically stable circuit is error-free for ρ = l, and for ρ=∞.

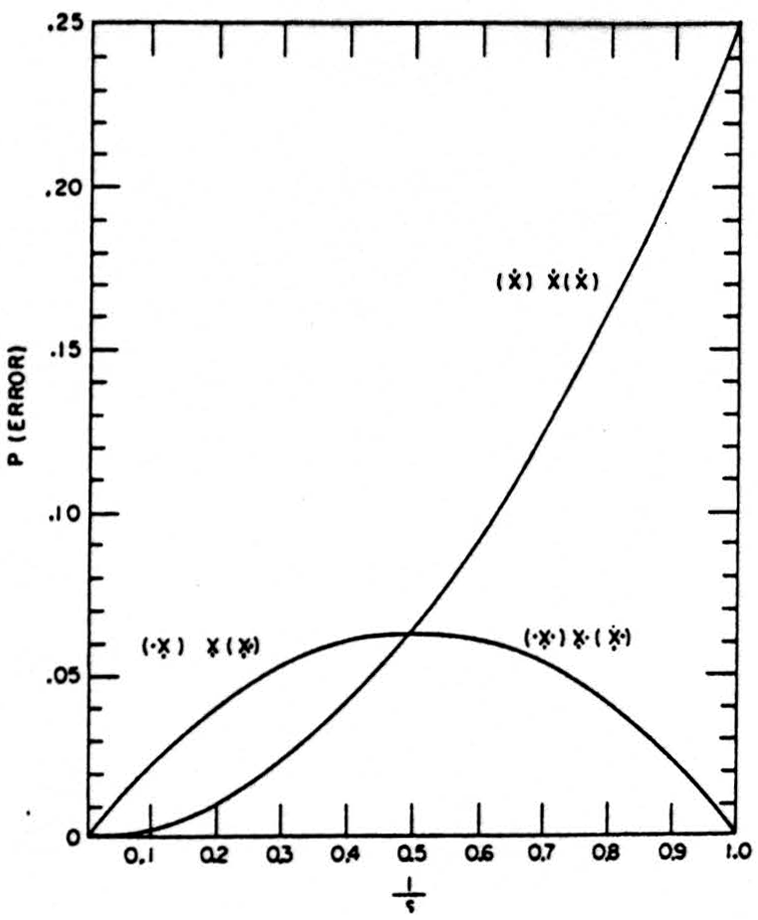
Either type of circuit is useful in constructing a probabilistic logic (i.e., one in which the logical functions themselves are afflicted by random errors) whether the error is attributable to random fluctuations of threshold, signal, or noise of any other origin.

Consider next only those circuits like

wherein the error can enter from one side only. Just as the factor 𝒯 disappeared from the final count of errors, so will any other factor introduced by consideration of functions of more than 2 inputs to each relay. Hence we can write, in general, for such circuits:

No circuits with fewer errors can be devised. We will call such circuits “best.”

Clearly, if best circuits can be so combined as to repeat the improvement at successive stages, one can build a circuit of any desired reliability by going through enough stages. The “trick” is to keep the errors from occurring on both sides simultaneously and thus corrupting the product action of the central, or output, neuron. This can be done, for the function previously considered, by a network composed of neurons of the type

arranged as follows:

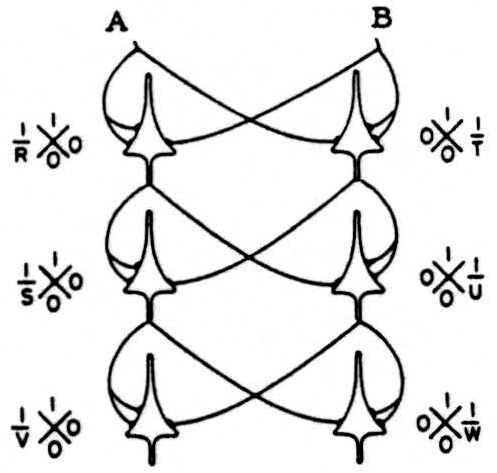
All neurons on the left are going to pass incorrectly a signal from A alone when the threshold is lowered, and all those on the right will err only for a signal from B alone. The error probabilities for the cells in the third rank are 1/4RSV on the left side, 1/4𝒯UW on the right. So, we may write in general that for a net of relays with a width δ = number of common afferents to all neurons, and a depth n of the net in ranks of relays (or neurons), the errors are (l/2^δ)(1/ρⁿ), which requires precisely δ×n−(n−1) = 1+(n−1)δ relays.

The extension to any δ is achieved by substituting “all” for “both” in the center and dealing with a cube of δ dimensions. These functions ran equally well built by using “none” for “neither, nor” in the center. In the constructions using “all,” we put dots in each place in the rank facing the input for the function we desire to compute, whereas in those using “none” we work with the “cube” of all dots less the dots of the function we desire to compute. These remain the “best” constructions for all values of δ and n, provided the value of 1/ρ remains less than that at which it intersects the curve for the best of the logically stable circuits. For values of 1/ρ larger than this, the logically stable are preferable. The best way to combine these nets is still to be found.

I should say, in passing, that I have examined the frequency with which logically stable circuits will occur if connected 2-to-1 but otherwise in random triplets; they constitute about 1/16 of all complexes, and a much larger fraction of all circuits whose output is neither tautology nor contradiction, i.e., of all useful circuits. As for those which improve performance to 1/4ρ², they are at least 1/8 of all triplets with like cells in the first rank, but perhaps there are many more I have not yet found. Of these functions, therefore, the fraction of “best” circuits is not less than (1/16)•(1/8) of all triplets connected at random.

I have examined the circuit in which errors occur in each of the three neurons in three places in this pattern:

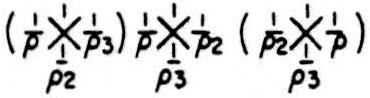
It yields errors with a probability

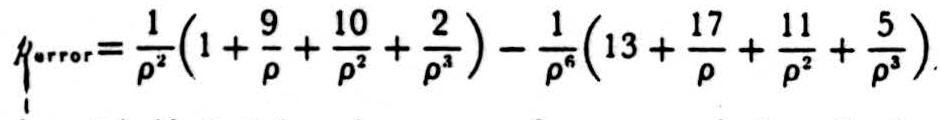
This is less than 1/ρ if ρ⩾4, but the scatter of errors precludes a further diminution by repetitions of the net.

The investigation I have discussed is not finished, but I believe I have demonstrated a method which meets von Neumann’s challenges to find a stability of circuit action under common shift of threshold, and to construct a probabilistic logic with which to secure an increasingly reliable performance from unreliable components.

Footnotes

For further research:

Wordcloud: Action, Best, Cases, Circuits, Combinations, Command, Compute, Consider, Construct, Desire, Dots, Either, Element, Equal, Erroneous, Errors, Figure, Fire, Follows, Form, Formation, Frac, Functions, Give, Given, Input, Instance, Logical, Neither, Net, Neurons, None, Number, Occur, Output, Random, Rank, Redundancy, Relay, Respond, Reticular, Segment, Signal, Stability, Stable, System, Threshold, Type, Used, Values

Keywords: Body, Systems, Circuits, Life, Formation, Segments, Stabilities, Center, Stability, Parts

Google Books: http://asclinks.live/dmxa

Google Scholar: http://asclinks.live/2s4i

Jstor: http://asclinks.live/xa6h