Complex Rhetoric and Simple Games
Jeffrey Goldberg
Cranfield University, ENG
Lívia Markóczy
Cranfield School of Management
Introduction
Disorder, unintended consequences of actions, and turbulence followed by calmer periods are part of the everyday experience of individuals in organizations as a consequence of the many small interactions among individuals and organizations. Organizational scholars have long been fascinated by this dynamism and unpredictability and have sought theories capable of capturing these.
Complexity theory and chaos theory now seem to fill the role. They have been presented in scholarly and practitioner-oriented journals as comprising a revolutionary new paradigm (e.g., Johnston, 1996; McKergow, 1996; Brown and Eisenhardt, 1997) that is not only capable of modeling dynamism and unpredictability, but does so while eliminating the perceived evils in social sciences: reductionism, predictability, and the assumption of rational individuals (e.g., Stacey, 1995; McKergow, 1996). In that discussion, the distinction between complexity theory and chaos theory is often blurred. As we comment on the literature that fails to make the necessary distinction, we will use the term “complexity/chaos theory” as a cover term. We will reserve “complexity theory” or “the study of complex systems” and “chaos” or “chaotic systems” or “nonlinear dynamic systems” for things that more closely resemble the notions as they have come from mathematical physics and modeling.
Complexity/chaos theorists pride themselves in drawing from recent scientific developments in physics, biology, and mathematics. Complexity/chaos theory, however, has also accumulated a rich rhetoric that distorts the picture of what it can do for us. Before we can evaluate complexity/chaos, we need to strip away the rhetoric that surrounds it. Only then can we see how it really contributes.
When we separate chaos from complexity, we will see that most of the actual work in chaos/complexity in management has been with complexity theory (although muddled by some of the rhetoric of chaos) and so we will focus mainly on complexity, but will have something to say about chaos as well.
WHAT PEOPLE SAY COMPLEXITY/CHAOS DOES FOR US
In the management literature, complexity/chaos theory is presented as a theory that, unlike traditional theories, is able to demonstrate how the interaction of agents following simple rules can lead to complicated macroscopic effects in the long run (McKergow, 1996; Levy, 1994).1 The interaction of the agents is said to follow a nonlinear dynamic, and differences in the initial state of a system lead to different interaction patterns among the agents, which lead to unpredictable, often unintended, consequences on the system level (McKergow, 1996; Stacey, 1995). Unforeseen consequences are assumed to be the result of the existence of both negative and positive feedback loops in the system (Cheng and Van de Ven, 1996; Ginsberg et al., 1996). Negative feedback loops by themselves lead to the stabilization of the system, but the positive feedback loops make the system unpredictable and unbalanced as they amplify the effects of certain interactions (Van de Ven and Poole, 1995). Some management scholars consider organizations to be good candidates for the nonlinear dynamic feedback system described by complexity/chaos theory (Brown and Eisenhardt, 1997; Stacey, 1991; Parker and Stacey, 1994). Stacey (1995: 480-81), for example, writes:
Organizations are clearly feedback systems because every time two humans interact with each other the actions of one person have consequences for the other, leading that other to react in ways that have consequences for the first, requiring in turn a response from the first and so on through time. In this way an action taken by a person in one period of time feeds back to determine, in part at least, the next action of that person … Furthermore, the feedback loops that people set up when they interact with each other, when they form network, are nonlinear. This is because: the choices of agents in human systems are based on perceptions which lead to non-proportional over- and under-reaction … and without doubt small changes often escalate into major outcomes. These are all defining features of nonlinear as opposed to linear systems and, therefore, all human systems are nonlinear feedback networks.
Complexity/chaos theory is often presented as superior to existing theories that are concerned with equilibria (McKergow, 1996; Brown and Eisenhardt, 1997). Interest in equilibrium is often equated with “stability, regularity and predictability” (Stacey, 1995: 477), while complexity/chaos theory is claimed to be able to model systems that “operate far from equilibrium” and are at the “paradoxical states of stability and instability, predictability and unpredictability” (Stacey, 1995: 478). Given the occurrence of both positive and negative feedbacks, a complex system might never reach equilibrium.
Complexity/chaos allegedly has a number properties that are claimed to characterize human systems and interactions. Some of these are listed below. These are discussed in more depth later.
- Dynamic feedback Complex/chaotic systems involve dynamic feedback; both positive (reinforcing) and negative (damping).
- Initial state dependence The butterfly effect that small differences in the initial state of a system can lead to very large differences in the final outcome.
- Complex output Many simple interactions between things following simple “rules” can lead to complicated macroscopic effects in the long run.
- Nonlinearity Nonlinear systems lead to unpredictability.
- Antireductionism Complex/chaotic systems are “holistic.”
- Self-reflection This is often (mis)taken as a synonym for dynamic feedback.
- Unstable or no equilibrium Complex/chaotic systems might never reach an equilibrium, which is why they are thought to be highly suitable to model both stability, and instability, predictability and unpredictability.
THE THEORIES
COMPLEXITY VS CHAOS
Chaos and complexity are often discussed together, but are quite different. There are many characterizations of the differences. Cohen and Stewart (1994: 2), for example, claim that complexity is about how simple things arise from complex systems, and chaos is about how complex things arise from simple systems.2 It is generally true to say that the study of chaos generally involves the study of extremely simple nonlinear systems that lead to extremely complicated behavior, and complexity is generally about the (simple) interactions of many things (often repeated) leading to higher level patterns.
To give an example of a nonlinear dynamical system (which we will come back to later), we will look at one famous and simple system. The discussion here is based on Sigmund's (1993) description. This work is also well described by Gleick (1996: 70-73).
PARABLE 1 Imagine a simple species whose population in one generation depends only on its population in the previous generation in two ways. If there are more potential parents there will be more offspring in the next generation, but if there are too many in one generation they each may not get enough nourishment to reproduce. Also to make things simple, let's set the units that we use for talking about the population so that 1 is the absolute maximum that the particular environment can hold. So, in the ith generation the population xxi depends on the population of the preceding generation xi-1 according to some equation. Probably the simplest function that fits the description is an inverted parabola
xi = kxi-1(1 - xi-1)
where k is some constant. That equation is very simple, but it is nonlinear (when multiplied out it is xi = kxi-1-kx2i-1). For some values of k, most starting values for the population, x0, will eventually lead to a single point (depending on k and not on x0). For other values of k, most starting values for the the population will lead to oscillating or cyclical values for the population (and the cycles can be quite long). But for other values of k, starting values for x0 don't necessarily converge on any repeating cycle and the population fluctuates in a way that is neither cyclical nor random. When this happens, no difference in starting x is so small that it might not make a big difference when a system behaves that way it is chaotic.
Chaos theory as used in biology, physics, and mathematics is about how to recognize, describe, and make meaningful predictions from systems that exhibit that property.
Complexity theory (or the study of complex systems) is really about how a system that is complicated (usually by having many interactions) can lead to surprising patterns when the system is looked at as a whole.
For example, each of the billions of water molecules does its own thing when it joins up with others as it freezes to others, given some constraints on what each of them can do, and something recognizably snowflake shaped can emerge. Complexity theory is about how the interaction of billions of individual entities can lead to something that appears designed or displaying an overall systems-level pattern.
There is actually a relation between complexity and chaos that we have been ignoring, but an actual relation is something we have not seen mentioned in the management literature. Some complex systems with entirely linear interactions between agents can be approximated at the macroscopic level with nonlinear relations. However, the fact that some systems have such a relationship doesn't mean that they all do. The relationship must be justified in each and every case.3
GAME THEORY
There are some excellent introductions to game theory suitable for students of management (e.g., Dixit and Nalebuff, 1991; Gibbons, 1992; McMillan, 1992), as well as others that are better suited to those with some undergraduate training in economics (e.g., Binmore, 1982; Kreps, 1990); there are also shorter introductions, designed for economists, that can help provide an introduction (e.g., Gibbons, 1997). Those are all excellent sources for developing an understanding of game theory.
One difficulty we face here is overcoming some management scholars' preconceptions of game theory. We have seen more than a couple of (unpublished) manuscripts that equated all of game theory with one very particular game, the Prisoner's Dilemma. Game theory is far broader. Basically, there are two kinds of decision (or action) situations involving several agents or decision makers. A situation is parametric if the decisions of the agents are independent of each other (although the outcomes may be an effect of interaction), while a situation is strategic if the actions or decisions of the agents depend on each other. In a perfect market, setting the price for a product is a parametric decision because no single individual decision can affect the overall market. In a duopoly, price setting is a strategic decision. Game theory is about strategic decision making in this sense. Dixit and Nalebuff (1991) provide a series of cases where game theoretic, or strategic, thinking is important.
A rough typology of games that game theorists talk about is as follows:
- Static games with complete information (e.g., one-shot Prisoner's Dilemma, Chicken) These are games where all of the decisions to be made by all of the players are made simultaneously. However, because players can think about what the other players will think about what they will do, these do—despite the name—involve a certain amount of feedback and self-reflection.
- Dynamic games with complete information (e.g., repeated Prisoner's Dilemma, Ultimatum Game) In these games, players take turns.
- Static games with incomplete or asymmetric information These are just like the static games, except that not all players have full knowledge of the parameters of the games, or they have limited (bounded) rationality.
- Dynamic games with incomplete information (e.g, “auctions” and “signaling games”) These are just like the dynamic games except that not all players have full knowledge of the parameters of the games or they have limited (bounded) rationality.
For all of the above there are both cooperative and noncooperative games leading to a typology of eight types of games. Additionally, all of these types can include two-player games, two-player games, or games involving any finite number of players. When we talk about game theory in general, we mean to include the theory that describes all of these types of games, and not just the two-person static games with complete information that are so often used in examples for simplicity.
There is a special kind of game theory, evolutionary game theory, which is largely indistinguishable from much of the better work done under the name of complexity. Sigmund (1993) provides a very accessible introduction to some of the concepts of evolutionary game theory (as well as discussing complexity and chaos). Schelling (1978) provides an enjoyable and accessible discussion of some game theoretic problems and solutions that have a very strong “emergent properties” feel to them.
More interestingly, there is also what has become known as behavioral game theory, which is described in an outstanding review of the topic by Camerer (1997). Behavioral game theory takes as its agents real humans with their sense of fairness, cognitive limitations, and decision biases. Some of our recent work on understanding cooperation has been in this area (e.g., Goldberg and Markóczy, 1997).
THE COMPARISON GAME
We can most effectively discuss the particular properties attributed to chaos/complexity— and in doing so clarify and demystify them as well as evaluate their desirability and novelty—by making a comparison with game theory.
SIMILARITIES
Dynamics and feedback
Probably one of the most attractive features of complexity/chaos theory is that it uses a system of dynamic feedback (e.g., Cheng and Van de Ven, 1996; Ginsberg et al., 1996; Van de Ven and Poole, 1995). The value of some variables at any given time is (partially) a function of the values of the same variables at an earlier time. How an organization works today is a function of (among other things) how it worked yesterday.
Game theory may at first appear to lack this dynamism because static games don't involve time. Yet even in static games, game theory, through its recursive awareness, incorporates dynamics. A typical game might first involve reasoning of the form: “I know that she knows that he knows that I know that she knows…” Game theory explicitly provides the tools for managing such a loop and determining (for many cases) what decisions the infinite expansion of such a loop would yield. The self-reflection of even static games gives them a dynamism and a feedback all their own.4
The dynamism and feedback of chaos/complexity require iterations over time, and they are often based on trial and error. Sometimes it is the dynamism of the game theoretic type that matters, where trial and error is just too slow or ruled out for other reasons. We provide a somewhat extreme (and grossly simplified) example. See Kavka (1987: Chapter 8) and especially Schelling (1980: Part IV) for discussions that are not so grossly simplified.
PARABLE 2 Roughly speaking, the strategic policy during much of the Cold War between the US and the USSR was based on Mutually Assured Destruction (MAD). If a war were to start, both participants would be devastated. Although there would be an advantage to whoever started first, neither side would have “first strike capability.” This made it in the interest of both parties to avoid a war.
Suppose, however, that one side started to develop technology that might make it able to survive such a nuclear exchange (e.g., President Reagan's “Star Wars” proposal). Once a working missile defense system is in place, there is no longer Mutually Assured Destruction. The US might then have first strike capability. When one side has first strike capability, it is in its interest to strike first. It has a strong incentive to strike before the other develops first strike capability in its turn. It is also in the interest of the side without first strike capability to strike first, since by doing so it can at least reduce the damage if would suffer if the other struck first. Both know this about each other, and so both know that the other knows that they know that it is best to strike first; so the first strike is bound to come soon, so push the button now!
This is not a very healthy situation. And it gets even worse. If one side is developing first strike capability, it is in the interest of the other to strike before the missile defense system is deployed. Naturally, since the first side knows this… Furthermore, it doesn't even matter if the defense system isn't technologically feasible. If at least one side believes that the other believes that it believes that it might be feasible, then it is in the interest of both sides to strike first.
What can be done to prevent such an unstable and dangerous situation? The answer is the Antiballistic Missile (ABM) treaty of 1972 (and its predecessors). The ABM treaty paradoxically—but correctly—placed no limit on offensive missiles, but strictly limited the deployment of missile defense systems (and then only to missile bases) to ensure that no side would have first strike capability.5
The ABM treaty did not evolve out of many iterations of generations of learning what strategy works best. It had to work the first time (and thankfully it did). The paradoxical treaty that might have saved the world required thinking about feedback loops, and it required thinking about thinking. That is, it involved both feedback and self-reflection. While selfaware actors are able to reach solutions the first time just by thinking about feedback loops, most complexity models require many iterations before the shape of any equilibrium becomes clear.
Even with nominally static games, there can be a sense of dynamism. Game theory also explicitly incorporates dynamic games that include repetitions or turn taking. While we have illustrated a similarity (feedback and dynamics), we have also highlighted a difference (self-reflection), to which we will return later.
Initial state dependence
Many people find an attraction in complexity/chaos theory that it allows very small differences in the initial conditions to lead to very large differences in later outcome (e.g., Johnston, 1996; McKergow, 1996). This, they argue, helps us explain the unpredictability of aggregate outcomes from the interactions among individuals or organizations. The above is often called the butterfly effect. A butterfly flapping a wing in Brazil can be the difference that means there is a blizzard two weeks later in New York. McKergow (1996: 722) describes this effect:
There are some attributes which are associated with complex systems. Such systems are self-referential … They are non-linear, so that a small change can lead to much larger effects in other parts of the system and at other times.
People often associate this feature of complexity/chaos theory with its reliance on nonlinear models and do not consider alternative theories that rely on linear models (e.g., Johnston, 1996; McKergow, 1996). Nonlinearity, however, is neither necessary nor sufficient for one kind of butterfly effect.
An article in The Economist (1998) on public misunderstanding of science mentions the butterfly effect:
Reading a book rich with subtle and unfamiliar ideas is a bit like having a custard pie thrown at you: the few bits that stick may not resemble the original very closely. James Gleick's book Chaos was clear and well-told, yet many readers came away with little more than the notion that a butterfly flapping its wings in Miami can cause a storm months later in New York. (Economist, 1998: 129)
The often discussed cases of standards battles6 provide a good example of perfectly linear and simple systems leading to butterfly effects.
PARABLE 3 Imagine a world with two kinds of people, those who produce keyboards and those who type or learn how to type. Let's suppose that a producer of keyboards can produce a “qwerty” keyboard arrangement or a “dvorak” keyboard arrangement. Let's also suppose that all other things being equal, the dvorak arrangement is better for typing.7 It is in the typist's interest to learn the system to which most keyboards will be produced, and it is in the manufacturer's interest to produce the kind of keyboard that most people use.
This is a situation with two stable evolutionary equilibria. In one everyone is using or producing dvorak keyboards, and in the other everyone is using or producing qwerty keyboards. If everybody had perfect information and started from a position where there was no prior commitment to either of the two types, all would choose to use and produce dvorak keyboards. However, if there are initially a few consumers who prefer qwerty or manufacturers who overestimate the number of people who prefer qwerty, the less optimal qwerty equilibrium may be reached instead.
In fact, very small differences in the numbers of initial consumers preferring qwerty (or just in the estimate of these numbers from some of the manufacturers) can lead to one equilibrium being reached instead of the other. Depending on the initial conditions and the amount of imperfection of knowledge in the system, something as small as a butterfly's wing could tip the balance one way or another.
The basic model has only to list people with their preferences. Those preferences can be on a linear, or even ordinal scale. Yet still a small difference in the initial conditions can lead to large differences in the final state. So nonlinearity is not a necessary condition for the butterfly effect.
Another example might be a somewhat simplified pool table that can be modeled with linear relations only. Yet small differences in a shot can lead to winning the game or losing.
If we return to the nonlinear dynamical population model discussed earlier, xi = kx*i*-1 (1 - x*i*-1), we will find that for some values of k, the initial population, x0, has no effect on the final outcome. For example, if k = 3.2, the population will end up alternating between 0.513 and 0.799 no matter what x0 was initially picked. This goes to show that nonlinear dynamic feedback is not a sufficient condition for the butterfly effect.
The lesson here is that nonlinear dynamics is neither necessary nor sufficient for the small initial differences leading to large differences in output. However, it is commonly thought to be necessary, and it is not accidental that people believe in a special relationship between chaos and the butterfly effect. That is because there is a very peculiar and fascinating type of butterfly effect that is unique to some parts of some nonlinear dynamical systems. If we return to that population model, we can illustrate the special, or chaotic type of butterfly effect. If we set k = 4.0, then the initial values for x0 matter greatly. Not only will small differences in x0 lead to different results, but there is no difference so small that it won't make a difference. But remember that not all nonlinear dynamical systems behave in this way, and those that do, only do so for certain ranges of initial conditions.
The stranger kind of butterfly effect is interesting in its own right, but we do not see that it says anything about the sorts of models that management scholars should or shouldn't be exploring. Since our ability to measure initial conditions is so limited, it hardly matters which sort of butterfly effect is in place. But if we keep our models linear, we can more easily use them to examine what does occur.
Predictability
It appears that some people are attracted to the notion of the weird sort of butterfly effect because they think that it rules out predictions (e.g., McKergow, 1996; Johnston, 1996). Fortunately, they are wrong.
PARABLE 4 The earth, the moon and the sun form a nonlinear dynamical system in exactly the way that leads to the weird sort of butterfly effect. No matter how precisely we measured the mass and velocities of the earth, moon, and sun (short of truly perfect measures, which are impossible), we could not predict their ultimate positions in the far future. We are not able to say when moonrise will be in London one million years from today. But we still can predict quite accurately when it will be a few years from today based on today's measures.
The unpredictability that is inherent in some nonlinear dynamic models may take time to settle in. One cannot simply declare a model useless for predication without making some calculation of how long it takes it to diverge. Predictions of moonrise, tides, and the weather all rely on nonlinear dynamical models, and they do get it right most of the time.8
Furthermore, even the behavior of a system that becomes chaotic very quickly is “constrained” in a way that does allow for some interesting and useful predictions. Chaos theory allows us to make predictions about systems that may at first appear random, but can, in fact, be described by simple models.
Determinism
Along with unpredictability, many of those looking at complexity/chaos (and particularly chaos) claim that these systems are nondeterministic. Usually that claim is bolstered by pointing out the butterfly effect and problems of predictability. Chaos does have something interesting to say about determinism, but it is quite the opposite of how some people have taken it. Chaotic systems are deterministic. If we go back to May's example in Parable 1, the equation is entirely deterministic. The state of the system at one stage is completely and entirely determined by the state at a previous time. These are deterministic systems, based on deterministic equations. What is interesting about chaos is that it shows how apparently random behavior can be described by completely deterministic systems. One of the founding papers in the chaos literature is entitled “Deterministic nonperiodic flow” (Lorenz, 1963). Gleick's account of that work includes:
His colleagues were astonished that Lorenz had mimicked both aperiodicity and sensitive dependence on initial conditions in his toy version of the weather: twelve equations, calculated over and over again with ruthless mechanical efficiency. How could such richness, such unpredictability— such chaos—arise from a simple deterministic system? (Gleick, 1996: 23)
The FAQ (list of answers to “frequently asked questions”) for the internet newsgroup news:sci.nonlinear also makes it clear that these systems are deterministic:
Dynamical systems are “deterministic” if there is a unique consequent to every state, and “stochastic” or “random” if there is more than one consequent chosen from some probability distribution (the “perfect” coin toss has two consequents with equal probability for each initial state). Most of nonlinear science—and everything in this FAQ—deals with deterministic systems. (Meiss, 1998: §2.9)
A very useful essay on chaos and complexity for management also correctly points this out:
Chaos theory models are deterministic and simple, usually involving fewer than five evolution equations … That is, system behavior can be described using few equations that include no stochastic inputs. These two features highlight one of the least intuitive aspects of chaos theory: complex … outcomes can be generated using very simple deterministic equations. (Johnson and Burton, 1994: 321)
What attracts attention is not that these systems aren't deterministic (they are), but instead that these deterministic systems behave in ways that superficially resemble some nondeterministic systems.
If everything there is to know is known about the initial state of a system, then it is in principle possible to predict later states with perfect precision, assuming perfect computation. But it is not possible to know everything there is to know about a system, nor is it practical to compute things with perfect precision. These practical limits on determinism have been known for centuries, and are not new discoveries at all.9
Complex output
One of the appeals of the complexity approach is its ability to generate surprising (or at least nontrivial) macroscopic effects from the iterated interactions of many microscopic agents (Brown and Eisenhardt, 1997). Often complex structures (from which the approach derives its name) are visible at the macro level. These structures appear to emerge from the lower-level interactions.
This emergent complexity is fascinating. But is it new or unique to the new paradigm of complexity? No, it is old hat. In the natural sciences, the laws of gases, black body radiation, the shapes of galaxies are all old examples. Economists have been looking at exactly these sorts of emergent phenomena. Game theorists have delighted in showing how some very simple games can lead to very complex-looking behavior. Game theorist Schelling (1978) has a delightful book that lists many such examples, from the way that an auditorium can fill up to the pattern of people switching on headlights as it gets darker.
Equilibria
Some claim that game theory and complexity theory deal with equilibria in very different ways:
Even the most complex game theoretic models, however, are only considered useful if they predict an equilibrium outcome. By contrast, chaotic systems do not reach a stable equilibrium; indeed they can never pass through the same exact state more than once. (Levy, 1994: 170)
But contrary to popular belief, game theory, complexity theory, and chaos theory say more or less the same about equilibria. There are some differences, but those differences don't matter a great deal in light of the similarities. First, however, it is crucial to clarify a few concepts.
An equilibrium can have any degree of stability. Some equilibria are very unstable (see Figure 1a), others can be very stable (Figure 1b), while yet others can be moderately unstable (Figure 1c). A very small amount of noise or turbulence can take a system out of an unstable equilibrium; only a large disruption or shock will take a system out of a very stable equilibrium, and a moderate disruption can take a system out of a moderately stable equilibrium. What is important to note here is that all of the theories under consideration share this. Some games can have moderately stable equilibria; some complex systems can have moderately stable equilibria; some nonlinear dynamic systems can have moderately stable equilibria.
Another point in which the perspectives don't disagree is that all allow for multiple equilibria. Some games will have multiple equilibria; some complex systems will have multiple equilibria; some nonlinear dynamic systems will have multiple equilibria. These multiple equilibria will each have their own degree of stability. The tender trap discussed above has three equilibria, two of which are evolutionarily stable (Figure 1d).
A third point of agreement is that each of these theories allow for systems that have no equilibrium. While it is true that the simplest kinds of games (two-player complete information static games) are guaranteed to have at least one equilibrium, that does not always hold of other types of games (e.g., the “Dollar auction” has no equilibrium; Poundstone, 1992). Moreover, even for these simplest types of games, the equilibrium might involve a “mixed strategy” that behaves probabilistically (e.g., with a rule like “pick action A with 70 percent probability”).
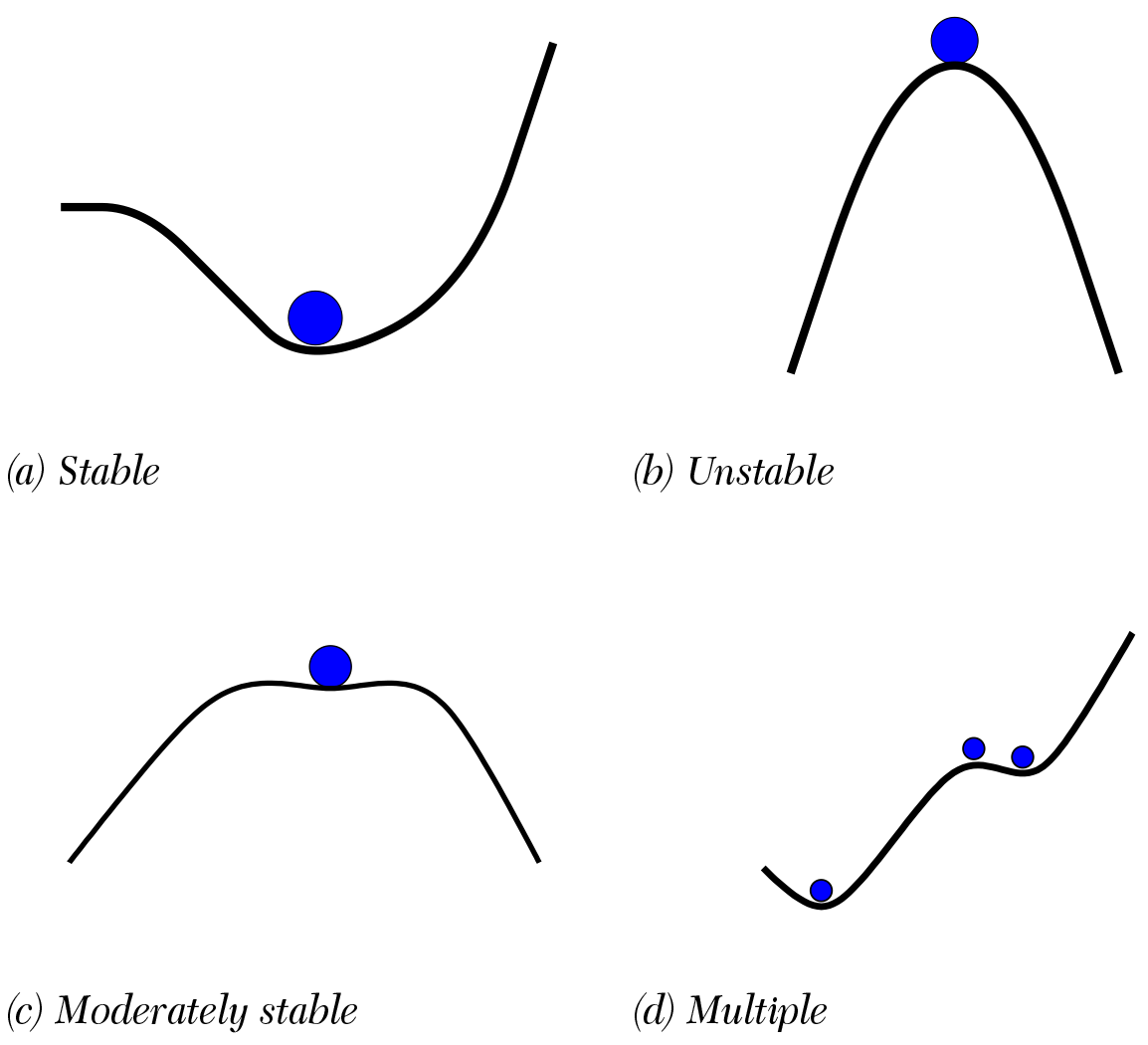
Figure 1. Types of static equilibria
A fourth similarity is that all of these views accommodate dynamic equilibria. A system can be in a cyclical equilibrium if it goes from, say, state si to state sj and eventually back to si. So if it ever gets into one of the states in that cycle it will cycle around forever if the equilibrium is sufficiently stable.
Nonlinear dynamic systems can, uniquely, have a type of equilibrium called a strange attractor, which resembles a cyclical equilibrium with the important exception that the system doesn't actually ever repeat itself. As the system goes from state to state it stays (depending on how stable the attractor is) within a set of possible states. So, while a particular path or state is unpredictable, the set of states to which the system can go is not arbitrary and can be predicted.10 In addition to the strange attractor, which is unique to nonlinear dynamical systems, there are two differences in the ways that equilibria are dealt with. The first difference is that most of the people who are involved with game theory think that it is worthwhile to calculate the equilibria of a system and show how stable those equilibria are if they exist; many people involved in complexity theory think that it is not worthwhile to calculate the equilibria, but instead that it is best to run computer simulations until the system arrives at a reasonably stable equilibrium. Note that this is not an actual difference in the theories, but a difference in the people who use them. One can take identical models and either calculate the equilibria or run simulations or both.
There are some advantages to both methods. In calculating equilibria, if it is done correctly, one knows that all of them have been found, while with the computer simulation, you only know that one reasonably stable one has been found, but may miss others.11 Additionally, other properties of the equilibria can be made clearer through a game theoretic analysis that may not be available through a simulation. The advantage of a simulation is that it is easier. Sometimes the model is so complicated that it is extremely difficult to do anything else; at other times it can be an aid to the calculation, since the simulation can often tell us what one equilibrium is.
Robert Axelrod, an important and clear-thinking developer of complexity, describes complexity simulations (“agent-based modeling” in his terms) extremely modestly:
Agent-based modeling is a third way of doing science. Like deduction, it starts with a set of explicit assumptions. But unlike deduction, it does not prove theorems. Instead, an agent-based model generates simulated data that can be analyzed inductively. Unlike typical induction, however, the simulated data come from a rigorously specified set of rules rather than direct measurement of the real world. Whereas the purpose of induction is to find patterns in data and that of deduction is to find consequences of assumptions, the purpose of agent-based modeling is to aid intuition. (Axelrod, 1997: 4-5)
Axelrod may be being a bit too hard on the approach he is advocating, in that if he is correct it abandons the best of deduction (theorem proving) and the best of induction (inference from the real world) and combines what remains in a technique for aiding intuition. However, the use of explicit models is what makes this approach more valuable then many other means of aiding intuition.12
Returning to the one new factor in complexity/chaos with regard to equilibria—strange attractors—we have yet to see how this particular entity is useful for the study of social sciences, however.
Path dependence: You can't get there from here
Any one of the types of systems might have several (or no) equilibria. Some equilibria might be stable, but without there being a path from some particular state to that equilibrium. This property is not unique to chaos/complexity, but arises in some of the relatively simple games discussed by game theorists. The tender trap with partial information is one of these. Once you get stuck with one standard, it is difficult to move to a more desirable equilibrium because the intermediate steps are unavailable (see also Figure 1d). So, again, complexity/chaos offers us nothing new here, except that it may have served to introduce people to these concepts if they were unfamiliar with them.
DIFFERENCES
Linearity
As we have suggested above, the attractiveness of nonlinearity seems to be the desire to produce models that exhibit the butterfly effect. We have already argued that nonlinearity is neither necessary nor sufficient to achieve the simple form of this effect. Furthermore, it is not enough to show that nonlinearity exists in the world to add it to a model; this complication must be individually and specifically motivated. Its proponents must show that it is necessary to get a useful model. People promoting something that makes models so much harder to handle need to do two things:
- They need to provide good theoretical reasons for the basic nonlinear equations they wish to add. Plausibility arguments for those equations are not enough if one can also provide a plausibility argument for a linear alternative.
- They must show that after their modification from linear to nonlinear they can achieve some solid result that would not otherwise be available.
We don't feel that even the first of these has been done for the case of nonlinearity in the social sciences, much less the second. The situation has not changed since Elster (1989: 3) made this point:
I am not sure, however, that [nonlinearity] is the right direction in which to look for sources of unpredictability [in the social sciences]. The nonlinear difference or differential equations that generate chaos rarely have good microfoundational credentials. The fact that the analyst's model implies a chaotic regime is of little interest if there are no prior theoretical reasons to believe in the model in the first place. If, in addition, one implication of the theory is that it cannot be econometrically tested there are no posterior reasons to take it seriously either.
To our knowledge, there have only been two arguments in the management literature for introducing nonlinear equations into models. One is that nonlinear dynamic systems involve both positive and negative feedback loops (e.g., Cheng and Van de Ven, 1996; McKergow, 1996). People correctly want models with feedback loops and seem to think that if there are feedback loops there must be a nonlinear dynamical system. In some unpublished manuscripts we have seen, authors have explicitly insisted on nonlinearity for the sake of feedback loops, and yet gone on to work with models that are entirely linear.
The other reason that is given to motivate nonlinearity is unpredictability (McKergow, 1996). We have argued that nonlinearity is neither necessary nor sufficient for unpredictability. Even if it were, it could only be used as a motivation for the existence, somewhere in the interactions, of nonlinearity. It cannot be used to motivate a particular nonlinear interaction that must be either theoretically or empirically motivated.
The better studies (Richards, 1990; Cheng and Van de Ven, 1996), which actually looked for and found the very specific sort of unpredictability that comes with some parts of some nonlinear dynamical systems, did so by filtering out every linear relationship available from the data. Once all linearity was filtered out, all that could remain were true randomness and nonlinear variation. The researchers found that there was a nonrandom nonlinear-type component to the variation. But it must be recalled that this was done after filtering out all linearity. If you filter out everything except for what you are looking for, then no matter how small the object of your search turns out to be you will find it. Furthermore, we have no reason to believe that the nonlinearity is a fact about the system under observation. Like the randomness, it could have been introduced at any stage in the process from data collection onward. These are interesting studies, but until some difficult follow-up work is done, the best that can be concluded is that some of the apparent randomness in the data analyzed may be the result of simple interactions. A prior “critique” of the approach used by these better studies is given by Johnson and Burton (1994), and readers are referred there for discussion of the applicability of chaos to the study of management in those cases where the chaos theory is used with understanding.
Self-reflexivity
In the standard complexity examples that have been used, agents are simple-minded entities that follow simple-minded rules. In game theory, agents can anticipate the future and the consequences of their actions and the actions of others. To ignore the ability to reflect may be ignoring exactly the sorts of factors that make human systems interesting. Systems without the ability to reflect or anticipate may be extremely interesting, for after all evolution cannot look to the future. However, evolution can build agents that do look into the future. When we talk about human systems, it seems reasonable to leave open the possibility, as game theory does, that the agents think about their situation and what they are doing.
Game theory, like complexity theory, works on the interactions between fairly simple and abstract agents. The core ontologies of both theories are very simple. In fact, the only real difference in the ontologies of the theories is that in game theory agents can make conscious decisions aware, to some extent, of their own predicament and that of others.
Is it important to consider the reasoning of self and others in interaction when trying to model system with many interactions?
PARABLE 5 Suppose that you and someone else (let's call her Alice) are to meet at 12 noon on a particular day on Manhattan Island, but you forgot to arrange a meeting place. Neither of you lives there or has an office on the island. Neither of you carries a mobile phone. Where would you go?
Before reading what studies show the most common answer to be, you should stop and think about the options yourself. Write down an ordered list of locations.
In a series of studies of questions like this (Schelling, 1980), it appears that the overwhelming first choice is Grand Central Station. While an impressive piece of architecture, it is not really many people's favorite place to wait for other people. Very few of us would actually arrange to meet someone there, but it is where we would go when the meeting place wasn't arranged. When you thought about this problem, you must have thought about what Alice would think about what you thought. That is reflection on others reflecting on your own state of mind.
By self-reflection, humans are able to exclude early on some highly unlikely options from their decisions and substantially reduce the number of possible outcomes. But the agents described by complexity/chaos theory would just move all around New York and the chance that they would meet be very small indeed. Self-reflection and reflection on others clearly play an important role in this example, reducing the set of possible outcomes by excluding highly unlikely options.
Some might argue, however, that although in certain situations selfreflection might be necessary, most organizational activities are routine and do not require self-awareness and foresight. Some people might feel that they are “just a cog in a wheel of a big machine,” but even that makes them profoundly different from a cog in a wheel of a big machine. Real cogs in real wheels never think of themselves as such.
Even where an organization is designed to minimize its members' understanding of it, people will try to figure out what their place is, as the following example suggests.
PARABLE 6 Bletchley Park (BP) was the site of UK code-breaking activities during the Second World War. At various times it employed more than 12,000 people. The code breaking (and particularly its substantial successes) had to be kept strictly secret. To a very large extent, BP was an information-processing center. Some of the steps in processing the information involved people, and some involved machines. It seems that here is the perfect setting to have people act as mindless agents playing their small part and not thinking about the whole picture or even where they fit in.
While this may have been more true of BP than of any other organization, it appears that it didn't work that way. Reports from people who worked there indicate that while they were not really supposed to know what was going on outside of their own narrow activities, they did have a sense of what was going on. In fact, it appears that in order to maintain commitment, people were even deliberately shown where their work fitted in. The operators of the Turing bombes performed “soul-destroying but vital work on the monster deciphering machines” (Payne, 1993: 132) used in some steps of Enigma decoding. The operators were specifically taken to the British Tabulating Machine Company at Letchworth “to watch [the machines] being made and to encourage the workers, although we thought their conditions were better than ours. It was a surprise to see the large number of machines in production” (Payne, 1993: 135). Apparently it was felt that various people needed to see other bits of the operation (or at least some of the other people involved) to be encouraged. Also for the operators to have been surprised by the number of machines being built, they must have had a sense (even if incorrect) of the scale of the whole operation.
The Bletchley Park example illustrates that even where it might appear to be good (and possible through secrecy regulations) for an organization to have people unaware of the big picture and their place in it, people in organizations just aren't that way. Awareness is ever present.
There will, of course, be some models in which individual decision rules can be simple and mindless instead of complicated and mindful. Game theory, and in particular evolutionary game theory, has exactly the ability to model simple agents where that is called for. Game theory, however, is uniquely positioned to model mindfulness and self-awareness in decision making and the systems that emerge from that in the many cases where it is appropriate.
The epitome of reductionism
It appears that one of the appeals of complexity/chaos is that it somehow rejects reductionism:
These results [of complexity] are rather counter-intuitive to those of us brought up on the reductionist assumption that knowing all about the parts will enable us to understand the whole. In complex systems the whole shows behaviors which cannot be gleaned by examining the parts alone. (McKergow, 1996: 722)
One widely distributed version of the call for papers for a special issue on complexity for the journal Organization Science stated:
Complexity theorists share a dissatisfaction with the “reductionist” science of the past, and a belief in the power of mathematics and computer modeling to transcend the limits of conventional science.
Unfortunately for those who seek antireductionism in complexity/chaos, it just isn't there in any interesting sense. But without digressing too far, we do need to clarify what is actually meant by “reductionism.” Richard Dawkins (1986: 13) has described the use of the word well:
If you read trendy intellectual magazines, you may have noticed that “reductionism” is one of those things, like sin, that is only mentioned by people who are against it. To call oneself a reductionist will sound, in some circles, a little like admitting to eating babies. But, just as nobody actually eats babies, so nobody is really a reductionist in any sense worth being against. The nonexistent reductionist—the sort that everybody is against, but who exists only in their imaginations—tries to explain complicated things directly in terms of the smallest parts, even, in some extreme versions of the myth, as the sum of the parts! [emphasis in original]
Elaborating on Dawkins and also on Dennett (1995: 80-83), we distinguish among three uses of the word “reductionism” as either a philosophy or a pejorative:
Type I Reductionism is the belief that one can offer an explanation of phenomena in terms of simpler entities or things already explained and the interactions between them.
Type II A system or theory is reductionist if the components are additive, but there are no interactions between the parts.
Type III A theory or explanation is reductionist if it seeks to explain macro-level phenomena directly in terms of the most basic elements without recourse to intermediate levels.
In much of our discussion of reductionism, we are following Dennett (1995: 80-83). We agree with Dennett that reductionism Type I is a good thing. Any theory or explanation that is not reductionistic in that sense is simply question begging or mystical. An explanation that is not in terms of simpler things or things already explained and the interactions between them fails to be an explanation.
Reductionism Type II is simply not very interesting. While there are some systems that are reductionistic in that sense and many more that aren't, it does not present any interesting or disputed boundary between different ways of investigating the world. By this type of definition an analysis that uses linear regression would be reductionist, while one that uses ANOVA would be nonreductionist. We suspect that this notion of reductionism is little more than a straw man. Neither game theory, complexity theory, nor chaos is reductionist in this sense. They all deal with interactions.
Reductionism Type III is what Dennett (1995: 82) calls “greedy reductionism.” It is the attempt to explain things without recourse to intermediate levels. A meteorologist who tried to explain the weather directly in terms of the motions of billions of molecules instead of talking about the intermediate levels of air masses, humidity, and the like might be guilty of greedy reductionism. A slightly less pejorative term for this might be “eliminative reductionism.”
In the rest of this discussion we will ignore the straw man of reductionism Type II and just consider the two other types.
Here we do need to examine chaos and complexity separately. First, we will look at the easy case: chaos. Before developments in chaos theory, certain nonlinear systems were simply not studied because they were too hard. Chaos theory has allowed researchers to make some sorts of predictions about the attractors and equilibria of these difficult systems. Chaos does not represent a retreat from the domain of Newtonian determinism, but an advance. It does not say that there are fewer things that we can talk about and make predictions about; instead, it gives us tools to talk about things that previously were too difficult to consider. Chaos theory expands the domain of reductionist (Type I) analysis:
When one observes collective behavior that exhibits instability over slight variations one typically assumes that an explanation must be equally complex. Traditionally, one expects simple behavioral outcomes from simple processes, and complex outcomes from complex processes. However, recent developments in chaotic dynamics show that a simple deterministic system [emphasis added] that is nonlinear can produce extremely complex and varied outcomes over time. (Richards, 1990: 219)
Chaos, then, is about finding simple underlying models for complicated phenomena. It expands the domain of what can be explained by simple models.
What about complexity? One contrast between game theory and complexity theory is that the latter usually relies on very simple agents with no self-reflection, as discussed earlier. Game theory allows for more sophisticated agents. Complexity is very specifically about generating macroscopic-level phenomena directly in terms of the many interactions of simple parts, often with little concern for developing theories about intermediate constructs. Clearly, complexity is more reductionistic in the sense of Type III. It appears that Dawkins may have been mistaken when he said that nobody really is reductionistic in the sense of trying “to explain complicated things directly in terms of the smallest parts” (Dawkins, 1986: 13); complexity theorists may be real examples of Type III reductionists!
Anyone who seeks antireductionism in chaos or complexity is bound to be disappointed. For us, however, their reductionism is appealing.
CONCLUSION
Our critique of complexity/chaos has been concerned with the rhetoric and with incorrect claims about what they entail. Once the rhetoric has been removed and the real tools are seen for what they are, we see true value in applying them to the study of management. Using complexity/chaos means constructing explicit models of the systems in question. In another domain, theoretical biology, Maynard Smith (1989) describes the utility of formal models (as opposed to what Saloner (1991: 127) calls the “boxes-and-arrows variety”):
There are two reasons why simple mathematical models are helpful in answering such questions. First, in constructing such a model, you are forced to make your assumptions explicit—or, at the very least, it is possible for others to discover what you assumed, even if you are not aware of it. Second, you can find out what is the simplest set of assumptions that will give rise to the phenomenon that you are trying to explain.
Saloner (1991) points out additional benefits of formal models, including that they can be built on and that they can lead to novel insights through surprising results.
We suspect, however, that many management scholars who currently find complexity/chaos appealing will find it less appealing, and even distasteful, if we do manage to persuade them that complexity/chaos is not a challenge to traditional science, but instead constitutes analytical tools allowing traditional science and modeling to be extended to domains that were previously too difficult.
If the explicit modeling of complexity is removed, it is disturbing to imagine what will actually remain.
FEAR OF GAMES
It may seem puzzling that a field is willing to embrace complexity theory and makes little use of its near equivalent, game theory. We have neither the data nor the space to provide a detailed argument as to why this discrepancy exists, but that won't prevent us from engaging in some brief speculation.
The expanding domain of economics
Many social sciences are under “threat” from the expansion of the economists' way of thinking and analysis into their domains. While the expansion has been going on for a while, it has been described explicitly by Hirshleifer (1985). At a recent workshop (ELSE, 1997) on the evolution of utility functions involving economists, biologists, some cognitive psychologists and anthropologists, and three management scholars, economist John Hey expressed some disappointment. He had expected to learn some methods and perspectives from the biologists, but instead discovered that they were just doing some (dated) economics.
Fear of this expansion can lead to management scholars trying to build walls around their domain by exaggerating the differences, which “incites a level of fear” (Hesterley and Zenger, 1993: 497). This would include demonizing the encroaching forces. Markóczy and Goldberg (1997: 409) argue that management scholars should be doing exactly the opposite:
We will have to learn how to enter into dialogue with scholars from other social sciences. Even if we ultimately reject the assumptions and approaches of those fields, we need to understand why those approaches are attractive to other scholars instead of merely searching for ways to dismiss them quickly.
This will be a difficult transition and it will meet with much internal resistance. But it isnecessary. As soon as this interdisciplinary group extends their study of cooperation to organizations, they will develop theories of organizations and behavior within them which will be attractive to anthropologists, biologists, cognitive scientists, economists, philosophers, and psychologists. As they are making great gains in discovering the nature of cooperation, management scholars ought to be working with them.
We believe that a renewed interest among management scholars in modeling human systems provides a step toward that interdisciplinary integration. Those who resist the encroachment of economics (or fields that have adopted many of their methods) will be reluctant to build explicit models, or will try to call them by other names when they do.
The snake swallows its own tail
Everyone loves a self-referential paradox: a rule or a system that turns in on itself or proves its own impossibility. If that system is thought to be cold, cruel, an authority, and a power, then it is even better if it contains the seeds of its own destruction. Those who maintain this view of traditional science will naturally delight in the claims of complexity/chaos.
From a theoretical perspective, chaos theory is congruous with the postmodern paradigm, which questions deterministic positivism as it acknowledges the complexity and diversity of experience. (Levy, 1994: 168)
We accept neither their view of science nor those claims of complexity/chaos. Chaos and complexity do not pose a serious challenge to science and prediction; and science has always been concerned with the interactions of parts.
Abuse of science
Some of the attraction of (mis)using chaos and complexity theory in the study of management has little to do with particular details of the theories, but may be part of a broader pattern of abuse of physical and mathematical sciences in the humanities and social sciences. Sokal and Bricmont (1998: 4) describe that sort of abuse and make an attempt at defining it:
The word “abuse” here denotes one or more of the following characteristics:
- Holding forth at length on scientific theories about which one has, at best, an exceedingly hazy idea. The most common tactic is to use scientific (or pseudo-scientific) terminology without bothering much about what the words actually mean.
- Importing concepts from the natural sciences into the humanities or social sciences without giving the slightest conceptual or empirical justification. If a biologist wanted to apply, in her research, elementary notions of mathematical topology, set theory or differential geometry, she would be asked to give some explanation. A vague analogy would not be taken very seriously by her colleagues…
- Displaying a superficial erudition by shamelessly throwing around technical terms in a context where they are completely irrelevant. The goal is, no doubt, to impress and, above all, to intimidate the nonscientific reader…
- Manipulating phrases and sentences that are, in fact, meaningless. Some of these authors exhibit a veritable intoxication with words, combined with a superb indifference to their meaning.
While Sokal and Bricmont (1998) were largely discussing other abuses, they do include a chapter (Chapter 7) on “chaos theory and ‘postmodern science,'” which covers some of the same material and misunderstandings we discuss above.
Rational concerns
Some of the objections that are occasionally raised in relation to game theory are that it requires absurd assumptions of rationality. This simply isn't true. The introductory exercises and examples given usually do involve very strong rationality assumptions, but once one understands how to use game theory, it is possible to relax those assumptions substantially (Camerer, 1991). Evolutionary game theory involves agents, such as bees and trees, with exceedingly limited rationality; and behavioral game theory specifically seeks to work with agents that have empirically verified types of human rationality (Camerer, 1997).
IT'S NOT WHETHER YOU WIN OR LOSE BUT HOW YOU LAY THE BLAME
In looking at some of the literature on chaos/complexity we find misleading and incorrect statements. But we also find that many of those arise not from the misinterpretations of management scholars, but from the popularizations of complexity/chaos itself. When complexity proponents make statements suggesting a radical new paradigm for all sciences including the social sciences, it is no wonder that some of those in search of a radical new paradigm will follow.
Some complexity workers very strongly exaggerate the difference between what they do and what evolutionary game theorists do. At a seminar organized by the Research Centre for Economic Learning and Social Evolution (March, 1997), John Holland argued forcefully that the model he presented could not be treated game theoretically because “the rules changed.” However, a superficial glance at his model showed that what he called “rules” map into what game theory calls “strategies,” which can and do change.
In other cases, popularizers have been more careful, but have still left areas open for misunderstanding. For example, most of the discussion by Gleick (1996) treats the issues of determinism and nondeterminism correctly. However, Gleick does indeed quote people whose statements do suggest that chaos overturns determinism. He does not appear to notice the contradiction and takes no corrective action. People seeking a radical challenge to traditional science will pick up on those few quotes and entirely ignore most of the rest of the book's insistence that those systems are deterministic.
It is natural for any stream of research to overstate the differences between it and its rivals, but it is also the responsibility of the rest of the academic community to look through the rhetoric and examine the real claims and identify what is of real value. We hope we have helped fulfill that responsibility.
To add one more paradox to this article, we note that our challenge to complexity and chaos as reported in the management literature is partially motivated by our sympathy with chaos and some parts of complexity in general.The benefits to fields outside of the social sciences of the study of nonlinear dynamical systems are too numerous to mention. Some of the best work in complexity (e.g., Axelrod, 1997; Sigmund, 1993; Schelling, 1978) eschews the worst of the rhetoric and has helped raise the awareness of what can be reached with very simple agents. It is our appreciation of the better parts of this work that drives us to discourage management scholars from using misunderstood slogans from these fields and to encourage people to show these areas due respect by either really learning about them or remaining silent.
REFERENCES
Abraham, R. H. and Shaw, C. D. (1983) Dynamics: The Geometry of Behavior: Periodic Behavior, Vol. 1 of The Visual Mathematics Library, Santa Cruz, CA: Aerial Press.
Axelrod, R. (1984) The Evolution of Cooperation, New York, NY: Basic Books.
Axelrod, R. M. (1997) The Complexity of Cooperation: Agent-based Models of Competition and Collaboration, Princeton Studies on Complexity, Princeton, NJ: Princeton University Press.
Axelrod, R., Mitchell, W., Thomas, R. E., Scott Bennett, D., and Bruderer, E. (1997) “Coalition formation in standard-setting alliances,” in Axelrod, R., The Complexity of Cooperation: Agent-based Models of Competition and Collaboration, Princeton Studies on Complexity, Princeton, NJ: Princeton University Press, Chapter 5, 96-120. (Article originally appeared in Management Science, 41, 1995).
Axelrod, R. and Scott Bennett, D. (1997) “A landscape theory of aggregation,” in Axelrod.
R.M. (1997) The Complexity of Cooperation: Agent-based Models of Competition and Collaboration, Princeton Studies on Complexity, Princeton, NJ: Princeton University Press, Chapter 4, 72-94. (Article originally appeared in British Journal of Political Science, 23, 1993.)
Binmore, K. (1982) Fun and Games, Lexington, MA: Heath.
Binmore, K. (1994) Game Theory and the Social Contract, Volume I: Playing Fair, Cambridge, MA: MIT Press.
Binmore, K. (1998) Review of Robert Axelrod'ss The Complexity of Cooperation, Journal of Artificial Societies and Social Simulation, 1 (1), electronic journal published at http:\www.soc.surrey.ac.uk\expndtw-3 JASSS.
Brown, A. (1999) The Darwin Wars: How Stupid Genes Became Selfish Gods, London: Simon and Schuster.
Brown, S. L. and Eisenhardt, K. M. (1997) “The art of continuous change: linking complex- ity theory and time-paced evolution in relentlessly shifting organizations,” Administrative Science Quarterly, 42 (1): 1-34.
Camerer, C. E. (1991) “Does strategy research need game theory?” Strategic Management Journal, 12: 137-52.
Camerer, C. E. (1997) “Progress in behavioral game theory,” Journal of Economic Perspectives, 11 (4): 167-88.
Cheng, Y.-T. and Van de Ven, A. H. (1996) “Learning the innovation journey: order out of chaos?” Organization Science, 7 (6): 593-614.
Cohen, J. and Stewart, I. (1994) The Collapse of Chaos: Discovering Simplicity in a Complex World, London: Penguin.
David, P. A. (1985) “Clio and the economics of QWERTY,” American Economic Review, 75: 332-7.
Dawkins, R. (1986) The Blind Watchmaker, New York, NY: Norton.
Dennett, D. C. (1995) Darwin'ss Dangerous Idea: Evolution and the Meaning of Life, London: Penguin.
Dixit, A. K. and Nalebuff, B.J. (1991) Thinking Strategically: The Competitive Edge inBusiness, Politics, and Everyday Life, New York, NY: Norton.
*Economist *(1998) “Unscientific readers of science,” The Economist, 347 (8067): 129-30.
ELSE (1997) Workshop on the evolution of utility, Research Centre for Economic Learning and Social Evolution, University College London.
Elster, J. (1989) The Cement of Society: A Study of Social Order, Studies in Rationality and Social Change, Cambridge: Cambridge University Press.
Gibbons, R. (1992) Game Theory for Applied Economists, Princeton, NJ: Princeton University Press.
Gibbons, R. (1997) “An introduction to applicable game theory,” Journal of Economic Perspectives, 11 (1): 127-50.
Ginsberg, A., Larsen, E., and Loni, A. (1996) “Generating strategy from individual behavior: a dynamic model of structural embeddedness,” in P. Shrivastava, A. Huff, and J. Dutton (eds) Advances in Strategy Management, Vol. 9, Greenwich, CT: JAI Press, 121-47.
Gleick, J. (1996) Chaos, London: Minerva.
Goldberg, J. and Markóczy, L. (1997) “Symmetry: time travel, mind-control and other every- day phenomena required for cooperative behavior,” paper presented at Academy of Management Conference, Boston.
Hartmanis, J. and Hopcroft, J. E. (1971) “An overview of the theory of computational com- plexity,” Journal of the Association for Computing Machinery, 18: 444-75.
Hesterley, W. S. and Zenger, T. R. (1993) “The myth of a monolithic economics: fundamen- tal assumptions and the use of economic models in policy and strategy research,” Organization Science, 4 (3): 496-510.
Hirshleifer, J. (1985) “The expanding domain of economics,” American Economic Review, 75 (6): 53-70.
Hirshleifer, J. and Coll, J. C. M. (1988) “What strategies can support the evolutionary emer- gence of cooperation,” Journal of Conflict Resolution, 32 (2): 367-98.
Holland, J. H. (1995) Hidden Order: How Adaptation Builds Complexity, New York, NY: Addison-Wesley.
Johnson, J. L. and Burton, B. K. (1994) “Chaos and complexity theory in management: caveat emptor,” Journal of Management Inquiry, 3 (4): 320-28.
Johnston, M. (1996) A book review of Alex Trisoglio, “Managing complexity,” working paper 1 in the LSE research programme on complexity, Long Range Planning, 29 (4): 588-9. Kavka, G. S. (1987) Moral Paradoxes of Nuclear Deterrence, Cambridge: Cambridge University Press.
Kay, J. (1993) Foundations of Corporate Success: How Business Strategies Add Value, Oxford: Oxford University Press.
Kreps, D. M. (1990) Game Theory and Economic Modelling, Oxford: Oxford University Press.
Levy, D. (1994) “Chaos theory and strategy: theory, application, and managerial implica- tions,” Strategic Management Journal, 15: 167-78.
Liebowitz, S. J. and Margolis, S. E. (1990) “The fable of the keys,” Journal of Law and Economics, 33.
Lorenz, E. (1963) “Deterministic nonperiodic flow,” Journal of Atmospheric Sciences, 20: 130.
Markóczy, L. and Goldberg, J. (1997) “The virtue of cooperation: a review of Ridley'ss Origins of Virtue,” Managerial and Decision Economics, 18: 399-411.
May, R. M. (1976) “Simple mathematical models with very complicated dynamics,” Nature, 261: 457-67.
Maynard Smith, J. (1989) “Natural selection of culture,” in J. Maynard Smith (ed.) Did Darwin Get It Right? Essays on Games, Sex and Evolution, New York, NY: Chapman and Hall. (First published as a review of R. Boyd and D. Richarson'ss *Culture and the Evolutionary Process *in the New York Review of Books, November 1986.)
McKergow, M. (1996) “Complexity science and management: what'ss in it for business,” Long Range Planning, 29 (5): 721-7.
McMillan, J. (1992) Games, Strategies and Management, Oxford: Oxford University Press. Meiss, J. D. (1998) Nonlinear science FAQ: Frequently asked questions about nonlinear science, chaos, and dynamical systems, version 1.1.9, Internet newsgroup (Usenet) FAQ. (This and all Usenet FAQs are available via FTP from rtfm.mit.edu in the directory as well as from many other archive sites.)
Parker, D. and Stacey, R. (1994) Chaos, Management and Economics: The Implication of Non-linear Thinking, London: Institute of Economic Affairs.
Payne, D. (1993) “The bombes,” in F. H. Hinsley and A. Stripp (eds) Codebreakers: The Inside Story of Bletchley Park, Oxford: Oxford University Press, 132-7.
Poundstone, W. (1992) Prisoner's Dilemma: John von Neumann, Game Theory, and the Puzzle of the Bomb, New York: Doubleday.
Rapoport, A. (1966) Two-person Game Theory: The Essential Ideas, Ann Arbor, MI: University of Michigan Press.
Richards, D. (1990) “Is strategic decision making chaotic?” Behavioral Science, 35: 219-32.
Saloner, G. (1991) “Modeling, game theory, and strategic management,” Strategic Management Journal, 12: 119-36.
Schelling, T. C. (1978) Micromotives and Macrobehavior, New York, NY: Norton.
Schelling, T. C. (1980) The Strategy of Conflict, Cambridge, MA: Harvard University Press.
Sigmund, K. (1993) Games of Life: Explorations in Ecology, Evolution and Behavior, Oxford: Oxford University Press.
Sokal, A. and Bricmont, J. (1998) Intellectual Impostures: Postmodern Philosophers' Abuse of Science, London: Profile Books.
Stacey, R. (1991) The Chaos Frontier: Creative Strategic Control for Business, Oxford: Butterworth Heinemann.
Stacey, R. D. (1995) “The science of complexity: an alternative perspective for strategic change processes,” Strategic Management Journal, 16 (6): 477-95.
Van de Ven, A. H. and Scott Poole, M. (1995) “Explaining development and change in organ- izations,” Academy of Management Review, 20 (3): 510-40.