HOW WE KNOW UNIVERSALS THE PERCEPTION OF AUDITORY AND VISUAL FORMS1 [76]
W. Pitts and W.S. McCulloch
Abstract
Two neural mechanisms are described which exhibit recognition of forms. Both are independent of small perturbations at synapses of excitation, threshold, and synchrony, and are referred to particular appropriate regions of the nervous system, thus suggesting experimental verification. The first mechanism averages an apparition over a group, and in the treatment of this mechanism it is suggested that scansion plays a significant part. The second mechanism reduces an apparition to a standard selected from among its many legitimate presentations. The former mechanism is exemplified by the recognition of chords regardless of pitch and shapes regardless of size. The latter is exemplified here only in the reflexive mechanism translating apparitions to the fovea. Both are extensions to contemporaneous functions of the knowing of universals heretofore treated by the authors only with respect to sequence in time.
Introduction
To demonstrate existential consequences of known characters of neurons, any theoretically conceivable net embodying the possibility will serve. It is equally legitimate to have every net accompanied by anatomical directions as to where to record the action of its supposed components, for experiment will serve to eliminate those which do not fit the facts. But it is wise to construct even these nets so that their principal function is little perturbed by small perturbations in excitation, threshold, or detail of connection within the same neighborhood. Genes can only predetermine statistical order, and original chaos must reign over nets that learn, for learning builds new order according to a law of use.
Numerous nets, embodied in special nervous structures, serve to classify information according to useful common characters. In vision they detect the equivalence of apparitions related by similarity and congruence, like those of a single physical thing seen from various places. In audition, they recognize timbre and chord, regardless of pitch. The equivalent apparitions in all cases share a common figure and define a group of transformations that take the equivalents into one another but preserve the figure invariant. So, for example, the group of translations removes a square appearing at one place to other places; but the figure of a square it leaves invariant. These figures are the geometric objects of Cartan and Weyl, the Gestalten of Wertheimer and Köhler. We seek general methods for designing nervous nets which recognize figures in such a way as to produce the same output for every input belonging to the figure. We endeavor particularly to find those which fit the histology and physiology of the actual structure.
The epicritical modalities map the continuous variables of sense into the neurons of a fine cortical mosaic that strikingly imitates a continuous manifold. The visual half-field is projected continuously to the area striata, and tones are projected by pitch along Heschl's gyrus. We can describe such a manifold, say 𝓜, by a set of coordinates (x1, x2, … , xn) constituting the point-vector x, and denote the distributions of excitation received in 𝓜 by the functions ϕ(x, t) having the value unity if there is a neuron at the point x which has fired within one synaptic delay prior to the time t, and otherwise, the value zero. For simplicity, we shall measure time in mean synaptic delays, supposed equal, constant, and about a millisecond long. Indications of time will often not be given.
Let G be the group of transformations which carry the functions ϕ(x, t) describing apparitions into their equivalents of the same figure. The group G may always be taken finite, as is seen from the atomicity of the manifold; let it have N members. We shall distinguish four problems of ascending complexity:
- The transformation T of G can be generated by transformations t of the underlying manifold 𝓜, so that Tϕ(x) = ϕ[t(x)]; e.g., if G is the group of translations, then Tϕ(x) = ϕ(x + αT), where αT is a constant vector depending only upon T. If G is the group of dilatations, Tϕ(x) = ϕ(αTx), where αT is a positive real number depending only upon T. All such transformations are linear:
T[αϕ(x) + βψ(x)]=αϕ[t(x)] + βψ[t(x)]
= αTϕ(x) + βTψ(x).
- The transformations T of G cannot be so generated, but are still linear and independent of the time t. An example is to take the gradient of ϕ(x), or to replace ϕ(x) by its average over a certain circle surrounding x.
- The transformations T of G are linear, but depend also upon the time. For example, they take a moving average over the preceding five synaptic delays or take some difference as an approximation to the time-derivative of ϕ(x, t).
- Not all T of G are linear.
Our special nets are essays in problem 1. The simplest way to construct invariants of a given distribution ϕ(x,t) of excitation is to average over the group G. Let f be an arbitrary functional which assigns a unique numerical value, in any way, to every distribution ϕ(x, t) of excitation in 𝓜 over time. We form every transform Tϕ of ϕ(x, t), evaluate t[Tϕ] and average the result over G to derive
If we had started with Sϕ, S of G, instead of ϕ, we should have
for TS-1 is in the group when, and only when, T is in the group; that is, the terms of the sum (1) are merely permuted.
To characterize completely the figure of ϕ (x, t) under G by invariants of this kind, we need a whole manifold Ξ of such numbers a for different functionals f, with as many dimensions in general as the original 𝓜; if we describe Ξ by coordinates (ξ1, ξ2, …, ξn) = ξ, we may fulfill this requirement formally with a single f which depends upon £ as a parameter as well as upon the distribution ϕ which is its argument, and write
If the nervous system needs less than complete information in order to recognize shapes, the manifold Ξ may be much smaller than 𝓜, have fewer dimensions, and indeed reduce to isolated points. The time t may be one dimension of Ξ, as may some of the xj representing position in 𝓜.
Suppose that G belongs to problems 1 or 2 and that the dimensions of Ξ are all spatial; then the simplest nervous net to realize this formal process is obtained in the following way: Let the original manifold 𝓜 be duplicated on N—1 sheets, a manifold 𝓜τ for each T of G, and connected to 𝓜 or its sensory afferents in such a way that whatever produces the distribution ϕ(x) on 𝓜 produces the transformed distribution Tϕ(x) on 𝓜τ. Thereupon, separately for each value of ξ for each 𝓜τ, the value of f[Tϕξ] is computed by a suitable net, and the results from all the 𝓜τ's are added by convergence on the neuron at the point £ of the mosaic Ξ. But to proceed entirely in this way usually requires too many associative neurons to be plausible. The manifolds 𝓜τ together possess the sum of the dimensions of 𝓜 and the degrees of freedom of the group G. More important is the number of neurons and fibers necessary to compute the values of f[Tϕ, ξ], which depends, in principle, upon the entire distribution Tϕ, and therefore requires a separate computer for every ξ for every T of G. This difficulty is most acute if f be computed in a structure separated from the 𝓜τ, since in that case all operations must be performed by relatively few long fibers. We can improve matters considerably by the following device: Let the manifolds 𝓜τ be connected as before, but raise their thresholds so that their specific afferents alone are no longer able to excite them; cause adjuvant fibers to ramify throughout each 𝓜τ so that when active they remedy the deficiency in summation and permit 𝓜τ to display Tϕ(x) as before. Let all the neurons with the same coordinate x on the N different 𝓜τ's send axons to the neuron at x on another recipient sheet exactly like them, say Q — this Q may perfectly well be one of the 𝓜τ — and suppose any one of them can excite this neuron. If the adjuvant neurons are excited in a regular cycle so that every one of the sheets 𝓜τ in turn, and only one at a time, receives the increment of summation it requires for activity, then all of the transforms Tϕ of ϕ(x) will be displayed successively on Q. A single f computer for each ξb taking its input from Q instead of from the Mr's, will now suffice to produce all the values of f[Tϕ, ξ] in turn as the “time-scanning” presents all the Tø's on Q in the course of a cycle. These values of f(Tϕ, ξ) may be accumulated through a cycle at the final Ξ-neuron in any way.
This device illustrates a useful general principle which we may call the exchangeability of time and space. This states that any dimension or degree of freedom of a manifold or group can be exchanged freely with as much delay in the operation as corresponds to the number of distinct places along that dimension.
Let us consider the auditory mechanism which recognizes chord and timbre independent of pitch. This mechanism, or part of it, we shall suppose situated in Heschl's gyrus, a strip of cortex two to three centimeters long on the superior surface of the temporal lobe. This strip receives afferents from lower auditory mechanisms so that the position on the cortex corresponds to the pitch of tones, low tones exciting the outer and forward end, high tones the inner and posterior. Octaves span equal cortical distances, as on the keyboard of a piano. The afferents conveying this information from the medial geniculate slant upward through the cortex, branching into telodendria in the principal recipient layer IV, which consists of vertical columns of fifty or more neurons concerning the course of whose ramifying axons there is no certain knowledge except that their activity eventually excites columns of cells situated beneath the recipient layers. Their axons converge to a layer of small pyramids whose axons terminate principally in the secondary auditory cortex or adjacent parts of the temporal lobe. To the layers above and below the receptive layers also come “associative” fibers from elsewhere in the cortex, particularly from nearby. There is no good Golgi picture of the primary auditory cortex in monkeys, but unless it is unlike all the rest of the cortex, it also receives nonspecific afferents from the thalamus, which ascend to branch indiscriminately at every level. A picture of the primary auditory cortex stained by Nissl's method is given in Figure 1, and a schematic version in Figure 2.

Figure 1. Vertical section of the primary auditory cortex in the long axis of Heschl's gyrus, stained by Nissl's method which stains only cell bodies. Note that the columnar cortex, typical of primary receptive areas, shows two tiers of columns, the upper belonging to the receptive layer IV and the lower, lighter stained, to layer V.
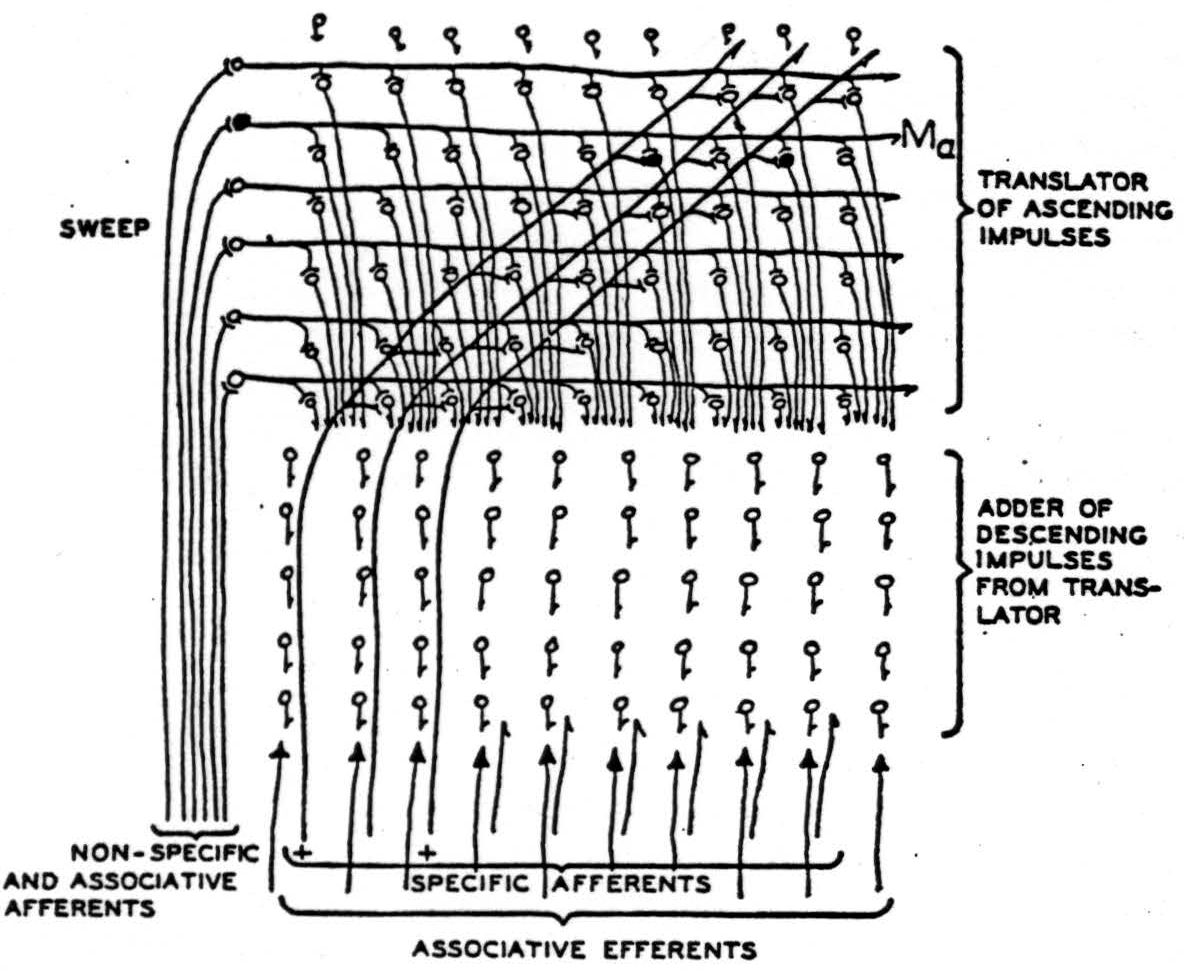
Figure 2. Impulses of some chord enter slantwise along the specific afferents, marked by plusses, and ascend until they reach the level 𝓜a in the columns of the receptive layer activated at the moment by the nonspecific afferents. These provide summation adequate to permit the impulses to enter that level but no other. From there the impulses descend along columns to the depth. The level in the column, facilitated by the nonspecific afferents, moves repetitively up and down, so that the excitement delivered to the depths moves uniformly back and forth as if the sounds moved up and down together in pitch, preserving intervals. In the deep columns various combinations are made of the excitation and are averaged during a cycle of scansion to produce results depending only on the chord.
The secondary auditory cortex has separate specific afferents and the same structure as the primary except for possessing some large pyramids known to send axons to distant places in the cortex such as the motor face and speech areas.
In this case, the fundamental manifold 𝓜 is a one-dimensional strip, and x is a single coordinate measuring position along it. The group G is the group of uniform translations which transform a distribution ϕ(x, t) of excitation along the strip into Taϕ = ϕ (x + a,t). The group G is thus determined by adding the various constants to the coordinate x, and therefore belongs to problem 1. The set of manifolds 𝓜T is a set of strips 𝓜a that could be obtained by sliding the whole of 𝓜a back and forth various distances along its length. The same effect is obtained by slanting the afferent fibers upward, as in Figure 2, and in the auditory cortex itself where the levels in the columnar receptive layer constitute the 𝓜T. These send axons to the deeper layer, a mass capable of reverberation and summation over time, that may well constitute the set of f(T ϕ, ξ) computers for the various ξ, or part of them.
To complete the parallel with our general model, we require adjuvant fibers to activate the various levels 𝓜a successively. It is to the nonspecific afferents that modern physiology attributes the well- known rhythmic sweep of a sheet of negativity up and down through the cortex—the alpha-rhythm. If our model fits the facts, this alpha- rhythm performs a temporal “scanning” of the cortex which thereby gains, at the cost of time, the equivalent of another spatial dimension in its neural manifold.
According to Ramon y Cajal(1), Lorente de Nó(2), and J. L. O'Leary(3), the specific visual afferents originate in the lateral geniculate body and travel upward through the calcarine cortex, to ramify horizontally for long distances in the stripe of Gennari. This is called the granular layer by Brodmann from Nissl stains, and is also called the external stria of Baillarger, from its myeloarchitecture. (4). It is the fourth, or receptive, layer of Lorente de Nó. It may be divided into a superior part IVa, consisting of the larger star-cells and star-pyramids, and an inferior part IVb, consisting of somewhat smaller star-cells, arranged in columns, although the distinction of parts is not always evident(3). The stripe of Gennari is the sole terminus of specific afferent fibers in the cat and higher mammals, although not in the rabbit. Its neurons send numerous axons horizontally and obliquely upward and downward within the layer; others ascend to the plexiform layer at the surface or descend to the subjacent fifth layer of efferent cells; and axons from the large star-pyramids even enter the subjacent white matter.
The electrical records of J. L. O'Leary and G. H. Bishop(3) indicate that the normal response of the striate cortex to an afferent volley is triphasic, commencing in layer IV, shown by a surface-positive potential. Next it rises to the surface, making it negative; then as the surface becomes positive, it descends first to the third layer to project to other cortical areas, and then reaches the fifth layer, whence it goes to the pulvinar, the superior colliculus(5), and tegmental oculo-motor nuclei, especially to the para-abducens nucleus, which subserves conjugate deviation of the eyes. (Personal communication from Elizabeth Crosby.) This triphasic response, having the period of the alpha-rhythm, is too long to be easily envisaged as a single cycle of purely internal reverberation in the striate cortex. This opinion is confirmed by the super imposed faster response to more intense afferent volleys. It is more reasonable to regard efferents to undifferentiated thalamic nuclei and nonspecific afferents from them(6) as responsible for the sustention of this triphasic rhythm. As in the auditory mechanism, we assign them the function of “scanning” by exciting sheets seriatim in the upper layers of the cortex.
A version of the visual cortex which agrees with these facts and which constitutes a mechanism of the present type for securing invariance to dilatation and constriction of visual forms is diagrammed in Figure 3. For comparison with this scheme some drawings by Cajal(7) from Golgi preparations are shown in Figure 4 with the original captions.
Figure 3 is a diagram of part of the neurons in a vertical section of cortex taken radially outward from that cortical point to which the center of the fovea projects. The lowest-tier of small cells in IVb is the primary receptive manifold 𝓜 the upper tiers of internuncials in I, II, and III, to which the upper tiers of layer IVa separately project, constitute the manifolds for uniform constriction of all the coordinates of an apparition by factors 0 < a < 1. This reduplication of the layers of IVa in additional upper intrnuncial tiers is of course unnecessary since the nonspecific afferents might equally well scan the layers of star-pyramids themselves. The magnifications of the apparition are represented on the internuncial tiers drawn beneath the efferents in the third layer. It is quite likely that these are in reality the small star-cells of IVb, or even the long horizontal extensions of the specific afferents within the outer stria of Baillarger. Histological sections of the visual cortex are now being cut radial to the projection of the center of the fovea and perpendicular to it. It is evident that many details of this and the other hypothetical nets of this paper might be chosen in several ways with equal reason; we have only taken the most likely in the light of present knowledge. The sheet of excitement from nonspecific afferents sweeping up and down the upper three layers, therefore, produces all magnifications and constrictions seriatim on the efferent cells of layer III, traveling from there to the parastriate cortex where the functionals f are made of them and the results added.
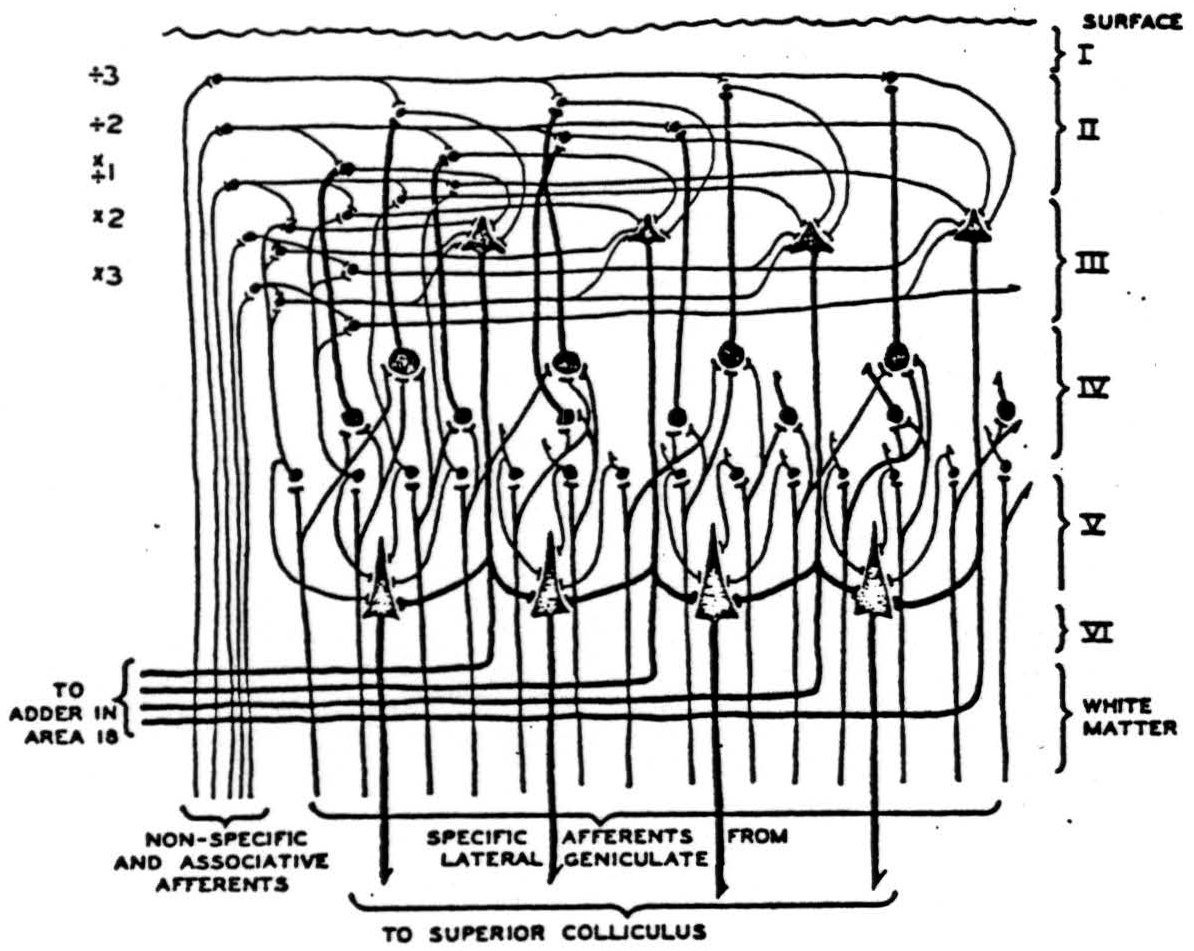
Figure 3. Impulses relayed by the lateral geniculate from the eyes ascend in specific afferents to layer IV where they branch laterally, exciting small cells singly and larger cells only by summation. Large cells thus represent larger visual areas. From layer IV impulses impinge on higher layers where summation is required from nonspecific thalamic afferents or associative fibers. From there they converge on large cells of the third layer which relay impulses to the parastriate area 18 for addition. On their way down they contribute to summation on the large pyramids of layer V which relays them to the superior colliculus.
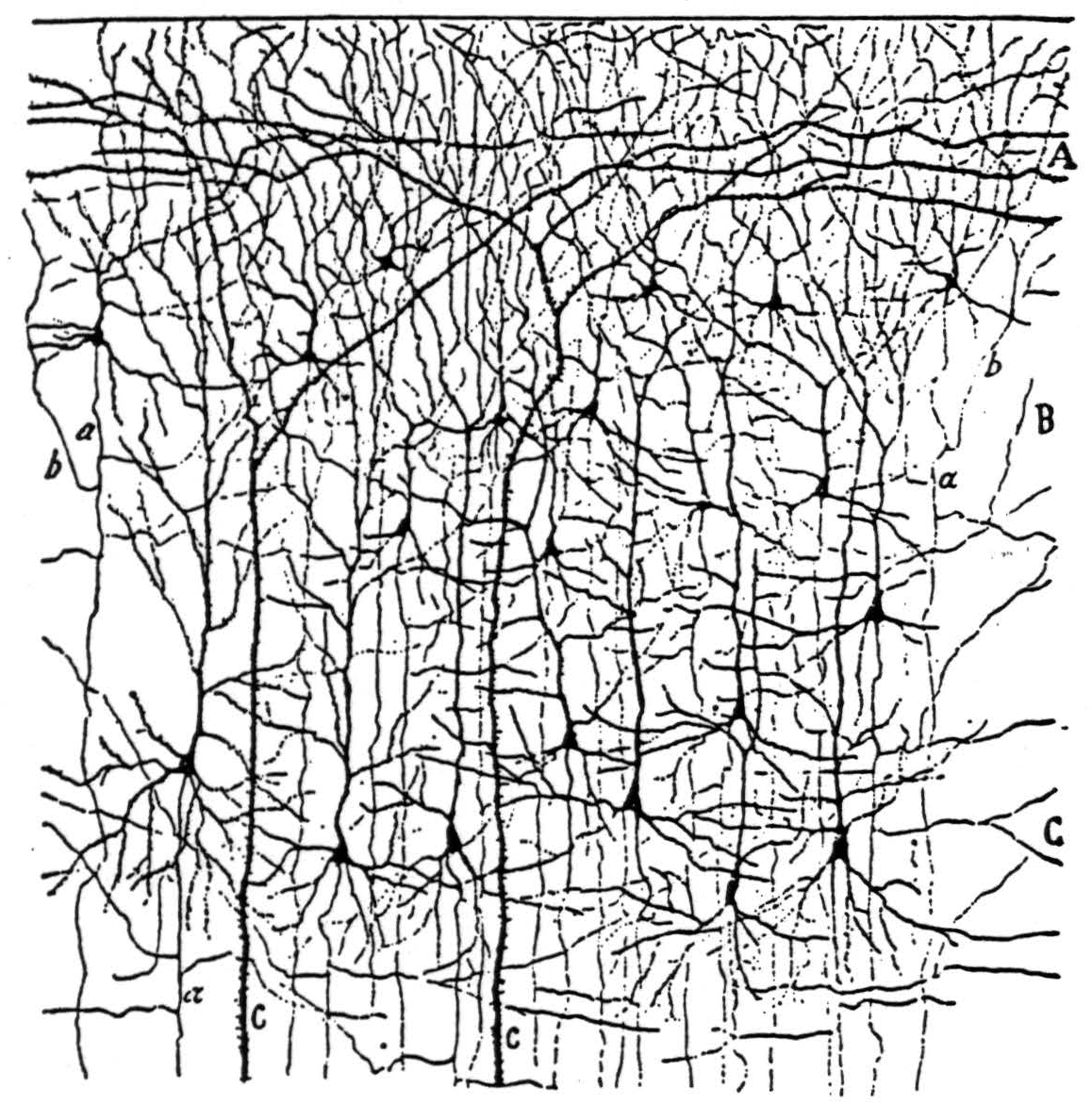
Figure 4a. The following is the original caption. Kleine und mittelgrosse Pyramidenzellen der Sehrinde eines 20 tägigen Neugeborenen (Fissura calcarina). A, plexiforme Schicht; B, Schicht der kleinen Pyramiden; C, Schicht der mittelgrossen Pyramiden; a, absteigender Axencylinder; b, rückläufige Collateralen; c, Stiele von Riesenpyramiden.
It is worth observing again, when special example can fix it, that the group-invariant spatio-temporal distribution of excitations which represents a figure need not resemble it in any simple way. Thus, purely for illustration, we might suppose that the efferent pyramids in the layer III of our diagram project topographically upon another cortical mosaic, which only responds to corners, and accumulates over a cycle of scansion. A square in the visual field, as it moved in and out in successive constrictions and dilatations in Area 17, would trace out four spokes radiating from a common center upon the recipient mosaic. This four-spoked form, not at all like a square, would then be the size-invariant figure of square. In fact, Area 18 does not act like this, for during stimulation of a single spot in the parastriate cortex, human patients report perceiving1 complete and well-defined objects, but without definite size or position, much as in ordinary visual mental imagery. This is why we have situated the mechanism of Figure 3 in Area 17, instead of later in the visual association system. This also makes it likely that one of the dimensions of the apperceptive manifold Ξ, upon whose points the group- averages of various properties of the apparition are summed, is time.

Figure 4b. The following is the original caption. Schichten der Sternzellen der Sehrinde des 20 tägigen Neugeborenen (Fissura calcarina). A, Schicht der grossen Stemzellen; a, halbmondförmige Zellen; b, horizontale Spindelzelle; c, Zellen mit einem zarten radiären Fortsatz; e, Zelle mit gebogenem Axencylinder; B, Schicht der kleinen Stemzellen; f, horizontale Spin-delzellen; g, dreieckige Zellen mit starken gebogenen Collateralen; h, Pyramiden mit gebogenem Axencylinder, an der Grenze der fünften Schicht; C, Schicht der kleinen Pyramiden mit gebogenem Axencylinder.
This point is especially to be taken against the Gestalt psychologists, who will not conceive a figure being known save by depicting it topographically on neuronal mosaics, and against the neurologists of the school of Hughlings Jackson, who must have it fed to some specialized neuron whose business is, say, the reading of squares. That language in which information is communicated to the homunculus who sits always beyond any incomplete analysis of sensory mechanisms and before any analysis of motor ones neither needs to be nor is apt to be built on the plan of those languages men use toward one another.
Besides the mechanisms which compute invariants as averages, there is another variety of nervous net that can perceive universals. These nets we call reflex-mechanisms. Consider the reflex-arc from the eyes through the tectum to the oculomotor nuclei and so to the muscles which direct the gaze. We propose that the superior colliculus computes by double integration the lateral and vertical coordinates of the “center of gravity of the distribution of brightness” referred to the point of fixation as origin, and supplies impulses at a rate proportional to these coordinates to the lateral and vertical eye-muscles in such a way that these then turn the visual axis toward the center of gravity. As the center of gravity approaches the origin, its ordinate and abscissa diminish, slowing the eyes and finally stopping them when the visual axes point at the “center of brightness.” This provides invariants of translation. If a square should appear anywhere in the field, the eyes turn until it is centered, and what they see is the same, whatever the initial position of the square. This is a reflex-mechanism, for it operates on the principle of the servo-mechanism, or “negative feedback.”
We find considerable support for this conjecture in the profuse anatomical and physiological literature on the corpora quatrigemina anteriora. Histologically, in mammals they are arranged in nine laminae, composed alternately of grey and white matter. Aside from the central grey of the aqueduct, we may enumerate these as follows, from the most superficial inward, naming them with C. V. Ariëns-Kappers, G. C. Huber, and E. C. Crosby(8):
- A superficial layer of fine white myelinated fibers running antero-posteriorly. These arise in the posterior end of the middle temporal gyrus, about Area 37 of Brodmann, in the part of the temporal lobe which associates visual and auditory material. (E. Crosby, unpublished.) This is the stratum zonale, so called by Cajal(1).
- A stratum griseum superficial, composed of radially directed cells of sundry types, each with dendrites ramifying near one or both of the adjacent layers, and an axon plunging down into the fourth layer.
- The stratum opticum. This dense layer of myelinated fibers courses antero-posteriorly and constitutes the major afferent supply to the colliculus. The upper portion comes directly from the optic chiasm, as fibers from the nasal side of the contralateral retina and the temporal side of the ipsilateral, and pierces the rostral surface. These direct fibers diminish in number and importance in the higher mammals, giving place to fibers from the occipital cortex beneath them in the layer. These come up from the depths with the radiation from Area 17 somewhat caudal to that from Area 18 or 19 or both(5). There are some other cortical fibers of unknown origin in this stratum also, but none from the frontal eye-fields of Area 8 (ibid.), which projects directly to oculomotor nuclei(9). The fibers of the stratum opticum end in bushy terminal arborizations in the grey matter above and below it.
- A stratum griseum mediate, which, together with the three laminae beneath—the stratum album mediate, and the two strata alba et grisea profunda—makes up Cajal's(1) “Zone ganglionaire ou des fibres horizontales.” Here lie the principal bigeminate efferents. The dendrites of these cells pervade the reach their somata from all the upper strata and the commissure of the superior colliculus. Their axons course horizontally, laterally, and then somewhat caudally, descend to the stratum album profundum, and leave the tectum laterally or else pierce the medial surface as commissural fibers to the other colliculus. The former comprises the “uncrossed” bundle of tecto-pontine fibers (not tecto-spinal: ibid.) besides the main “voie optique reflexe” of Cajal. The latter leaves the tectum to spiral ventrad and caudad around the aqueduct and the third and the fourth nerve nuclei, decussates. and passes caudad under the medial longitudinal fasciculus to the para-abducens and Vl-th nerve nuclei, and to the cervical cord(1). As it passes, it gives collaterals to all the oculomotor nuclei, mostly crossed at the rostral end and mostly uncrossed posteriorly (E. Crosby, unpublished). As we proceed caudally, the oculomotor nuclei innervate the ocular muscles, in this order: superior rectus, medial rectus, inferior oblique, inferior rectus, and thence the superior oblique and the lateral rectus, substantiating the scheme of B. Brouwer(10). These nuclei are interconnected by the medial longitudinal fasciculus, whereby axonal collaterals presumably inhibit antagonists and facilitate synergists. They are aided in this by modest interstitial nuclei such as the para-abducens, subserving conjugate deviation, and perhaps one between the medial recti, for convergence. Such nuclei also serve to transmit the cortical, striatal, acoustic, and vestibular impulses to the oculomotor nerves(10); (11). Some drawings by Ramön y Cajal from Golgi preparations of the superior colliculus are reproduced, with his captions, in Figure 5.
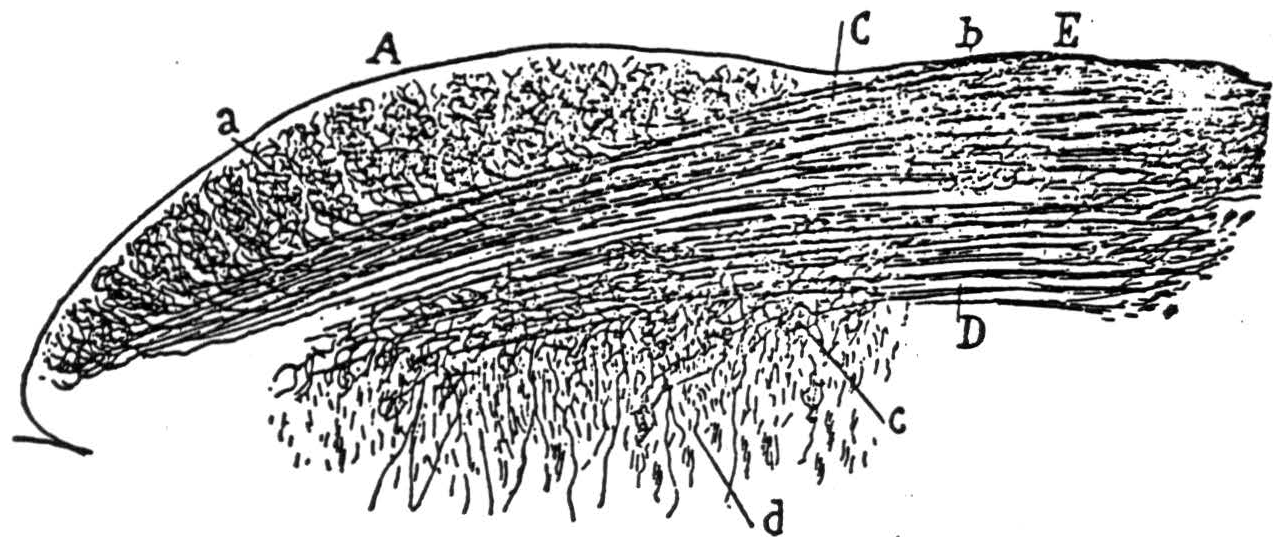
Figure 5b. The following is the original caption. Coupe transversale du tubercule quadrijumeau antérieur; lapin âgé de 8 jours. Méthode de Golgi. A, surface du tubercule tout prës de la ligne mëdiane; B, couche grise superficielle ou couche cendrëe de Tartuferi comprenant les zones des cellules horizontales et des cellules fusiformes verticales; C, couche des fibres optiques; D, couche des fibres transversales ou zone blanc cendré profonde de Tartuferi; L, M, cellules de la couche ganglionnaire ou des fibres transversales; *a, *cellules marginales; b, cellules fusiformes transversales ou horizontales; c, autre cellule de mëme espëce, montrant bien son cylindre-axe; d, petites cellules à bouquet dendritique compliqué; e, cellules fusiformes verticales; f, g, differents types cellulaires de la couche grise superficielle; h, j, cellules fusiformes de la zone des fibres optiques; m, collatérale descendante allant à la substance grise centrale; n, arborisation terminale des fibres optiques.
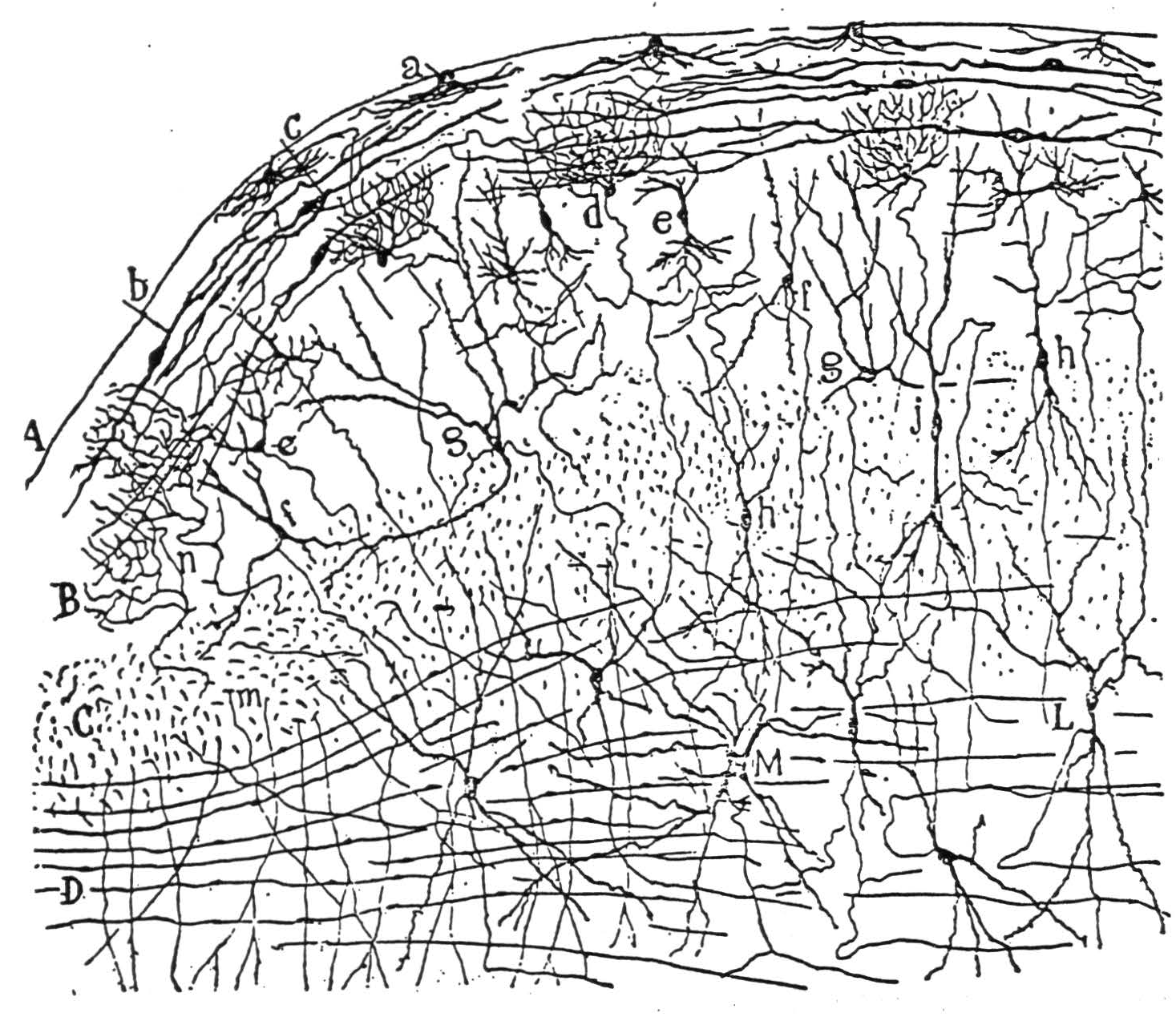
Figure 5a. The following is the original caption. Coupe sagittale montrant l'ensemble des fibres optiques du tubercule quadri-jumeau antërieur; souris âgée de 24 heures. Méthode de Golgi. A, écorce grise du tubercule antérieur; C, courant superficiel des fibres optiques; D, courant profond; E, région postérieure du corps genouillé externe; b, foyer où se terminent des collatérales des fibres optiques; c, nids péricellulaires formés par les fibres optiques; d, fibres transversales de la couche ganglionnaire.
Julia Apter(12); (13), by illuminating small spots on the retina of the cat and finding the tectal point of maximum evoked potential, has demonstrated that each half of the visual field, seen through the nasal half of one eye and the temporal half of the other, maps point-by-point upon the contralateral colliculus. The contours of projection, in angular degrees lateral and vertical from the visual axis, are drawn on the right colliculus as dotted lines in Figure 6. Presumably the calcarine cortex would map similarly, although this has not been tried. In addition, by strychninizing a single point on the collicular surface and flashing a diffuse light on the retina, she obtained change in gaze so as to fix a certain constant point in the visual field. The points for various strychninized places are sketched in solid lines on the right colliculus of Figure 6. It is clear that they nearly coincide with the retinal points which project to the strychninized spot. She showed that if the diffuse light on the retina were replaced by a localized one, the response would occur if, and only if, the points projecting to the strychninized spot were illuminated—apart from certain other smaller effects from the fovea.
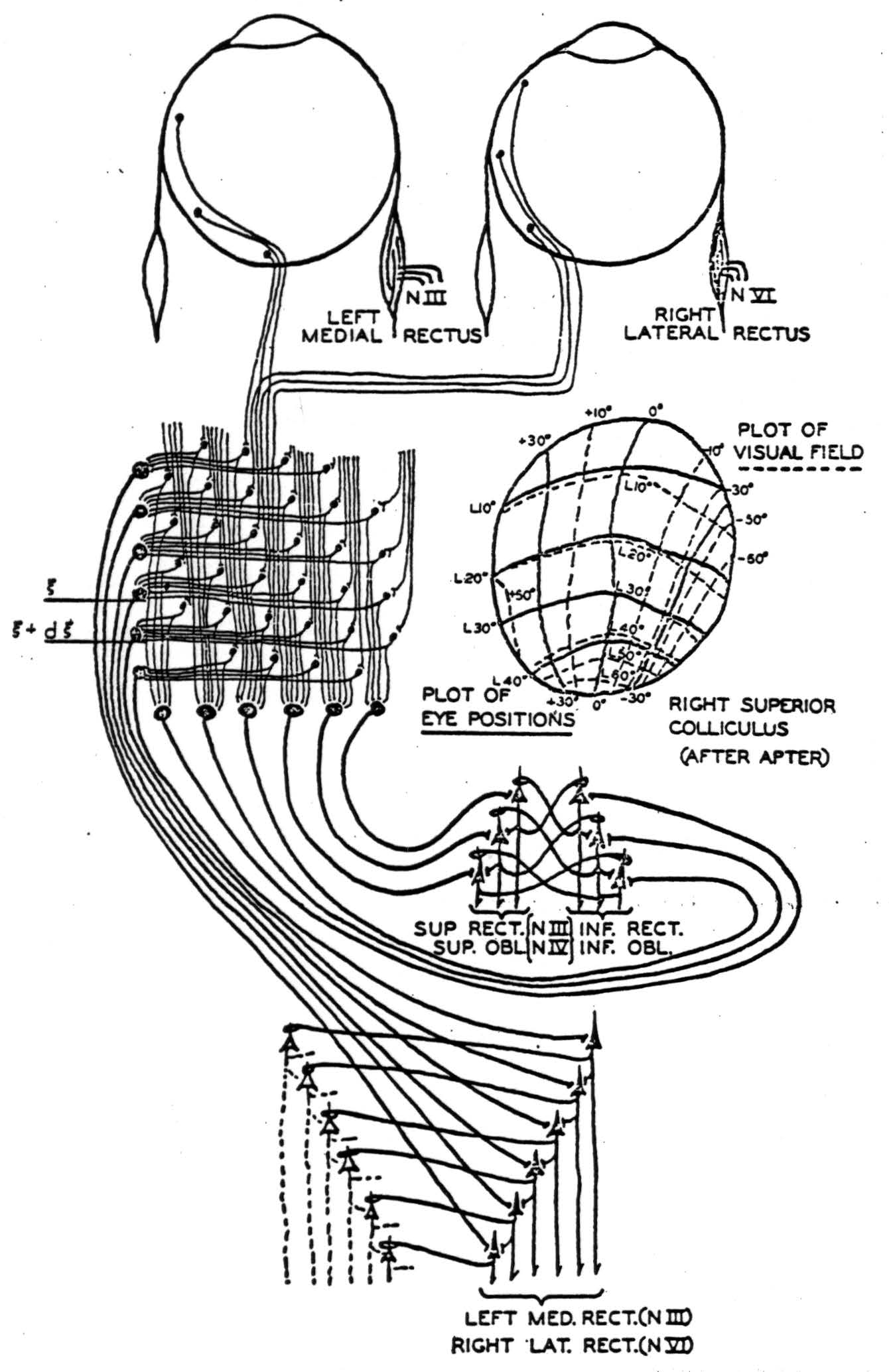
Figure 6. A simplified diagram showing occular afferents to left superior colliculus, where they are integrated anteroposteriorly and laterally and relayed to the motor nuclei of the eyes. A figure of the right superior colliculus mapped for visual and motor response by Apter is inserted. An inhibiting synapse is indicated as a loop about the apical dendrite. The threshold of all cells is taken to be one.
All these results agree well with our initial hypothesis. If x and y are respectively lateral and vertical coordinates in the visual field, and ϕ(x,y) is the brightness inhabiting the point (x, y)—that is, the response of the spot in the optic nerve which images (x, y)— the coordinates x and y of the center of brightness are
where integration is over the whole visual field V. If ξR, ηR are respectively sagittal and lateral coordinates measuring position on the right colliculus CR , and ξL and ηL their mirror images on the left colliculus CL, there will be a mapping
and
To transform equations (4) Into the coordinates of the colliculus will then yield
where
and
are the distributions of brightness on the surface of the colliculus.
Now it clearly makes no difference to the final result whether the true center of gravity (x̄, ȳ) determines the net frequency of impulses sent into the eye-muscles, or whether it is some other pair of numbers u and v that increase monotonically with x and y respectively and vanish with them. For in any case, the eyes must be moved in such a direction as to diminish (u, v), and pari passu (x̄, ȳ); and finally they must remove (u, v), and therefore (x, y), to the origin at the visual axes. Thus, if the two quantities computed from ϕ (x, y) to determine lateral and vertical motion respectively have the form
with a similar integral with ΦR for uL and υL, and any U and V fulfilling the condition that for every η, U (ξ, η) is properly monotonic in η, and for every ξ, V(ξ, η) is properly monotonic in η, then u and v will have the required properties that they shall vanish and vary monotonically with x̄ and ȳ respectively. J. Apter(12); (13) shows that one can write, approximately,
with p(ξ) and q(η) both properly monotonically increasing, neglecting the other variable. This would yield
so that
together with the corresponding expressions for uL and vL involving ΦR, furnish an approximation to (x̄, ȳ). Most general of this type is
where S1 and S2 are non-negative and R1 and R2 are properly monotonic and vanish at the origin. The integration is taken over the range of the collicular coordinates. If S1 = S2 = 1, R1 (ξ) = ξ = R2 (ξ), this is the center of gravity of the afferent excitement upon the colliculi. The simplest schematic way of computing expressions (8) and (9) is actually to carry out the double “integration” on the colliculus, as in Figure 6, so that to compute expression (8) we first add all the afferent impulses within a thin transverse strip, (ξ, ξ + d ξ), to compute
This quantity, for most caudal or greatest ξ, is fed highest into a chain of successively exciting oculomotor neurons; for most anterior, smallest ξ, it comes in lowest. This process provides a net frequency of impulses to the right lateral and medial recti which is certainly weighted by some monotonic factor R1(ξ). Reciprocal inhibition by axonal collaterals from the nuclei of the antagonist eye- muscles, which are excited similarly by the other colliculus, serves to perform the algebraic subtraction to obtain u = uR − uL . The computation of the vertical position v of the quasi-center of gravity is done similarly. It is also possible, in whole or in part, that the difference ΦL(ξ, η) − ΦR (ξ, η) in equation (8), or the sum Φ*L* (ξ, η) + ΦR (ξ, η) in (9), is computed by commissural fibers running between contralateral tectal points with the same coordinates, instead of in the oculomotor nuclei.
We have omitted to divide the final results u and v by the total luminous flux before calling (u, v) the “quasicenter of gravity.” For the reflex this makes no difference, since (u, v) finally lies at the origin, which does not change on multiplication by A. Similarly, Apter's single-point strychninizations are not relevant to the question. But if several distinct points are strychninized on the colliculus at once, then equation (8) requires gaze to deviate by a lateral distance which is the sum of the deviations evoked from the points separately. This may happen; but it seems more likely that the total excitation from the colliculus is in fact kept constant by compensatory variations in the background of facilitation or inhibition, produced perhaps by reverberation with the periaqueductal grey, if not internally in the tectum. H. Klüver's observation(14) should be recalled here, that even decorticate monkeys whose corpora quadrigemina are not otherwise deafferented detect and discriminate total luminous flux.
But if the colliculus takes a “weighted center of gravity” of an impingent distribution of light, in our most general sense, for suitably chosen partially monotonic positive functions U(ξ, η), V(ξ, η)*, *so dividing it by the total luminous flux, then, and only then, by a theorem of Reisz, whenever a finite (or infinite) number of points of the colliculus are simultaneously strychninized, the consequent gaze will lie within the smallest convex polygon (or simplex) containing all the points whose projections are strychninized.
This example may be straightforwardly generalized to provide a uniform principle of design for reflex-mechanisms which secure invariance under an arbitrary group G. In some way, out of the whole series of transforms Tϕ of an apparition, one of them ϕ0 is elected to be standard—e.g., one of a standard overall size—and when presented with ϕ, the mechanism computes one or more suitable parameters a(ϕ), b(ϕ), …, which define its position within the series of Tϕ's in a univocal way so that their simultaneous equality a (ϕ) =a(S ϕ), , b(ϕ)=b(S ϕ) etc., is sufficient to entail S = I, the identity. The errors
if they do not already all vanish, then impel the mechanism to perform a suitable operation Tϕ so determined as to diminish the parameters E(Tϕ) as compared to E(ϕ). This process may be repeated many times, reducing the E (ϕ) at every stage, until the E(ϕ)'s all vanish and ϕ = ϕ0, its standard. The mechanism is circular: it follows the scheme
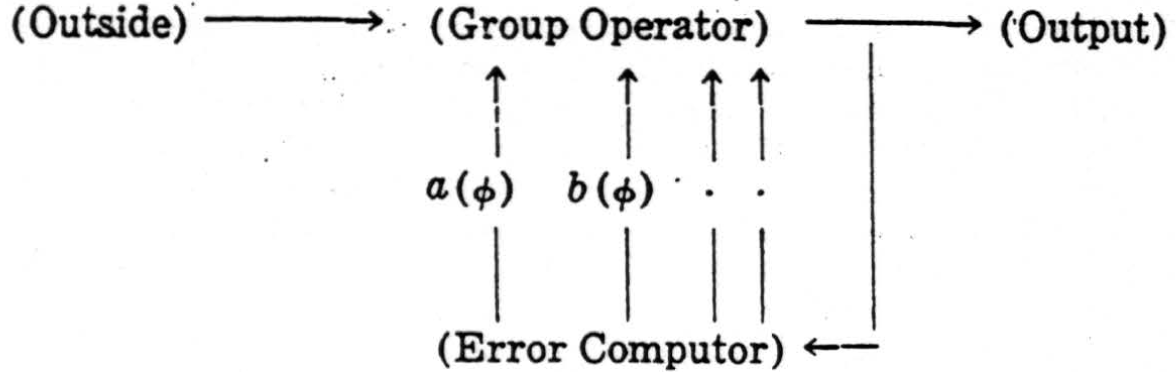
In the case of the colliculus, the group is the two-dimensional translation-group, and the two quantities a(ϕ) and b(ϕ) are the coordinates of the “weighted center of gravity” of equation (6). For any general group of the type we are considering, quantities a(ϕ) of this type may always be found, as is shown in the theory of the irreducible representations of the group G .
We have focused our attention on particular hypothetical mechanisms in order to reach explicit notions about them which guide both histological studies and experiment. If mistaken, they still present the possible kinds of hypothetical mechanisms and the general character of circuits which recognize universals, and give practical methods for their design. These procedures are a systematic development of the conception of reverberating neuronal chains, which themselves, in preserving the sequence of events while forgetting their time of happening, are abstracted universals of a kind. Our circuits extend the abstraction to a wide realm of properties. By systematic use of the principle of the exchangeability of time and space, we have enlarged the realm enormously. The adaptability of our methods to unusual forms of input is matched by the equally unusual form of their invariant output, which will rarely resemble the thing it means any closer than a man's name does his face.
Footnotes
Acknowledgements
The authors wish to express their great indebtedness to Professor Elizabeth Crosby for her generous assistance and more especially for permission to quote her as yet unpublished observations.
This work was aided by grants from the Josiah Macy, Jr. Foundation and the Rockefeller Foundation.
Literature
Ramón y Cajal, S. 1911 Histologie du Systeme Nerveux. Paris: Maloine.
Lorente de Nó, R. 1922. “La Corteza Cerebral del Raton.” Trab. Lab. Invest. Biol. Univ. Madr., 20, 41-78.
O'Leary, J. L., and G. H. Bishop. 1941. “The Optically Excitable Cortex of the Rabbit.” J. Comp. Neur., 68, 423-478.
Zunino, G. 1909. “Die Myeloarchitektonische Differenzierung der Grosshirnrinde beim Kaninchen.” J. Psych. u. Neur., 14, 38-70.
Barris, R. W., W. B. Ingram, and S. W. Ranson. 1935. “Optic Connections of the Diencephalon and Midbrain in Cat.” J. Comp. Neur., 62, 117-144,
Dempsey, E. W., and R. S. Morison. 1943. “The Electrical Action of a Thalamocortical Relay System.” Amer. Jour, of Physiology, 138, 2, 283-296.
Ramón y Cajal, S. 1900. Die Sehrinde. Leipzig: Barth.
Ariens-Kappers, C. V., G. C. Huber, and E. C. Crosby. 1936. The Comparative Anatomy of the Nervous System of Vertebrates. New York: The Macmillan Co.
Ward, A. A. and H. L. Reed. 1946. “Mechanism of Pupillary Dilatation Elicited Cortical Stimulation.” J. Neurophysiol., 9, 329-336.
Brouwer, B. 1917. “Klinisch-Anatomische Onderzoekingen Over de Oculomotoriuskern.” Voordracht, Gehouden in de Vergadering der Amsterdamsche Neurologenvereeniging op 7 December 1916, in het Binnen-Gasthuis, Collegekammer voor Neurologie. Neder. Tijdschrift voor Geneeskunde, Eerste Helft, 14, 1-11.
Lorente de Nó, R. 1933. “The Vestibulo-Ocular Reflex Arc.” Arch. Neurol, and Psychiat., 30, 245-291.
Apter, J. 1945. “The Projection of the Retina on the Superior Colliculus of Cats.” J. Neurophysiol., 8, 123-134.
Apter, J. 1946. “Eye Movements Following Strychninization of the Superior Colliculus of Cats.” J. Neurophysiol., 9, 73-85.
Klüver, H. 1942. “Functional Significance of the Geniculo-Striate System.” Visual Mechanisms, Pennsylvania: J. Cattell Press, 253-299.
Huber, G. C., E. C. Crosby, R. T. Woodburne, L. A. Gillilan, J. O. Brown, and B. Tamthai. 1943. “The Mammalian Midbrain and Isthmus Regions. I. The Nuclear Pattern.” J. Comp. Neur., 78, 129-534.
Morison, R. S., and E. W. Dempsey. 1942. “The Production of Rhythmically Recurrent Cortical Potentials After Localized Thalamic Stimulation.” Amer. Jour. of Physiol., 135, 293-300.
Morison, R. S., and E. W. Dempsey. 1943. “Mechanism of Thalamo-Cortical Augmentation and Repetition.” Amer. Jour. of Physiol., 138, 297-308.
Woodburne, K. T., E. C. Crosby and R. E. McCotter. 1946. “The Mammalian Midbrain and Isthmus Region. II. The Fibre Connections.” J. Comp. Neur., 85, 67-92.
Epi-search analysis
Word cloud: Afferents, Apparition, Area, Auditory, Axons, Cells, Cellules, Center, Colliculus, Compute, Coordinates, Cortex, Cortical, Crosby, Dimensions, Distribution, Eta, Excitation, Eyes, Fibers, Fibres, Figure, Following, Form, Functions, General, Gravity, Group, Impulses, Invariants, Lateral, Layer, Manifold, Mechanism, Net, Neurons, Nuclei, Original, Partial, Point, Position, Project, Square, Superior, Surface, Transformations, Upper, Value, Vertical, Visual
Topics: Cortex, Colliculus, Visual
Keywords:
Mechanisms, Project, Forms, Cortex, Transformations, Universals, Mechanism, Area, Lobe, Excitation (final)
Cortex, Fibers, Layer, Neurons, Nuclei, Axons, Fibres, Cells, Neuron, Manifold (full text 1)
Mechanisms, Project, Forms, Cortex, Transformations, Universals, Mechanism, Area, Lobe, Excitation (full text2)
Citations:
Related Articles:
Related books:
Keywords from the citations and related material: Cortex, Brain, Mechanisms, Coding, Neuroscience, Pathways, Headache, Function, Cells, Processing.