Robust policy analysis for complex open systems

Steven Bankes
Evolving Logic, USA

Abstract

Real institutions are ‘open’, which can result in unpredictable changes in both their internal resources and external environment. This implies that a broadly useful approach to decision support must not rely on either prediction or on gathering all relevant information before useful calculations can be made. This paper describes an approach to highly interactive decision support based upon using ensembles of alternative models, robust option analysis, and adaptive strategies.

Open systems

Real institutions are ‘open’ in at least two senses. First, their environment is open, and they face, to a greater or lesser degree, the possibility of changes that cannot be predicted or forecast in any detail. Second, our institutions are composed of individuals whose identity changes over time as new members join, and others depart. These individuals each have their own background, skills, social networks, and goals. Seldom do the goals of all members of an organization completely align, and even when they do, their perceptions and judgements will not. As the interests and beliefs of the members of an institution cannot be uniquely aggregated, the behavior of institutions and organizations cannot be fully explained by the maximization of a single utility function, nor by any single representation of beliefs. Politics is inevitable, and an effective decision support infrastructure must conform to the openness of both the external environment of an institution, and its internal processes.

This situation contrasts markedly with the assumptions that are required to use the most powerful tools in the decision analyst’s toolkit. ‘Classical’ approaches to decision support depend upon a portfolio of tools that have been drawn from a variety of disciplines, including Game Theory, Economics, Statistical Decision theory, Artificial Intelligence, and Operations Research. Many of these tools are rigorous and sophisticated, and have proven their value on a host of problems spanning several decades of research. But, essentially all of the most powerful mathematical frameworks require explicit bounding of the problem, specification of a model of the system that captures all our knowledge about it, and a single value function that defines what a good solution to the problem looks like. In contrast, the problems of open systems are ‘deeply uncertain’. That is to say, one or more of these requirements cannot be met. The pragmatics of the problems faced by open systems makes the use of our best tools problematic or even counter-productive. This conflict between the requirements of the tools in our analytic toolbox and the pragmatics of many real world decisions explains the striking market failure of decision support as a technology over the past many decades.

As a consequence of the open boundaries of the problems real institutions face, there are very strong limits on our ability to predict the consequences that will result from any given action. As a consequence, any method based on forecasting the future will have significant problems and limitations in dealing with problems where surprise is very likely. Organizations that must contend with open environments will typically be highly adaptive, in order to be robust in the face of unpredictable future circumstances. To treat organizations as mechanisms that can be engineered for greatest efficiency is to risk making the client organization more vulnerable to surprise. A successful decision support system must integrate with the adaptive processes of its host institution in such a way that the adaptive capacity is enhanced, not reduced. The greatest failures of decision support systems can be understood as a consequence of sacrificing adaptive capacity for the sake of enhanced efficiency and rationality. In fact, inefficiency and irrationality can be purposeful, if they serve the needs of adaptation and hence robustness.

As a consequence of the fact that organizations typically also have open boundaries, there will often be strong pragmatic limits to capturing organizational goals as consensus value functions, and to capturing organizational knowledge as consensus models or probability distributions. This fact strongly limits the utility of methods that require the definition of value functions, system models, and a priori probability distributions as starting points.

Exploratory modeling and robust decision methods

Decision and policy analysis for open systems can benefit from all the traditional analytic tools and methods, but if they are to bring significant value, they must be used in a way that addresses the problems described above. In this paper, I will describe one approach to providing this needed context, which combines the insights of exploratory modeling (Bankes, 1993, 2002) and robust decision methods (Bankes & Lempert, 1996; Lempert, et al., 2002; Lempert, et al., 2003).

This approach can be motivated by four assumptions that synopsize the foregoing discussion of open systems:

1. Our knowledge of the problem cannot be uniquely characterized;
2. Success depends upon satisfactory performance in spite of an uncertain future;
3. All plans are adaptive;
4. All planning is iterative.

Corresponding to these four assumptions are four design goals for the decision support systems we build:

1. Aggressive use of ensembles of alternatives, including ensembles of models, ensembles of scenarios, ensembles of decision options, and ensembles of probability distributions;
2. Options analysis based on the concept of robustness rather than optimality;
3. Support for representing, testing, and discovering adaptive strategies;
4. Highly interactive user interfaces allowing for integration of human judgement and machine calculation supporting iterative planning methods.

Software embodying these design goals (Computer Assisted Reasoning system: CARs) has now been utilized for decision problems for major manufacturers, defense planning, counter-terrorism, and a variety of public policy applications. For illustrative purposes, the following example will be used to illustrate these various aspects of our approach, and to provide a unifying story. The CARs technology has to date been used in six different applications for the automotive industry. The first of these, and the simplest, provides a powerful example of the challenges of open systems, and how the techniques described here can be used to meet these challenges.

In this application, a major automotive manufacturer was facing a decision between a series of candidate product offerings. This choice involved a billion dollar investment, committing the firm to a product offering that would extend over years, and was potentially a ‘bet the company’ decision. It was one that was proving very difficult to make. Figure 1 shows a typical graph that might be used to compare options such as the six programs compared here (note that the program names and other details have been modified to avoid disclosing any proprietary information). While this graph shows Program 2 to be the optimal choice, it amounts to a forecast of market outcomes over the coming 7-12 years, and thus is conditioned on a variety of assumptions about everything from consumer taste to technology performance to currency exchange rates to the price of oil. Thus, this sort of analysis was not compelling for parties to the decision with different opinions about what the future might hold, it was very easy to come up with plausible scenarios where other candidates would be superior choices. The champions of the various candidates had divergent beliefs about

Figure 1 Internal return on investment for six programs for nominal assumptions

the future, usually communicated via a story that carried a heuristic argument (e.g., “we must boldly innovate or we will be left behind” vs. “we have built valuable brand recognition and must not damage it by creating a product that clashes with consumer expectations”). So, the competition between choices, while influenced by technical inputs from engineering and marketing departments was highly political. This is a common situation in large organizations.

The classical solution recommended by decision theory for the problem of an uncertain future is to weight the universe of assumptions with probabilities, and to then make the choice based on expected outcome. That was not applied in this situation (and is usually never applied to the really important problems) because the future the company faces is deeply uncertain. Import individuals in the company hold very different beliefs about the future, and means are needed to create consensus, which a mechanical solution calculator will not provide. Further, the elicitation of a highly dimensioned probability density function is a pragmatic impossibility here, and should that elicitation be attempted, the inputs will likely be gamed as participants try to bias the mathematical machinery (consciously or unconsciously) so that it will produce the ‘correct’ result. This automobile company is an open system confronting a potentially surprising future. The uncertainty it must contend with is deep, and the techniques of probabilistic decision theory will not directly provide a solution.

Ensembles of alternatives

For closed systems such as those associated with engineering design, problem definition can be captured in single consensus models, single prior probability distributions, and single cost or value functions. For open systems, we find it useful to explicitly represent large or infinite ensembles of alternatives. The CARs software supports reasoning over ensembles of models, projecting ensembles of plausible futures, assessing these outcomes with ensembles of metrics, in order to assess the properties of ensembles of plans. The representation of ensembles is accomplished by a combination of databases containing a finite collection of individuals, and generative representation where any member of a potentially infinite ensemble can be produced on demand. The latter technique requires devising a data structure that indexes the ensemble. Arbitrary members of the ensemble can then be created by means of a generator that maps from index data structures to ensemble members. Reasoning over such a virtual ensemble has an inductive character, as assertions about the properties of the entire ensemble must be based on the properties of a finite sample of cases.

A particularly powerful use of the ensemble machinery is to support reasoning over ensembles of models. By allowing the knowledge base of system properties to be represented by an ensemble of both alternative and complementary models, explicit room is made for competing points of view among different stakeholders, and for diverse sources of knowledge that may most easily represented in differing model frameworks.

For the automotive example described above, we were able to use models obtained from technical groups working on consumer demand, industrial capacity, financial return, and other sub-problems and from them fashion a scenario generator. The scenario generator takes as input a long list of assumptions about factors such as the cost of production, consumer demand, competitor behavior, interest and exchange rates, and produces in response a scenario. Such a scenario is a picture or a story of the future of the company contingent on the assumptions and decisions that lead to it. As we are using the ‘model’ here to generate scenarios with no intent to predict, we are able to use wide ranges of functional forms or parameter estimates for phenomena that are poorly understood. And if the scenario generator can generate all scenarios that are important to the decision at hand, it can be used as a basis for option analysis, without the necessity of prediction or forecasting. As will be described below, for decision analysis we will typically use a scenario generator as a challenge generator (and the ensemble of futures it represents as a challenge set), and we can then seek decisions robust to these challenges. Figures 2 and 3 show policy landscapes created by visualizing the outcome of one or more options across a range of alternative futures. Figure 2 presents the outcome of one of the programs across a range of assumptions about two of the most influential uncertainties, the cost of production and the overall demand for the company’s products. Figure 3 shows the impact of one of these uncertainties for all six programs. These landscapes can be thought of as slices through a multi-dimensional ensemble of possible futures. The most interesting of these views will show both hopeful scenarios and those where a given choice would have poor results.

Visualizations such as these present only a restricted subset of the possible outcomes that could result from any given decision. They are a thin slice through a multi-dimensional space of possible futures. To support conclusions about properties of the entire ensemble, this sort of visualization must be augmented by additional features. In our work we have used three types of methods to do this:

1. The software provides interactive controls allowing the user to manually look for views that contradict a pattern of outcome that suggests a hypothesis about ensemble properties;
2. Search methods can be used to seek important cases (often counter-examples) to produce versions of a visualization that are particularly interesting;
3. Derived measures that synopsize the pattern of outcome of across multiple dimensions can be used to collapse the dimensionality of the ensemble, making it easier to grasp.

Robustness

As Herb Simon observed long ago (Simon, 1959), decision makers do not optimize, they satisfice. But they do more than that. They seek alternatives that are insensitive to the uncertainties they cannot escape. The palate of the decision makers art, including techniques such as temporizing, incremental action, institutional design, and even bold actions that ‘invent the future’, are all means to escape the problem of unpredictability by finding choices that they believe will not cause

Policy landscape

Figure 2 Internal rate of return vs. cost of production and total volume

Figure 3 Policy landscape - Net present value vs. total volume and program chosen

them regret, no matter how the uncertainties turn out. In order for our decision support systems to engage decision makers in terms that make sense to them, they must operate not to calculate optimal decisions under specific assumptions, but rather to illuminate the failure modes of candidate actions, and assist in the discovery of options that have few failure modes. That is to say, decision support systems should help discover robust options that will perform satisfactorily across the widest range of plausible assumptions. A challenge set (either explicit or virtual) can be a useful tool for testing for robustness. It can serve as the domain for a search process seeking failure modes. Interactive visualizations that reveal the pattern of scenarios that spell success or failure to a candidate strategy can be a powerful means for users to deepen their understanding of their options and can provide a basis for crafting new options that combine the strengths of two or more existing candidates.

Very difficult scenarios may cause problems for any strategy, so in determining the failure modes of strategies, it can be helpful to use a measure of the relative performance of strategies, such as ‘regret’. Regret is the difference between the performance of a given strategy in a particular scenario and that of the optimal strategy for that scenario. Following Savage, (1950), the regret of strategy j in future f using values m is given as

where strategy j' indexes through all strategies in a search to determine the one best suited to the conditions presented by future f.

Six regret landscapes for the competing programs in the automotive example are displayed in Figures 4-9, one for each program. These landscapes are green only where that choice is the best of the six, other colors (refer to online version of paper) reflect how much worse than the optimal strategy that choice would be. While none of these choices dominates across the space, it is apparent that this sort of visualization can give the user the opportunity to quickly identify the strengths and weaknesses of each candidate, which is not possible with the earlier visualizations.

Adaptive planning

Adaptation is perhaps the most powerful means to cope with the uncertainty associated with open systems. However, knowing this fact alone does not help the decision maker determine how to adapt, or provide any guidance to the analyst in constructing good adaptive options. At present, analytic methods lay out static strategic choices, and the adaptation in real organizations is mostly the result of human heuristic reasoning. Automated help in devising well crafted adaptive strategies could provide significant improvements in the performance of many organizations, but at present no tools are available to do this.

Our approach to this problem is to provide users with a facility to create new options by combining existing candidates through various adaptive mechanisms. Examples of useful mechanisms include decision trees with explicit signposts or threshold values that will trigger action, continuous adjustment mechanisms drawn from, for example, control theory, and portfolios that provide collections of levers hedging against a variety of future circumstances. Thus, the user might choose to create a hybrid of two of the programs shown in Figure 3 in an attempt to combine their strengths and compensate for their weaknesses.

This revision of the set of choices can be done recursively, with the ensemble of policy options changing over time as the user learns more about the problem. This process can be initialized with a collection of primitive actions we call ‘levers’. These are simple actions the organization has the potential to select. These fundamental actions can be assessed for robustness, and if failure modes are discovered they can then be combined into more complex and more adaptive strategies. Iterating through this process, various adaptive mechanisms can be recursively applied to the increasingly sophisticated ensemble of possible actions until the process finally provides choices of sufficient adaptive complexity to meet the challenge of a changing environment.

Interactive decision support

Important decisions can be informed by both by data residing in computers and knowledge residing in people. Decision methods that require all relevant human data to first be made explicit before calculations can begin create a very large barrier to the utilization of knowledge. Iterative planning methods can improve on this situation by allowing the results of the nth iteration to provide context for eliciting new knowledge from humans as input to the (n+1)^th. Thus, decision support software designed to support rich options for interactivity can serve to help merge information resources of the computer and human parts of the system. Interestingly, such software can also serve as a bridge to enhance communication among an organization’s staff.

This use of decision software as a backdrop to productive conversations was observed during the automotive application described here. The contest between the various program options was partially the consequence of divergent conversations among

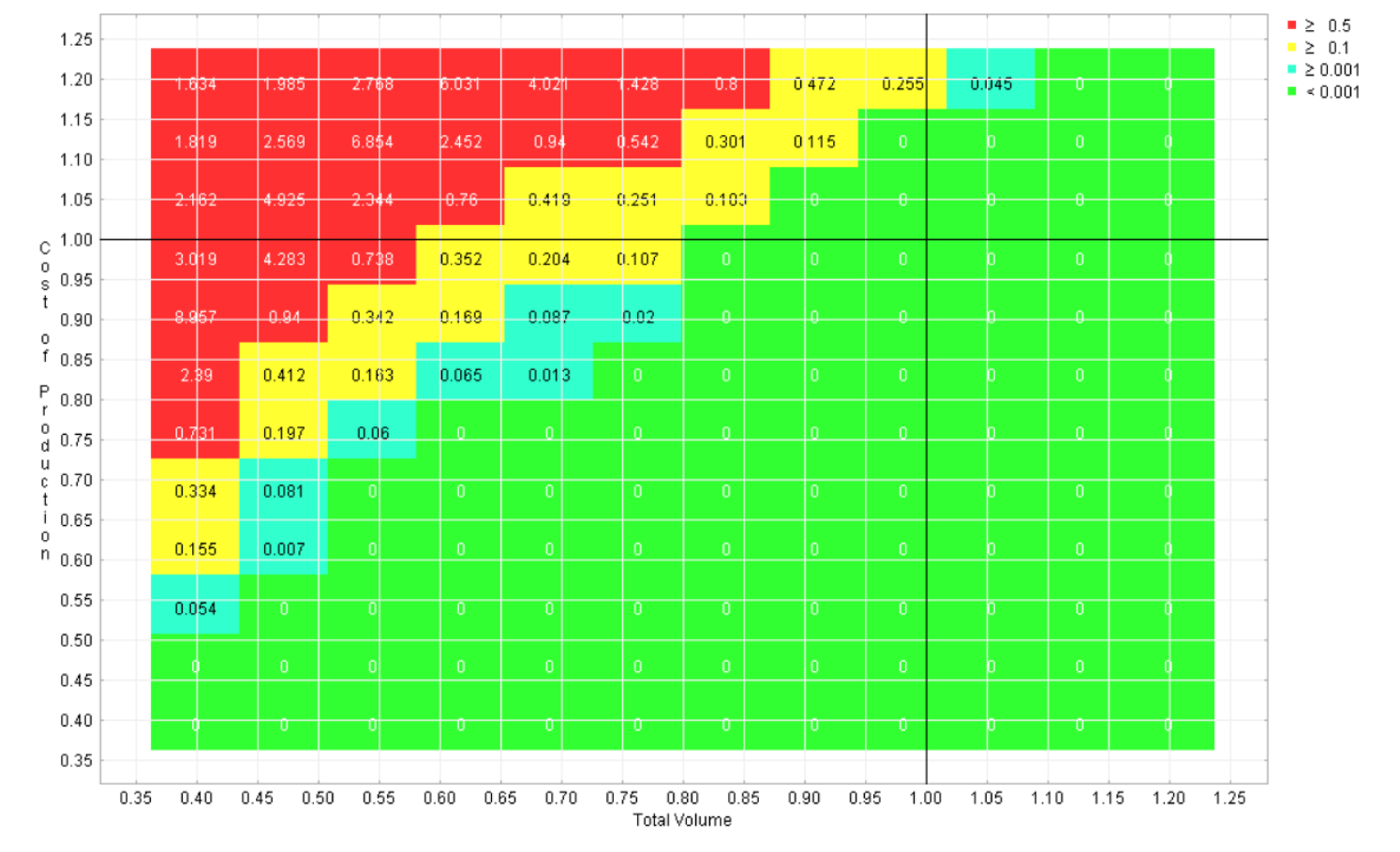
Figure 4 Regret landscape for program 1

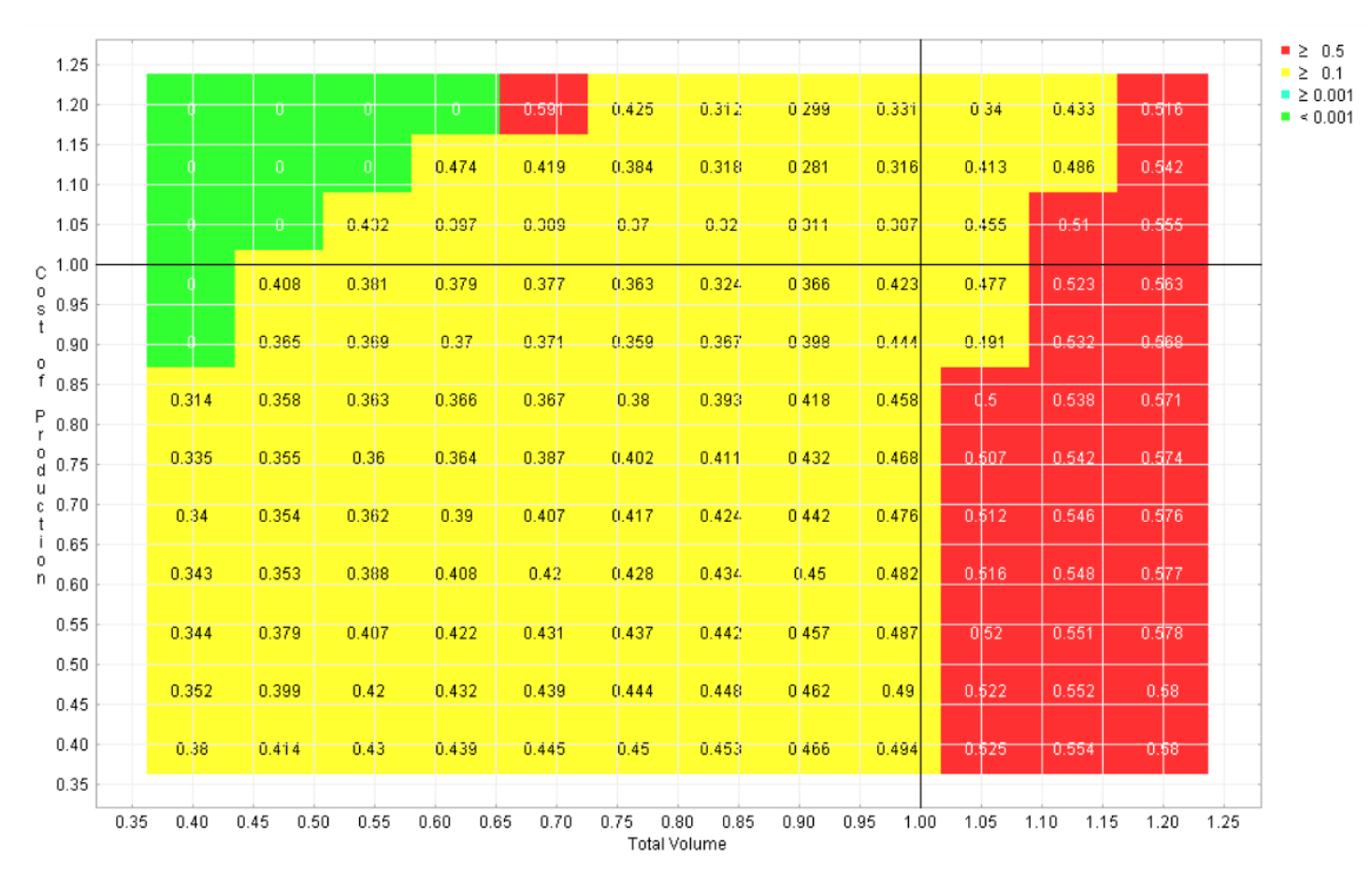
Figure 5 Regret landscape for program 2

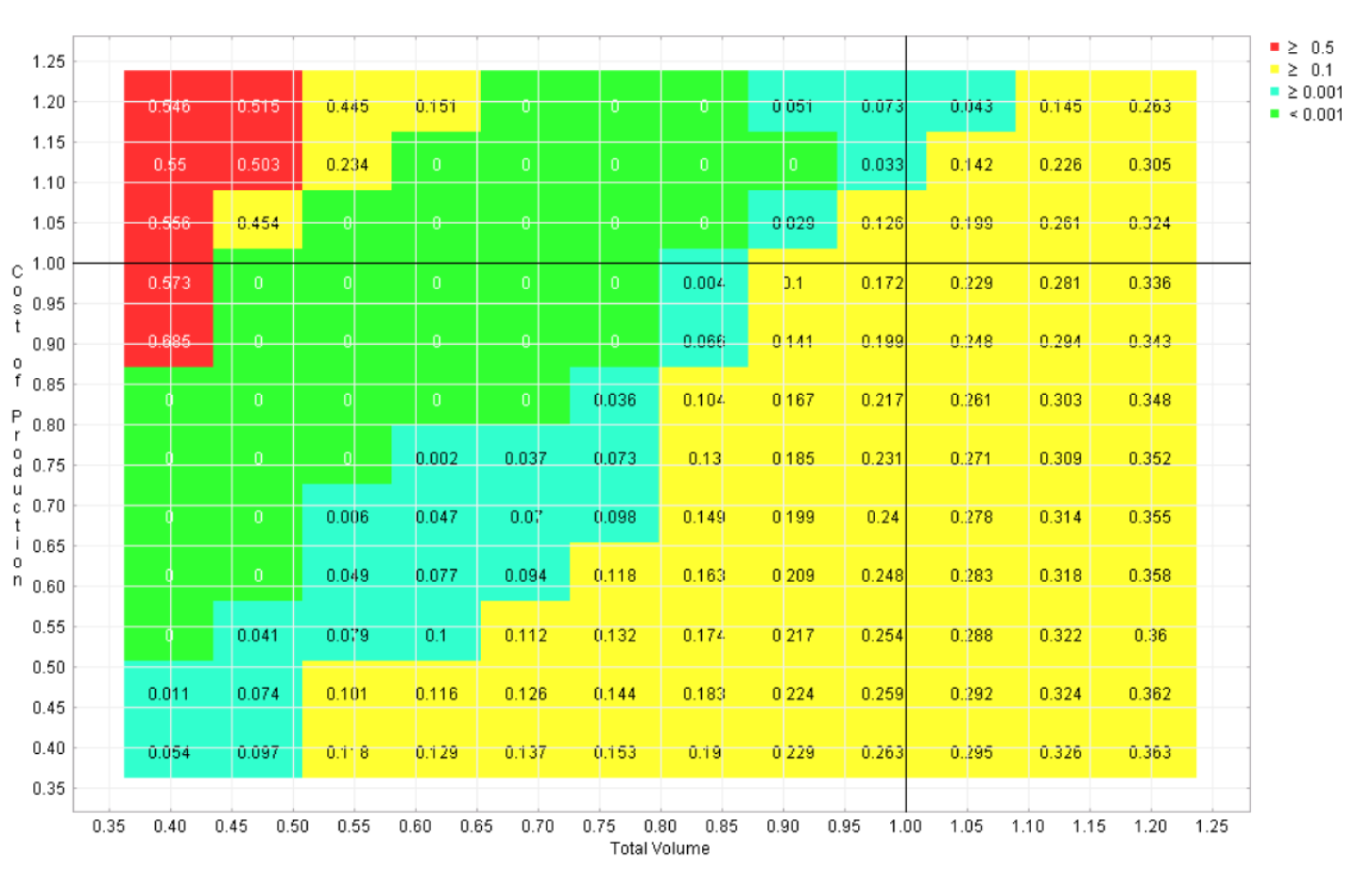
Figure 6 Regret landscape for program 3

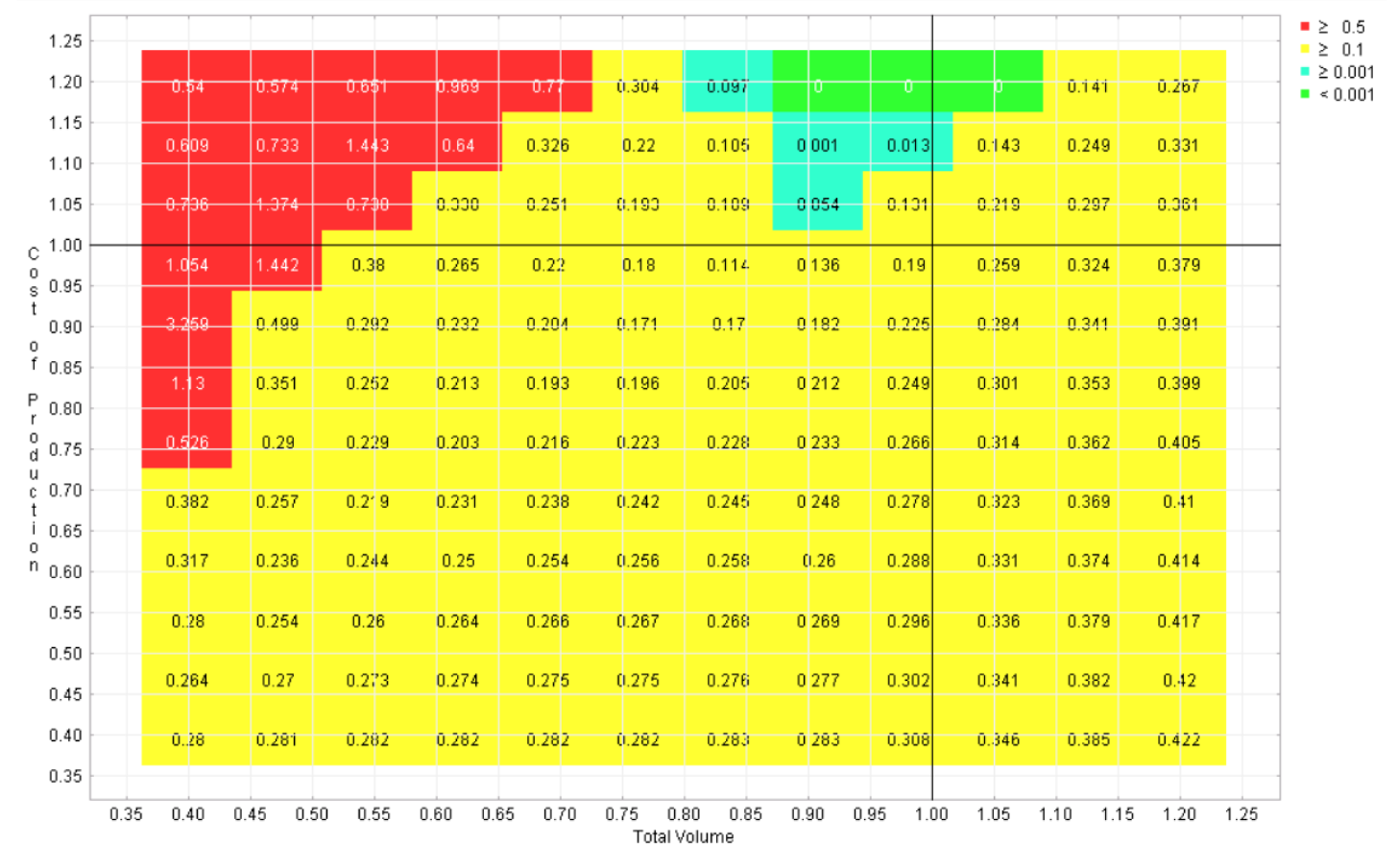
Figure 7 Regret landscape for program 4

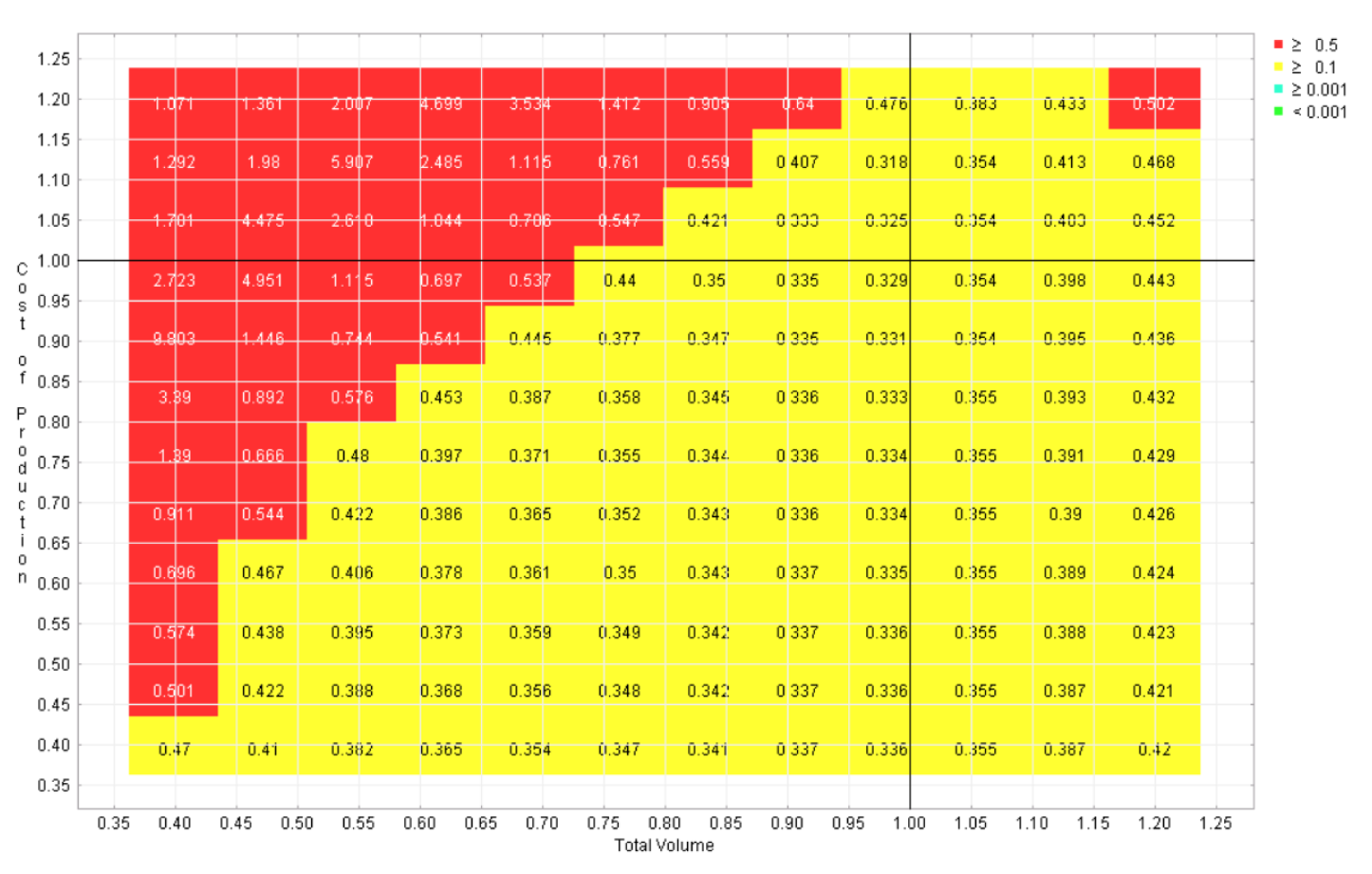
Figure 8 Regret landscape for program 5

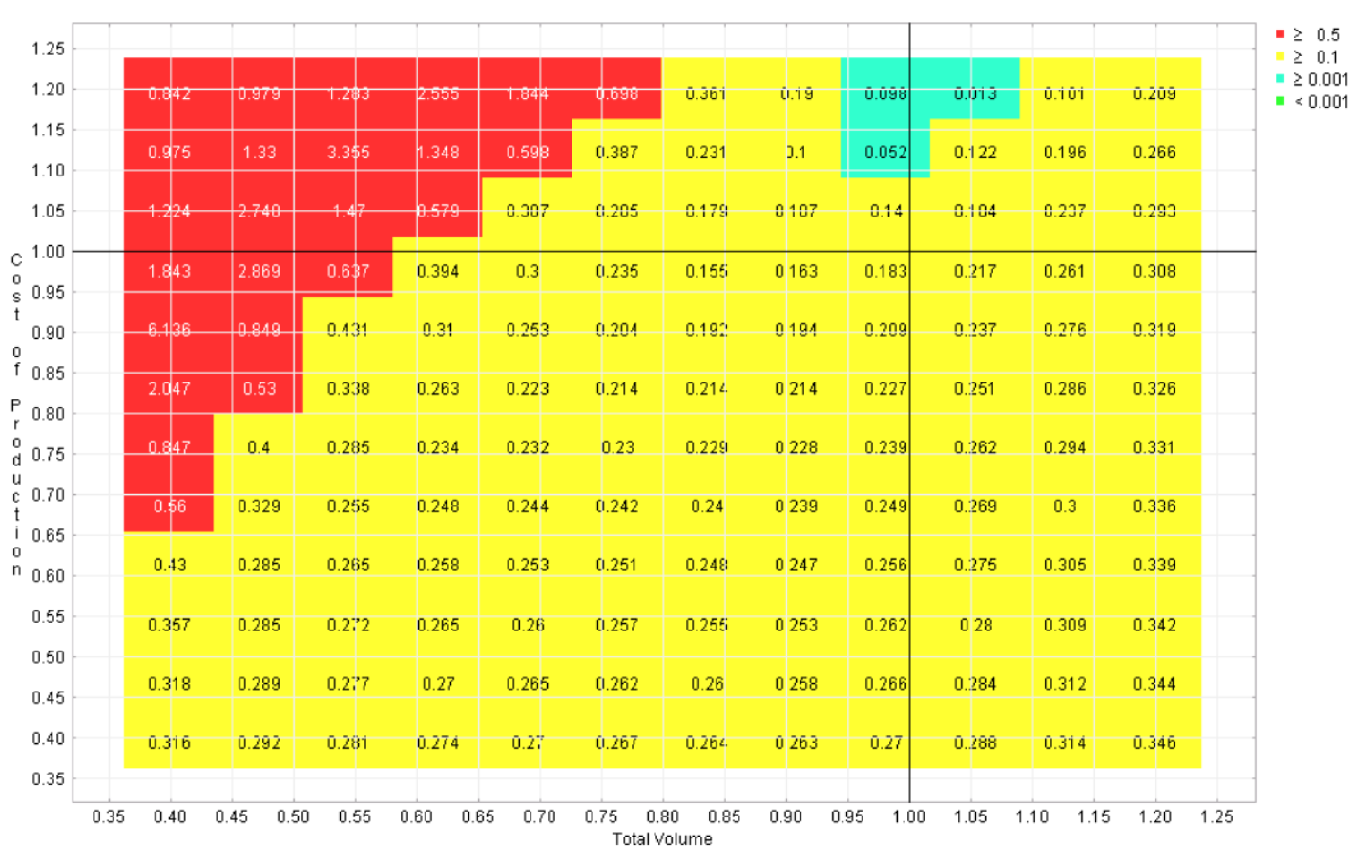
Figure 9 Regret landscape for program 6

staff from very different backgrounds. The concerns, language, and spreadsheets of engineering, marketing, and financial departments were not readily combined. As described above, shifting from forecasting to scenario generation allowed us to combine what otherwise were separate models. Further, once the visualizations of Figures 4-9 were available, productive conversations between different groups were seen to occur with the visualizations as a backdrop. “You see that red region just to the pessimistic side of the nominal case? That’s what I’ve been talking about. I think that possibility should worry us very much. That’s why I don’t think option #1 is a good idea.”

The use of computers to predict the future can be very powerful when the predictions can be relied upon. This situation seldom applies to the most important decisions made in large organizations. They are typically dealing with deeply uncertain open systems. For these problems, the computer can provide more useful assistance by entering the conversation among the parties to the decision as an arbiter of the conversation. Decisions can be strongly facilitated by calculations that reveal previously unforeseen dangers or demonstrate that certain worries are misplaced. And by helping communities to better understand the potential implications of alternative choices, the basis for decision can be clarified.

Co-evolution of plans and challenge scenarios

The four elements described above can be combined to produce a wide variety of decision methods, and these in turn used as a basis for specific decision support systems. In recent work, my group has focused on the use of a coevolutionary dynamic where ensemble representations of both challenge set and choice set evolve in parallel, producing progressively more robust decision options and progressively more difficult challenge sets. (For a detailed example of this approach see Lempert et al., 2003.)

In the automotive example, this approach would work as follows. First, existing models, data, projections, and opinion are drawn upon to create an initial ‘challenge set’ of alternative views of the problem any candidate decision must contend with. An initial ensemble of possible decisions is similarly defined. For example, the six program options and the range of possible values for cost of production and volume shown in Figure 2 could serve as initial decision and challenge sets. The computational infrastructure (CARs) supports the generation of scenarios that combine one member from each set, and search or sampling processes across these choices can be launched to provide information about the choices that do well with particular challenges and the challenges that serve as worst cases for particular decisions. This information can be summarized to characterize the robustness properties of the decisions being considered as seen in Figures 4-9.

With this starting point both ensembles, the challenge set and the choice set, are made to evolve over time, with changes imposed by a combination of new external data, human judgement, and computation. This (co)evolution is driven by the fundamental competition between the challenges and the choices. Should a choice be discovered that is adequate for all challenges that have been tested, new challenges are sought that are more stressing to that tentative decision. Automated search algorithms can seek to discover new challenges that will added to the challenge set. The environment or external data bases can be scanned for data leading to challenging new scenarios. Human creativity can be tapped to conceive plausible challenges that would cause the tentative decision to fail. If needed, new dimensions of uncertainty that come to light through this process can be added to the scenario generator.

Conversely, if no member of the current choice set can be found to meet all challenges, means are employed to enrich the choice set. For example, the identification of the leading candidates and their failure modes (as in Figures 4-9) can serve as inputs to processes that add adaptive complexity to the space of possible decisions. This enhancement of the choice set can be accomplished either through automated suggestion or human action. For example, if two leading candidates are complementary, each of them succeeding in scenarios where the other fails, they can be used to create a compound strategy that switches between the two as the details of the actual situation unfolds. Thus, if data can be identified that will become available in the future and can distinguish the nature of the challenge, a branched adaptive strategy that monitors the environment and switches between component strategies based upon observation might be added to the choice set.

This process can continue indefinitely, modifying the choice set to produce increasingly adaptive strategies, while in parallel modifying the challenge set by adding scenarios designed to break the leading candidates. Both humans and computers can contribute to this process, and by virtue of the resulting evolutionary arms race, there is a potential to discover strategies that can be robust to a very wide range of possible future scenarios.

No strategy, no matter how adaptive, can be guaranteed to be immune to all surprises the Universe might throw at us. But, the approach described here allows us to utilize both human and machine resources to produce the most robust strategies possible given our resources. This can be a helpful approach in meeting the problems posed by complex open systems.

References

Bankes, S. (1993). “Exploratory modeling for policy analysis,” Operations Research, ISSN 0030364X, 41(3): 435-449.

Bankes, S. (2002). “Tools and techniques for developing policies for complex and uncertain systems,” Proceedings of the National Academy of Sciences, ISSN 00278424, 99: 7263-7266.

Bankes, S. and Lempert, R. J. (1996). “Adaptive strategies for abating climate change: An example of policy analysis for complex adaptive systems,” in L. J. Fogel, P. J. Angeline, and T. Back (eds.), Evolutionary programming V: Proceedings of the fifth annual conference on evolutionary programming, Cambridge, MA: MIT Press, pp. 17-25, ISBN 0262061902.

Lempert, R. J., Popper, S. W. and Bankes, S.C. (2003). Shaping the next one hundred years: New methods for quantitative long-term policy analysis, RAND MR-1626-RPC.

Lempert, R. J., Popper, S. W. and Bankes, S.C. (2002). “Confronting surprise,” Social Science Computing Review, ISSN 08944393, 20(4): 420-440.

Savage, L. J. (1950). The foundations of statistics, New York, NY: Wiley, ISBN 0486623491.

Simon, H. (1959). “Theories of decision-making in economic and behavioral science,” American Economic Review, ISSN 00028282, 49(1): 253-283.