Ethical implications of the laws of pattern abundance distribution
Stephan R. P. Halloy
New Zealand Institute for Crop & Food Research, Ltd., NZL
Jeffrey A. Lockwood
University of Wyoming, US
Abstract
Scientific theories have often been used to justify social actions. In the 19th century, Darwinian concepts were used to vindicate both greed and racism, and statistical patterns served as a means of rationalizing human brutality and resource distributions. In more recent times, complexity theories have been used as moral justification of social inequities. We focus particularly on the discovery that many physical, biological, and social measures tend toward a power or lognormal function. In a social context, such a function describes a situation with a very small number of very wealthy people, a small number of people with medium wealth, and an overwhelming majority of people with virtually nothing. With the causative mechanisms of such distributions having been proposed, this subdiscipline of complexity has taken on the qualities of a scientific law, from which a range of practical applications have been derived―including social prescriptions. Arguing that unequal distribution of wealth follows a natural law, these prescriptions propose that we have no choice but to accept it. The purpose of our paper is three-fold: 1. to briefly describe the nature and prevalence of power and lognormal distributions as a case-study in complexity theory; 2. to explore the overt and subtle use of the naturalistic fallacy as a means by which scientists and policy makers derive moral principles from empirical foundations, and; 3. to examine the role of free-will in the context of natural law as a means of escaping a nihilistic determinism. We show that lognormal-like distributions are indeed widespread. However, we also show that: 1. there are many exceptions of systems that tend to a more egalitarian distribution, demonstrating that ‘escape’ from the inequality of extreme lognormal patterns is possible, and; 2. society therefore has a choice of dedicating energy to establish and maintain an egalitarian distribution of resources; there is no moral or scientific justification for accepting without argument a strongly unequal distribution.
Introduction: The POLO distribution
Pareto, (1897) was perhaps the first to recognize that a complex, social parameter―individual wealth―followed the regular pattern that we now know as a power or lognormal function 1. Given the former is simply a particular case of the latter, Halloy, (1998) provided some clarity by referring to power or lognormal distributions under the unified term of ‘POLO’ (see Figure 1). POLO distributions have been subsequently found to describe a wide range of social, political and economic values (Galton, 1879; Limpert, et al., 2001; Hamada, 2004), including such unexpected measures as the sizes of cities (Zipf, 1949; Eeckhout, 2004). These patterns were also found to be widespread in biological, physical, and astronomical systems (Preston, 1948; May, 1975, 1981; Sugihara, 1980), leading to a plethora of synonyms and related terms (e.g., scale-free systems, edge of chaos, criticality) and debates about their meaning (Brown, et al., 2000; Li, et al., 2004; Halloy & Whigham, 2004; Arita, 2005).
In recent years, the POLO distribution has been elevated from a purely descriptive observation of a mathematical regularity into the realm of a natural law, although diverse causative mechanisms are still being debated (Zipf, 1949; MacArthur, 1960; Bak, 1997; Halloy, 1998; Arita. 2005; Wright, 2005). In brief, the POLO abundance distribution appears to act as a ‘pattern attractor’, an archetype to which complex systems tend in the absence of countervailing forces or constraints. The attractive force which aggregates resources in the POLO distribution has been formalized through a gravity equation. Resources are attracted to agents in proportion to their existing ‘mass’ (expressed in terms of resources already possessed) and in inverse proportion to the ‘distance’ (expressed in terms of difficulty, which may be a function of spatial separation but need not be) to the resource to be obtained (Barabási & Albert, 1999; Halloy & Whigham, 2004; Soares, et al., 2005). To illustrate the nature of POLO distributions and the underlying causative mechanisms, we consider the distributions of land, people, and wealth2.
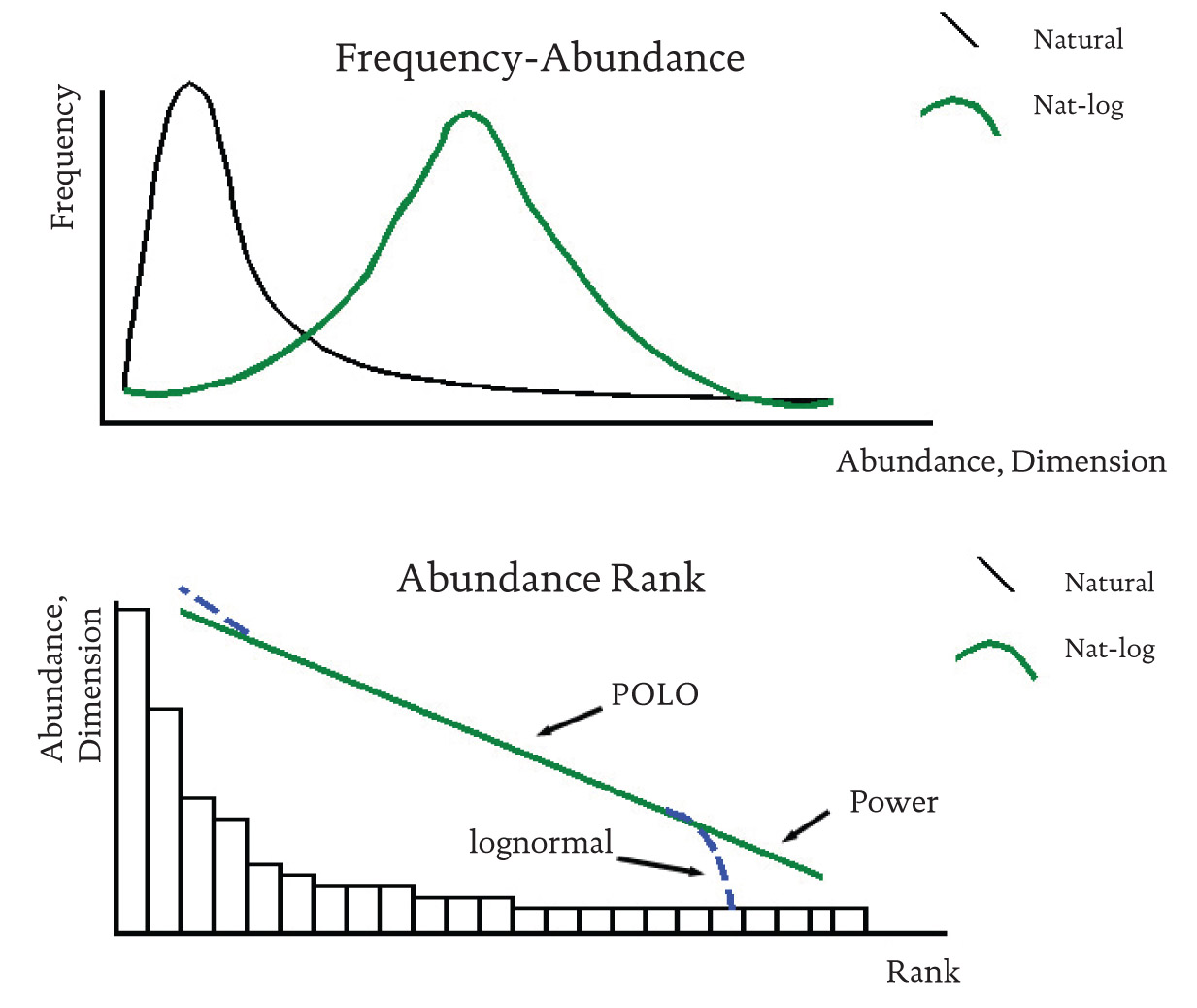
Figure 1 The POLO (power, lognormal) pattern as manifest infrequency-abundance and abundance-rank distributions
Exemplars of the POLO distribution: Land and population distributions
The attraction principle of complex systems suggests that the distribution of resources among competing peoples of the world should approximate a POLO pattern, if unconstrained. The amount of land controlled by nation states (agents) is a reasonable expression of resources. Countries have been historically gaining and losing large portions of land in a highly dynamic (mostly violent) game of competition. As predicted by theory, the areas of nations approximates a POLO distribution (see Figure 2a), maintaining a similar pattern over time (1960-1990) despite very large changes in the individual countries possessing land. Notably, the distance from the POLO decreased substantially from 1960 to 1990 (see Table 1), a fact which may be related to a release from the political constraints of colonization and the emergence of international competition and exchange. Both in 1960 and 1990 the distribution is biased toward an excess of large countries. Thus, unless outside force is applied (e.g., a strong United Nations or a shift of power from countries to multinational corporations), the next decades will likely see the continued breakup of large countries.
Unlike land, world population is a more fluid resource, particularly with the present population explosion, and our analysis revealed that population distribution approximates the POLO pattern better than land area. This is expected from measuring a ‘resource ’ which is exchanged much more freely among nations. It also conforms to the prediction that small departures from the POLO (due to historical accidents or acts of human free will) tend to decrease with time unless other forces are at work3.
Economic resource distributions among companies
The pattern shown by nations may become increasingly irrelevant to world affairs as the mechanism for power and resource distribution shifts to multinational corporations. Based on thousands of manufacturing companies, Stanley, et al. (1995) found that sales, as well as other economic parameters, almost perfectly fit a lognormal. The size of these organizations should also reflect a POLO distribution, as long as their development is not significantly constrained by social rules or ethical considerations. We found that the pattern of resources (wealth represented by market value) shown by the 1,000 largest corporations approximates a truncated lognormal distribution (see Figure 3).
Figure 2 Size distribution of (a) nations in the world and (b) states and territories in the USA. Chi^2/n values for these are given in Table 1.
| Parameter | 1960 | 1990 | |
| World, all nations | n units | 146 | 191 |
| Land Area | 4.06* | 0.88* | |
| Population | 0.49* | 0.30* | |
| USA, all territories | n units | 68 | 57 |
| Land Area | 1.55* | 1.19* | |
| Population | 0.77* | 1.21* | |
| USA, 50 states | n units | 50 | 50 |
| Land Area | 0.96* | 0.96* | |
| Population | 0.27 | 0.13 |
Table 1 Distance from the lognormal in the abundance distribution of land area and population controlled by nation-states. NB Distance expressed as chi/n* for the distribution including 0s at both ends. Asterisks indicate significant difference from lognormal at P<0.05*.
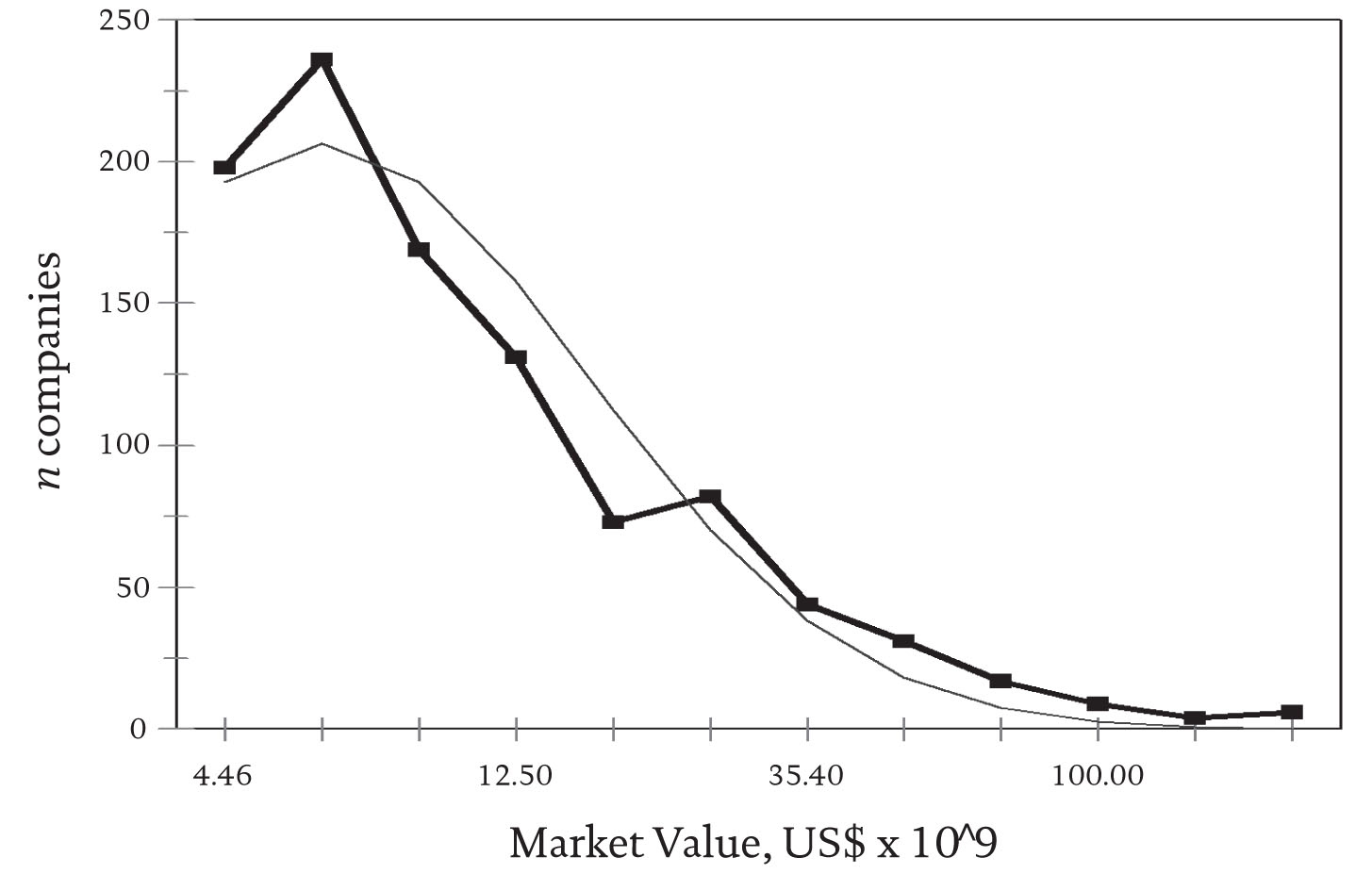
Figure 3 Distribution of wealth (■) and lognormal fit (-) among 1000 largest multinational companies (from The Global 1000, Business Week, 7 July 1997).
Applications of resource distributions
Given the ubiquity of the POLO distribution, scientists have proposed a range of practical applications. The most benign uses involve ecological indicators (Patrick, 1963; Gray, 1981; Nelson, 1987; Hill & Hamer, 1998; Kevan, 1999). More worrisome applications have also emerged. Zipf, (1949) showed that departure from a POLO distribution of human populations among cities preceded the US Civil War and World Wars I and II. He stopped short of contending that such a deviation could predict, or even justify, a tendency to war or conflict, but the implications were apparent. More recently, however, the POLO distribution has been used to derive and defend social prescriptions of unequal wealth (Preston, 1950) and private vs. public transport systems (Bak, 1997), and these uses are cause for ethical concern. Indeed, justifiable concern would seem to extend beyond these explicit statements. Although few scientists go as far, many are willing to make forceful statements of universality of POLO patterns (and laws thereof) and implicitly suggest that there is no escape from such patterns.
The naturalistic fallacy: ‘Is’ implies ‘ought’ An historical perspective
Menand, (2001) provides an excellent overview of the way in which science was used to formulate and justify moral positions in the 19th century. In 1800, probability theory and statistics converged in what was known as the Law of Errors, made famous by Pierre-Simon Laplace. Astronomers had sought a means of finding the true location of celestial objects, given the variation among scientific observations. The method of least squares provided the answer they sought, and Laplace saw no reason to limit this approach to physical data. He proposed that the Law of Errors could be applied to any phenomenon that varied, including human behavior.
The real breakthrough in applying the normal distribution to social data was made by Adolph Quetelet, (1846), who began his seminal work with the assertion that, “Man is born, grows up and dies according to certain laws which have never been studied.” Quetelet discovered remarkable regularities in the French murder rate (categorized by the method of killing), and he contended that the mean was the true value, with higher or lower rates being “errors.” The Law of Errors, he maintained, provided the means for deriving social laws that were every bit as determinate as the law of gravity. Indeed, he called his new science, “social physics.”
The appeal of statistics was that it revealed an order beneath what had appeared to be randomness. Even if individuals were unpredictable, their aggregate behavior conformed to natural law. Later in the 19th century, this desire for order―a hope that appears to motivate modern scientists, even those developing chaos theory today―played a substantial role in the acceptance of evolution. Darwin proposed natural selection as an orderly process that sorted out the chance events of biological change. The idea that the world was self-regulating conferred upon statistical and morphological patterns a ‘cosmic seal of approval’ that provided the moral foundation for the political doctrines of individualism and laissez fair capitalism. Free markets, like unfettered natural systems, would not devolve into anarchy, as some worried, but through the pursuit of individual self-interest aggregate efficiency would emerge. And this optimal pattern would not just be understandable in terms of science, it would be morally virtuous.
This leap from science to ethics was perhaps most powerfully expressed by Thomas Henry Huxley, an abolitionist who argued that slavery was unnecessary. White people did not need a social institution to do that which natural law made inevitable. He maintained that the “laws of social gravitation” would prevent blacks from ascending to stations beyond their natural limits. Although some people objected to this racist characterization, the greater concern was with regard to the philosophical implications of natural law. Such scientific expressions were seen as denying free will, reducing human behavior to deterministic formulae.
The conceptual move from science (a descriptive enterprise which endeavors to divulge the nature of physical existence) to ethics (a normative undertaking which aspires to reveal the nature of virtue and duty) was the fundamental transition that has been most recently termed the naturalistic fallacy. However, the more fundamental problem―that one cannot validly derive a conclusion about ‘what ought to be’ from a premise concerning ‘what is’―was first identified in the 18th century by David Hume. For example, from the assertion that a ring is made of gold it does not follow that the ring is valuable. We must also know that gold is valuable, and arguing for the validity of this ‘missing’ premise is precisely the problem.
From ‘is’ to ‘ought’ in complexity
Within the field of complexity, the leap from ‘is’ to ‘ought’ can be traced back to Preston, (1950). He suggested that although most people (the poor) would want to see more equality, extreme taxation to achieve this would lead to a static, zero-income society. Preston argued that,
“Perhaps, indeed, we ought not to try to change it [the lognormal distribution of wealth]. It is not always wise to try to change the laws of nature. Success does not usually attend such attempts, and if success is only to be expected when all life has ceased and nothing moves any longer in the economic system, we should hardly welcome the success. We might do far better to try to understand the law, and the causes that bring it about, than to try to change it out of indignation and without understanding.”
More recently, Bak, et al. (1988) explained that the process of ‘self-organized criticality’ was the mechanism accounting for power distributions. Bak (1997) then moved from description to prescription:
“Maybe Greenspan and Marx are wrong. The most robust state for an economy could be the decentralized self-organized critical state of capitalistic economics, with fluctuations of all sizes and durations. The fluctuations of prices and economic activity may be a nuisance (in particular if it hits you), but that is the best we can do! The self-organized critical state with all its fluctuations is not the best possible state, but it is the best state that is dynamically achievable.”
Bak’s statements epitomize, in a nutshell, the forceful beliefs which have led the International Monetary Fund (IMF) and World Bank to coerce many countries into economic programs which have maintained or increased inequality, human suffering and poverty (UN-DESA, 2005). This conceptual leap shows how complexity theory can be used to endorse a normative position. Such a move is particularly worrisome in this case, given that self-organized criticality is known to lead to chaotic termination of large parts of the system (e.g., mass extinctions) as well as to dynamic stability. Scientists working with POLO distributions are not the only ones to be using complexity as a means of deriving normativity.
Holling, et al. (2000) and Holling, (2001) have explicitly taken the leap from ‘is’ to ‘ought’ in research concerning economic, ecological, and social systems. Using the model of an adaptive cycle, Holling, (2001) not only describes the complex feedback loop of human systems, but consistently refers to this process in value-laden terms (e.g., “positive change,” “creativity,” “invigorated,” and “safe”) and describes alternative pathways as being “degraded” and “maladaptive.” Holling, et al.’s (2000) report to the MacArthur Foundation refers to dynamics other than the adaptive cycle as being pathological, and they argue that “bad regional policy and management can typically be corrected.” The form of this correction is a matter of enticing or coercing these failed societies to conform to Holling’s law of growth. Most notably, one of the three criteria that Holling, (2001) advances for a theoretical framework is that it “be dynamic and prescriptive, not static and descriptive” (emphasis added).
Thus, workers in the field of complex economic and social systems are deriving ethical norms from mathematical models. Economic development and wealth distribution are not simply understood in terms of the adaptive cycle and POLO distributions, but the fundamental processes have a modern-day ‘cosmic seal of approval’ conferred by conformation to natural law. But does it truly follow that we should consider them to be ‘the best achievable’ outcomes, as Holling and Bak imply?
Natural laws and ethical principles
Whether the move from description to prescription is defensible depends on the resolution of positivist versus transcendentalist ethics. One of the leading scientific advocates of positivism is E. O. Wilson, who refers to this approach as empirical ethics. In 1975, he argued in his landmark book Sociobiology (Wilson, 1975) that “ethics should be biologized.” Wilson contended that ethics is nothing more than a biological phenomenon arising from complex epigenetic rules. He developed this line of thinking even further in Consilience (Wilson, 1998), wherein he maintains that the natural sciences will provide the foundation for all human interpretations of the world, including art, spirituality, and morality. Ethics is merely “conduct favored consistently enough throughout a society to be expressed as a code of principles.” As such, ethics can be dismissed as a social crutch of diminishing relevance, a modern-day ‘god of the gaps’4.
However, even if the empiricists are correct―and there is plenty of reason to contend otherwise―this line of argument may not lead to positivistic ethics. That is, one might contend that the epigenetic rules of human nature actually compel a transcen-dental ethics. The human mind has arguably evolved beyond the limits of materialistic explanation and reductionist experience. As such, we are now free to think and act outside of the rules that constrain pre-conscious organisms.
There are other philosophical concerns with deriving the moral from the empirical. In Principia Ethica, Moore, (1903) built on Hume’s earlier analysis of the is-ought problem and both named and clearly explicated what we know as the naturalistic fallacy. Using the argument that one cannot logically leap from the factual ‘is’ to the normative ‘ought’, Moore showed that one cannot extract ethical principles from science. This position is grounded in Kant’s (1890) contention that to act morally is to act freely, and materialistic determinism precludes genuinely ethical behavior. Indeed, many and perhaps most modern philosophers advocate some form of transcendental ethics in which morality may be informed by, but is not reducible to, material facts.
Thus, the natural laws that lead to particular distribution patterns are not ‘good’ simply because they exist. This naturalistic fallacy is particularly tempting in the context of contemporary environmental concerns. Deep ecology (Sessions, 1995; Katz, et al., 2000) and other systems of environmental philosophy ascribe intrinsic value to nature. Hence, it is a small, but problematic, step to conclude that what is natural―a POLO distribution, for instance―must be good. In the 19th century, the study of natural history was linked to Christian values via the connection between the creation and the Creator (Barber, 1980). Using this religious endorsement of nature as being a manifestation of the divine, social Darwinists applied natural selection to justify how economic survival of the fittest reflected the will of God. Today, the linkage of nature to virtue is not explicitly religious (although spiritual arguments abound in this context; see Devall & Sessions, 1985) but the normative value of being ‘natural’ still serves as a foundation on which socio-economic prescriptions derived from Darwinism and complex systems are advocated.
However, even the staunch ethical transcendentalist must take seriously at least the central notion of the ethical empiricist: What ‘is’ (or more accurately, what ‘can be’) is relevant to what ‘ought’ to be. In short, Kant’s precept that ‘ought implies can’ suggests that if we are incapable of performing an act then we cannot be morally compelled to do so. Although the empiricist is unable to derive what we ought to do, s/he might be able to reveal what we cannot be obligated to do. If we are unable to escape from a POLO distribution of resources, then there is no ethical argument that such a pattern is wrong or that we should work towards some better arrangement.
The naturalistic constraint: ‘Ought’ implies ‘can’
Can we escape natural ‘law’?
Natural laws are more properly called ‘forces’ or ‘tendencies’ in a human context5. These laws describe the mechanisms that push or pull a system toward a particular condition or outcome, but forces can be counteracted by other forces, their effects neutralized or even reversed6. However, the notion of opposing forces is overlooked in the search for a universal, or at least unified, under-standing of complexity. Bak (1997) contends that, “Self-organized criticality is a law of nature for which there is no dispensation,” and this sentiment pervades Holling’s (2001) work on adaptive cycles.
Such assertions can result in ethical fatalism. In a relatively benign context, Bak (1997) justifies the irregularity of traffic by arguing that, “the critical state, with [traffic] jams of all sizes, is the most efficient system. The system has self-organized to the critical state with the highest throughput of cars.” However, it is not clear that we can equate efficiency (by any definition) with what is desirable, let alone what is good7. Many people may be happier with a lesser throughput if that meant they were not even occasionally caught in massive traffic jams. We can choose to engineer highways or use mass transit systems that allow predictable, even if less efficient, flows of traffic.
Consider a better known force and the absurd implications of acceding to physical law. The force of gravity dictates that our ‘natural’ posture is a prone position. However, most of the time we counteract this force by applying energy to sit, stand, or walk. Indeed, we blatantly defy gravity and steady state conditions by flying in machine s that are heavier than air. Yet, even when flying we haven’t ‘escaped’ gravity; we are simply applying forces that counter that of gravity. Not only do we counteract the law of gravity, but we have no ethical compunctions in doing so and might well contend a life spent lying flat would be an immoral waste of human potential. Indeed, there are many examples of natural systems which push themselves away from a POLO distribution through the development of appropriate rules. Such qualitative changes towards and away from the POLO have happened many times in evolution when organisms have evolved from indefinite growth (i.e., no bounds to growth and competition) to limited growth and vice-versa. After having published papers showing the prevalence of the lognormal, Preston, (1980) made a special effort to highlight that there are also exceptions.
But keeping away from the lognormal is not without cost. There is a ‘price’ to pay for defying gravity or maintaining a resource distribution other than the POLO. However, in many cases we are free to decide if the benefits justify the costs8. We can choose to deviate from a POLO distribution of wealth through expending ‘social energy’ in the form of laws, taxes, morals, gossip, religion, or other such resources (Sen, 1973, 1987; Boehm, 1993). Furthermore, social resources such as education, transportation, and medicine have been variously disconnected from a POLO distribution of wealth. During the 20th century it became possible, in at least some countries, to learn, move about, and remain healthy independent―or nearly so―of personal finances. However, recent changes in the societal values of many industrial nations has led to a diminishment of ‘social energy’ and a reversion to more POLO distributions (US Census Bureau, 1997; O’Connor, 1995; UN-DESA, 2005)9.
Should we escape the natural law of POLO?
The law of complex system structure (resource attraction) tells us that in the absence of countermanding forces, purely selfish agents acting in explicit competition for resources will lead to an increasingly unequal (more POLO) distribution of wealth (Halloy, 1998; Barabási & Albert, 1999; Halloy & Whigham, 2004). Of course, we do not mean to suggest that capitalism is a passive economic system; even the most capitalistic economies constrain greed to some extent. But given that we can deviate from a POLO distribution of resources, should we?
In that we are considering the ethical distribution of resources, the language and insights of justice would seem most appropriate to consider. There are various approaches to understanding justice, but Rawls’s (1971) theory is particularly compelling and comprehensible. In essence, he contends that to decide what is fair, one should act in a manner consistent with not knowing one’s own status in life. Behind this ‘veil of ignorance’ a person will select that course of action that is most just, because his/her own place in the consequent world is equally likely to be that of any one of the affected individuals. It seems that most people, if placed behind the veil, would not choose a POLO distribution of wealth, food or medicine given the overwhelming odds of finding themselves among the desperately poor, hungry, and sick of the world.
We would hasten to note that the ‘natural’ or POLO distribution is not inherently or necessarily immoral for all resources. Many non-vital resources reflecting human wants, rather than human needs, can be justly allocated in this manner. For example, given the range of aesthetic sensibilities, it may be entirely fair for a few people to own most of the rap music CDs, while many people own few, and most people own none.
So why do many people seem to accept, even prefer, a POLO distribution even for vital resources? We can only touch on this important and difficult question, which deserves a treatise in itself. However, in the words of Mary Wollstonecraft, a 19th century feminist philosopher, “Most of the evils of life arise from a desire of present enjoyment that outruns itself.” Many people who may well have sought long and worked hard to secure their place in the right tail of the POLO distribution[10], rationalize their position―and the weakening of social investment that would foster a more egalitarian distribution―based on the beliefs that: 1) unlimited material gain is a source of happiness, 2) one’s own wealth is unrelated to another’s poverty, and 3) higher productivity provides a trickle-down of benefits to all sectors of society10.
Perhaps the most compelling explanation of our apparent preference for POLO distributions of resources is rooted in the work of the existentialist philosophers such as Arthur Schopenhauer, S0ren Kierkegaard, Friedrich Nietzsche, Edmund Husserl, Martin Heidegger, Albert Camus and Jean-Paul Sartre (Kaufman, 1988; Cooper, 1999; Marino, 2004). The central and relevant concept that they offered in the context of understanding the human affinity for allowing ourselves to become the subjects of external laws, forces and dictates lies in the contention that western culture has fallen into a slave morality. Many people have abrogated personal responsibility to the authority of the Church or science. But these institutions and their ‘truths’ are human constructs, not objective, eternal, mind-independent realities. Existentialists contend that while we may be constrained by our condition (these philosophers differ in terms of the extent to which they believe we are limited in this regard), we are entirely free to choose how we respond to the world. They call upon humans to become masters of their own condition―to act from internal integrity and authenticity rather than from obedience to the external tyrants of religion or reason.
Acquiescing to the rule of law (whether it be purportedly that of logic, God, government, or society) is dehumanizing, but it is also profoundly comforting. As a slave of moral or scientific masters, we needn’t struggle with perennial questions, take responsibility for creating value, commit to autonomous action, or construct an ethical life. Accepting that we make the world―neither creating reality by whim nor discovering preexisting ‘truths’―is a frightening prospect. Rather than being cast adrift, most of us cling desperately to false gods, illusionary certainties, religious potentates, and scientific sovereigns. And POLO promises to become a modern, authoritative buoy. Although many people may well have struggled to secure a place in the right tail of the POLO distribution, the existentialists would contend that they have not wrestled with the essential question of what it means to be a ‘winner’ of a game of pawns whose moves are dictated by vacuous rules imposed by arbitrary authorities. The superficial and illusory victory of material wealth comes at staggering moral and spiritual cost.
Conclusions
As communication technologies, transportation systems, and ecological interdependencies continue to unite people around the world, it may be reasonable to propose that the greatest moral challenge facing society in the 21st century will be the just distribution of resources on a planetary scale. Along with this expansion of the human network has come the emergence of radically new ways of understanding complex systems such as global human society. These promising approaches to perceiving how human and ecological systems ‘are’ can be classified in the broad category of the complexity sciences. But as exciting as these lines of investigation might be, they are not immune from the errors of earlier forms of scientific inquiry. Using the naturalistic fallacy, social Darwinists provided a rationale for favoring the wealthy more than a century ago. And several authors in contemporary complexity science have made a similar, dangerous error in reasoning.
Although complexity encompasses far more than Preston’s patterns, Bak’s self-organized criticality, or Holling’s adaptive cycles, these programs represent worrying efforts to jump from complexity theory to normative claims. We know of no counter-examples (i.e., subdisciplines whose investigators have explicitly avoided―or warned against
using their scientific findings as a basis for ethical claims). As such, we maintain that there are sufficient grounds for concern that some contemporary scientists, in the area of complexity, are providing a fundamentally flawed justifications for the unequal distribution of resources by misrepresenting natural laws.
No scientist would doubt that natural laws and forces are a reality, but nor should any of us make the mistake of reducing the world to these terms. The reality of human freedom and social will are as evident and compelling in complex systems as any material form or mathematical dictate. By avoiding the wicked irony in which complexity is simplified to the terms of physical determinism, we come to understand that although the attraction toward the POLO is a natural law, the resultant pattern is not inevitable. Human societies have the choice of letting the attraction lead to unequal distributions, or investing in efforts to achieve a fair allocation of resources.
Notes
References
Arita, M. (2005). “Scale-freeness and biological networks,” Journal of Biochemistry, ISSN ,138: 1-4.
Bak P. (1997). How nature works. The science of self-organized criticality, Oxford, UK: Oxford University Press, ISBN 0387947914.
Bak, P. and Chen, K. (1991). “Self-organized criticality,” Scientific American, ISSN 0036-8733, 264: 26-33.
Bak, P., Tang, C. and Wiesenfeld, K. (1988). “Self-organized criticality,” Physical Review A, ISSN 1094-1622, 38: 364-374.
Barabási, A. L. and Albert, R. (1999). “Emergence of scaling in random networks,” Science, ISSN 1095-9203, 286: 509-512.
Barber, L. (1980). The heyday of natural history, 1820-1870, New York, NY: Doubleday, ISBN 022401448X.
B eder, S. (2003). Power play: The hidden costs of deregulating and privatizing power, Auckland, NZ: Scribe, ISBN 0908011970.
Boehm, C. (1993). “Egalitarian society and reverse dominance hierarchy,” Current Anthropology, ISSN 0011-3204,34: 227-254.
Brown, J. H., Marquet, P. A. and Taper, M. L. (1993). “Evolution of body size: Consequences of an energetic definition of fitness,” American Naturalist, ISSN 0003-0147,142:573-584.
Brown, J. H., West, G. B. and Enquist, B. J. (2000). “Scaling in biology: Patterns and processes, causes and consequences,” in J. H. Brown and G. B. West (eds.), Scaling in biology, Oxford, UK: Oxford University Press, ISBN 0195131428, pp. 1-24.
Collins, S. (1987). Rogernomics: Is there a better way? Wellington, NZ: Pitman, ISBN 0908575750.
Cooper, D. E. (1999). Existentialism: A reconstruction, Oxford, UK: Blackwell, ISBN 0631213236.
Dalziel, P. (1999). “Benefits failed to materialize,” Otago Daily Times, 20th July, p.13.
Devall, B. and Sessions, G. (1985). Deep ecology, Salt Lake City: Peregrine Smith, ISBN 0879052473.
Eeckhout, J. (2004). “Gibrat’s law for (all) cities,” American Economic Review, ISSN 0002-8282, 94: 1429-1451.
Fechner, G. T. (1860). Elemente der psychophysik, Leipzig, Germany: Breitkopf und Härtel.
Fechner, G. T. (1897). Kollektivmasslehre, Leipzig, Germany: Engelmann.
Galton, F. (1879). “The geometric mean, in vital and social statistics,” Proceedings of the Royal Society, 29: 365-367.
Gell-Mann, M. (1994). The quark and the jaguar: Adventures in the simple and the complex, New York, NY: W. H. Freeman, ISBN 0716727250.
Gray, J. S. (1981). “Detecting pollution induced changes in communities using the log-normal distribution of individuals among species,” Marine Pollution Bulletin, ISSN 0025-326X, 12:173-176.
Groth, B. H. A. (1914). “The golden mean in the inheritance of size,” Science, ISSN 1095-9203, 39: 581-584.
Halloy, S. R. P. (1998). “A theoretical framework for abundance distributions in complex systems,” Complexity International, ISSN 1320-0682, 6:12.
Halloy, S. R. P. (1999). “The dynamic contribution of new crops to the agricultural economy: Is it predictable?” in J. Janick (ed.), Perspectives on new crops and new uses, Alexandria, VA: ASHS Press, ISBN 0961502703, pp. 53-59.
Halloy, S. R. P. and Barratt, B. (1999). “Patterns of species abundance as indicators of ecosystem status,” in A. Holt, K. Dickinson and G. W. Kearsley (eds.), Environmental indicators, Dunedin, NZ: Environmental Policy and Management Research Centre, University of Otago, p. 87.
Halloy, S. R. P. and Whigham, P. A. (2004). “The lognormal as universal descriptor of unconstrained complex systems: a unifying theory for complexity,” in R. Stonier, H. Qing-Long and L. Wei (eds.), Proceedings of the 7th Asia-Pacific complex systems conference, Cairns, QLD, Australia, pp. 309-320.
Hamada, H. (2004). “A generative model of income distribution 2: Inequality of the iterated investment game,” Journal of Mathematical Sociology, ISSN 0022-250X, 28: 1-24.
Hammond, C. S. C. (1964). Hammond’s world atlas and gazetteer, Maplewood, NJ: Hammond.
Harte, J. (2004). “The abundance and distribution of Species at multiple spatial scales,” http://www.santafe.edu/events/abstract/211.
Hill, J. K. and Hamer, K. C. (1998). “Using species abundance models as indicators of habitat disturbance in tropical forests,” Journal of Applied Ecology, ISSN 0021-8901, 35: 458-460.
Holling, C. S. (2001). “Understanding the complexity of economic, ecological, and social systems,” Ecosystems, ISSN 1432-9840, 4: 390-405.
Holling, C. S, Folke, C., Gunderson, L. and Mäler K. G. (2000). “Resilience of ecosystems, economic systems and institutions,” final report to the John D. And Catherine T. MacArthur Foundation.
Hutchinson, G. E. (1953). “The concept of pattern in ecology,” Proceedings of the Academy of Natural Sciences of Philadelphia, ISSN 0097-3157, 105: 1-12.
Kant, I. (1890). Critique of pure reason, Amherst, NY: Prometheus, ISBN 0879755962 (1990).
Kapteyn, J. C. (1903). Skew frequency curves in biology and statistics, Groningen, The Netherlands: Noordhoff, Astronomical Laboratory.
Kapteyn, J. C. (1916). “Skew frequency curves in biology and statistics,” Receuil des Travaux Botaniques Néerlandais, Groningen, XIII: 105-158.
Katz, E., Light, A. and Rotherberg, D. (eds.). (2000). Beneath the surface: Critical essays in the philosophy of deep ecology, Cambridge, MA: MIT Press, ISBN 0613911342.
Kaufman, W. A. (ed.). (1988). Existentialism: From Dostoevsky to Sartre. New York, NY: Plume, ISBN 0452009308.
Kevan, P. G. (1999). “Pollinators as bioindicators of the state of the environment: Species, activity and diversity,” Agriculture, Ecosystems and Environment, ISSN 01678809, 74: 373-393.
Li, L., Alderson, D., Tanaka, R., Doyle, J. C. and Willinger, W. (2004). “Towards a theory of scale-free graphs: Definition, properties, and implications (extended version),” http://arxiv.org/PS_cache/cond-mat/pdf/0501/0501169.pdf.
Limpert, E., Stahel, W. A. and Abbt, M. (2001). “Log-normal distributions across the sciences: Keys and clues,” BioScience, ISSN 0006-3568, 51: 341-352, http://stat.ethz.ch/~stahel/lognormal/bioscience.pdf.
MacArthur, R. H. (1960). “On the relative abundance of species,” American Naturalist, ISSN 0003-0147, 94: 25-36.
Marino, G. (ed.). (2004). Basic writings of existentialism, New York, NY: Modern Library, ISBN 0375759891.
May, R. M. (1975). “Patterns of species abundance and diversity,” in M. L. Cody and J. M. Diamond (eds.), Ecology and evolution of communities, Cambridge, MA: Harvard University Press, ISBN 0674224442, pp. 81-120.
May, R. M. (1981). “Patterns in multi-species communities,” in R. M. May (ed.), Theoretical ecology: Principles and applications, 2nd edition, London, UK: Blackwell Scientific Publications, ISBN 0721662056, pp. 197-227.
McAlister, D. (1879). “The law of the geometric mean,” Proceedings of the Royal Society, 29: 367-376.
Menand, L. (2001). The metaphysical club: A story of ideas in America, New York, NY: Farrar, Straus & Giroux, ISBN 0374528497.
Mitzenmacher, M. (2004). “A brief history of generative models for power law and lognormal distributions,” Internet Mathematics, ISSN 1542-7951, 1: 226B251.
Moore, G. E. (1903). Principia ethica, New York, NY: Prometheus, ISBN 0879754982 (1988).
Nelson, W. G. (1987). “An evaluation of deviation from the log-normal distribution among species as a pollution indicator in marine benthic communities,” Journal of Experimental Marine Biology and Ecology, ISSN 0022-0981,113:181-206.
Newman, M. E. J. (2005). “Power laws, Pareto distributions and Zipf’s law,” http://arxiv.org/pdf/cond- mat/0412004.
Nobuhara, H. and Numata, N. (1954). “Essentials of the law of geometrical progression: Studies on the fundamental structure of biological populations. III,” Bulletin of the Society of Plant Ecology (Japan), 3: 180-185.
O’Connor, J. (1995). Monitoring environmental progress, Washington, DC: World Bank, ISBN 0821333658.
Osborn, F. (1953). The limits of the Earth, Boston, MA: Little, Brown and Co., ASIN B0007DEZWE.
Pareto, V. (1897). Cours d’economie politique, republished as Manual of political economy, Augustus M. Kelley Publishers, ISBN 0678008817 (1969).
Patrick, R. (1963). “Structure of diatom communities under varying ecological conditions,” Annals of the New York Academy of Sciences, ISSN 0077-8923, 108: 353-358.
Perline, R. (2005). “Strong, weak and false inverse power laws,” Statistical Science, ISSN 0883-4237, 20: 68-88.
Preston, F. W. (1948). “The commonness, and rarity, of species,” Ecology, ISSN 0012-9658, 29: 254-283.
Preston, F. W. (1950). “Gas laws and wealth laws,” Scientific Monthly, ISSN 0096-3771, 71: 309-311.
Preston, F. W. (1980). “Noncanonical distributions of commonness and rarity,” Ecology, ISSN 0012-9658, 61: 88-97.
Prigogine, I. (1980). From being to becoming: Time and complexity in the physical sciences, San Francisco, CA: W.H.Freeman, ISBN 0716711087.
Quetelet, A. (1846). Théorie des probabilités, Paris.
Raunkiaer, C. (1918). “Recherches statistiques sur les formations végétales,” Biologiske Meddeleser Kongelige Danske Videnskabernes Selskab, 1: 1 -80.
Rawls, J. (1971). A theory of justice, Cambridge, MA: Belknap, ISBN 0674000781.
Sachs, J. (1999). “Helping the world’s poorest,” The Economist, ISSN 0013-0613, 352: 17-20.
Sen, A. K. (1973). On economic inequality, Oxford, UK: Clarendon Press, ISBN 0198281935.
Sen, A. K. (1987). On ethics and economics, New York, NY: Basil Blackwell, ISBN 0631164014.
Sessions, G. (ed.). (1995). Deep ecology for the 21st century, Boston, MA: Shambhala, ISBN 1570620490.
Shiode, N. and Batty, M. (2005). “Power law distributions in real and virtual worlds,” http://www.isoc.org/ inet2000/cdproceedings/2a/2a_2.htm.
Soares, D. J. B., Tsallis, C., Mariz, A. M. and da Silva, L. R. (2005). “Preferential attachment growth model and nonextensive statistical mechanics,” Europhysics Letters, 70: 70-76.
Stanley, M. H. R., Buldyrev, S. V., Havlin, S., Mantegna, R. N., Salinger, M. A. and Stanley, H. E. (1995). “Zipf plots and the size distribution of firms,” Applied Economics Letters, ISSN 1350-4851, 49: 453-457.
Stiglitz, J. E. (2002). Globalization and its discontents, New York, NY: W. W. Norton, ISBN 0393324397
Sugihara, G. (1980). “Minimal community structure: An explanation of species abundance patterns,” American Naturalist, ISSN 0003-0147, 116: 770-787.
The Ecologist. (1993). Whose common future?―Reclaiming the commons, London: Earthscan, ISBN 0865712778.
Thoreau, H. D. (1849). “Civil disobedience,” in J. W. Krutch (ed.), Walden and other writings by Henry David Thoreau, reprinted, New York: Bantam, ISBN 1586632116 (1982).
Thompson, D. A. W. (1942). On growth and form, 2 vols. Cambridge MA: Cambridge University Press, 0486671356 (1992).
Times Books. (1993). The Times atlas of the World―Comprehensive edition, London, UK: Times Books, Harper Collins, ISBN 0723004927.
UN-DESA. (2005). Report on the World social situation: The inequality predicament, United Nations Division for Social Policy and Development of the Department of Economic and Social Affairs, ISBN 9211302315.
US Census Bureau. (1997). http://www.census.gov/hhes/income/income97/in97dis.html.
Weber, H. (1834). De pulsa resorptione auditu et tactu. Annotationes anatomicae et physiologicae, Leipzig, Germany: Koehler.
Wilson, E. O. (1975). Sociobiology: The new synthesis, Cambridge, MA: Belknap, ISBN 0674002350 (2000).
Wilson, E. O. (1986). Biophilia, Cambridge, MA: Harvard University Press, ISBN 0674074424.
Wilson, E. O. (1998). Consilience: The unity of knowledge, New York, NY: Alfred A. Knopff, ISBN 0679450777.
Wright, I. (2005). “The social architecture of capitalism,” Physica A: Statistical Mechanics and its Applications, ISSN 0378-4371, 346: 589-620.
Zipf, G. K. (1949). Human behavior and the principle of least effort: An introduction to human ecology, reprinted (1972), New York, NY: Hafner Publishing Company, ASIN B0007FMHHW.