Systems theory and complexity
Part 2
Kurt A. Richardson ISCE Research, USA
Introduction
In the first part of the series (Richardson, 2004) I discussed four general systems laws / principles -namely, the 2nd law of thermodynamics, the complementary law, the system holism principle, and the eighty-twenty principle - in terms of complex-ity thinking. In this part I continue my analysis of systems theory, by considering the following laws / principles:
- Law of requisite variety;
- Hierarchy principle;
- Redundancy of resources principle;
- High-flux principle.
Law of requisite variety
The law of requisite variety was proposed by Ashby (1958a), and states that: “Control can be obtained only if the variety of the controller is at least as great as the variety of the situation to be controlled” (Skyttner, 2001). Ashby’s Law, as the law of requisite variety is sometimes known, is a simpler version of Shannon’s Tenth Theorem (Shannon & Weaver, 1949) which states that:
“...if a correction-channel has capacity H, then equivocation of amount H can be removed, but no more.” (Ashby, 1962: 273-274 - original emphasis).
Ashby also expressed this law in terms of the brain, which is recognized as a paradigm example of a complex system: “...the amount of regulatory or selective action that the brain can achieve is absolutely bounded by its capacity as a channel” (Ashby, 1962: 274, 1958b). A variation on Ashby’s Law, sometimes referred to as the Conant-Ashby Theorem, is that every good regulator of a system must contain a complete representation of that system.
Another way to view Ashby’s Law is that it is through control of the system of interest that the controller can prevent variety being transmitted from the system’s environment to the system itself. Therefore, control plays an imp ortant role in system maintenance (homeostasis) as well as system performance and activity. In this sense, system regulation / control acts as a buffer to external perturbations (or any perturbations that might push the system away from the behavior desired by the regulator / controller.
When applied to the control, or management, of organizations Ashby’s Law, in concert with the Darkness Principle (discussed in part 1 of this series), seems to deny the possibility of management if we limit our definition of management to be the control of a system in order to achieve particular predetermined outcomes. The Darkness Principle implies that the knowledge any manager might have of a particular organization is incomplete, suggesting that no manager has the requisite variety to control an organization, which is by definition, is more varied than him / herself. This would appear to be a show- stopper for management at least in terms oftotal control. Luckily in human system total control is not usually the control.
Two principles are key to the discussion that follows. The first might be called the principle of modularity, or the principle of horizontal emergence. This refers to the observation that complex systems tend to organize themselves into reasonably well-defined (interactive) modules. As such, the j ob of the manager is made easier as s/he need only concern him / herself with directing a sub-section, or module, of the entire organization. Of course, these modules are still more varied than the manager so control is not complete. Furthermore, the modules are not isolated and so inter-module exchanges may lead to unforeseen, and potentially unwanted, wider system effects. In addition, system variety can be imported through the so- called boundaries of any given module. Nonetheless, this phenomena does at least provide management with a bounded view of parts of the organization that facilitates robust (first order) interventions.
The other feature is the observation that complex systems self-organize themselves into hierarchies: the principle of vertical emergence. This principle allows management to consider particular levels of aggregation rather than the organization as a whole. Again, there is interaction between these different levels / scales, but as a first approximation they provide a means for management to focus on a particular part rather than the whole. Furthermore, it isn’t quite the case that lower level ‘parts’ integrate to form higher level ‘wholes’, i.e., the hierarchies that emerge in complex systems are not analogous to the simply nested hierarchies proffered by the reductionist view of physical matter. Nonetheless, simple hierarchical representations are often useful in the development of managerial interventions.
Given the potential for small causes to lead to large effects there is no reason why management should require complete knowledge of their organi-zation in order to achieve specific goals (assuming we don’t limit ourselves to meaning the exact achievement of specific goals all of the time). In reality, our under-standing is only required to tip the balance slightly in our favor, i.e., introduce a bias in which we succeed more often than we fail. Fully understanding the higher-order effects of small nudges in a complex orga-nization is not possible for any manager. Despite this lack of explicit understanding, experienced managers develop an effective implicit appreciation, or ‘feel’, for organizational management. Successful management is often regarded as artistry as much as it is science.
Although Ashby’s Law is not contradicted by complex system thinking, in the sense that it denies perfect control, there are a range of possible interven-tion types that can tip the balance in management’s favor. Management / control need not be absolute and first order in order for it to be effective. We must, however, accept that frequent failures and only partial successes are part of the complex organizational scen-ery and not a feature that will be removed with ever more sophisticated managerial theories.
Hierarchy principle
The principles of horizontal and vertical emergence can be explored in more detail using the example of Boolean networks. Of course, real world systems are rather more complex than the simplistic idealized world of Boolean networks. However, even though analysis of such networks will not provide the whole story, it will at least provide part of the story.
Skyttner, (2001) defines the hierarchy principle as:
“Complex natural phenomena are organized in hierarchies wherein each level is made up of several integrated systems. (p. 93).
It has been shown recently that Boolean networks (specifically certain types of cellular automata - CA) can exhibit hierarchical behavior. Figure 1 shows part of the space-time diagram for the simple CA (as in Part 1 I will not go into depth regarding the details of this particular analysis - the interested reader is encouraged to explore the references given). Even though the initial conditions selected for the particular instance of CA were selected randomly, a pattern emerges that is neither totally ordered nor totally chaotic (or quasi-random). Figure 1 is an example of a (behaviorally) complex CA as defined by Wuensche, (1999). We can regard Figure 1 as a micro-representation of the CA system being modeled.

Figure 1 An example of a ‘complex’ CA
If we examine Figure 1 carefully we might notice that certain areas of the space-time plot are tiled with a common sub-pattern - this can be referred to as a pattern basis. Hansen and Crutchfield (1997) demonstrated how an emergent dynamics can be uncovered by applying a filter to the space-time plot. Figure 2 shows the result of pattern-basis-filtering as applied to Figure 1. Once the filter is applied an underlying dynamics ‘emerges’ for all to see. What can we say about this alternative representation of the micro-detailed spacetime plot?
Firstly, we can develop an alternative macrophysics for this apparent dynamical behavior that appears entirely different from the micro-physics of the CA. If we see these two ‘physics’ side by side (Figure 3) it is plainly apparent how different they are. The micro-physics description uses a micro-language (Ronald, et al., 1999) (which is sometimes referred to as the ‘language of design’) comprised only of 0s and 1s, whereas the macro-language is comprised of an entirely different alphabet: α, β, γ+, γ-. There is no simple mapping between these two languages / physics, i.e., there is no way (currently) to move between the two languages without losing information - the translation is imperfect (as it is in the translation of human languages).

Figure 2 Pattern-basis-filtered CA
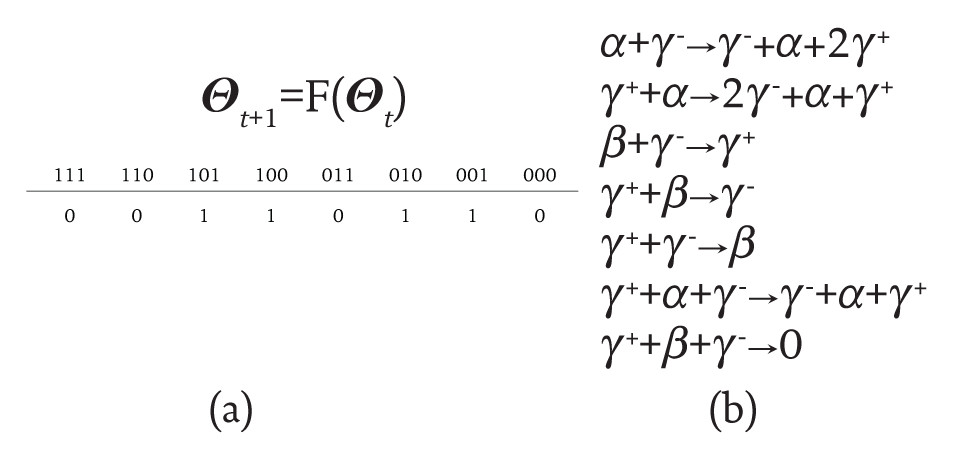
Figure 3 (a) The micro-physics of level-0 and (b) the macro-physics of level-1.
I have discussed the implications of incomplete translation in regard to the ontological status of emergent products and the relationship between micro and macro structures elsewhere (e.g. Richardson, 2004b) and so I won’t do so again here. I would like to add, however, that Hansen and Crutchfield (1997) designed further filters and used them to uncover higher-level structures. It was also found that although each level seemed to uncover new ‘parts’, the patterns at a particular level were not completely describable in terms of the level below. This suggests that the hierarchy is convoluted rather than nested.
Given that the ‘discovery’ of different levels seems to be dependent on the filter used, a case could be made that the results of many different filtering processes are of value (which might provide evidence for a radical relativism). Crutchfield, (1994) argues that the resulting patterns are not arbitrary, but instead play an important functional role in the system itself (leading to the concept of intrinsic emergence), i.e., not all patterns are necessarily significant. From a computational perspective it can be said that these hierarchical structures “support global information processing” (Crutchfield, 1994: 515).
So it seems that even in the simplest of complex systems hierarchical structures play an important role in their behavior.
Modularity
Bastolla and Parisi (1998) showed that modular structure plays an important role in the dynamics of simple complex systems. Their analysis showed that walls of constancy, through which no signal can pass, emerge which carve the system up into non-interacting modules. The overall dynamics of the system can then be understood in terms of the dynamics of the individual modules.
Figure 4 compares the modular structure of networks with qualitatively different topologies. As before, Boolean networks are utilized to demonstrate this particular phenomena.
Recently there has been somewhat of a renaissance in network theory with the discovery of structurally different network types. Whereas it used to be believed that most networks were random - i.e., composing of nodes that are connected randomly with each other - network researchers have now identified four broad categories of network topology: ordered, small world, scale-free as well as random (Barabasi, 2002). In this current experiment 10000 Boolean networks were created of each network type containing only fifteen nodes. Furthermore, despite the qualitative difference in connectivity, each network contained only 45 connections / edges. The functional rule for each node in each network realization was chosen randomly. Each network was reduced to its simplest form using the method presented in Richardson, (2005), and then the number of modules for a particular reduced form was determined by simply following the connections between nodes until closed sets were identified.
For the small networks studied it is apparent from Figure 4 that the predominant network type is those containing only one module. There are however some networks comprising two non-interacting modules (NB if many more networks were analyzed then it is likely that networks with even more modules would have been found). Figure 5 shows the modular distribution for random networks containing twenty nodes, indicating that for larger networks the largest number of modules possible increases (Bastolla & Parisi, 1998, confirmed that the probability of finding a single module decreases with system size). As an aside, it is interesting to note that for different topological types, the modular distribution is quite similar indeed in that the network ensembles are dominating by single module networks (it is notable though that all the small-world networks considered had only one module). Although the structure of these networks is quite different, it seems that some aspects of their dynamics are not quite do different.
Bastolla and Parisi (1998) suggest that “the spontaneous emergence of a modular organization in critical networks is one of the most interesting features of such systems.” (A reader of Adam Smith might argue that such emergence is a by-product of the least action principle). In real organizations, the emergence of completely non-interacting modules would seem unlikely - we would expect some interaction between modules, as well as evolution in modular size and number. However, even the simple Boolean network model illustrates the importance of modularity, which we might label as an example of horizontal emergence, in the behavior of complex systems. It would certainly be of interest to study small groups of people so as to observe how the numbers of modules evolve over a particular time period. We would expect that in some circumstances a small group would work together as one, and in others, the group would break-up into smaller units to embark on sub-activities. We would also expect that as the size of the group increases both logistical difficulties and the interference of other aspects of‘life’ would decrease the occurrence of large groups acting as a coherent whole.
Both the emergence of horizontal (modular) and vertical (hierarchical) structures in complex systems provide a means to understand and manipulate such systems, albeit in a limited way, without the necessity of complete system understanding (which is unobtainable).
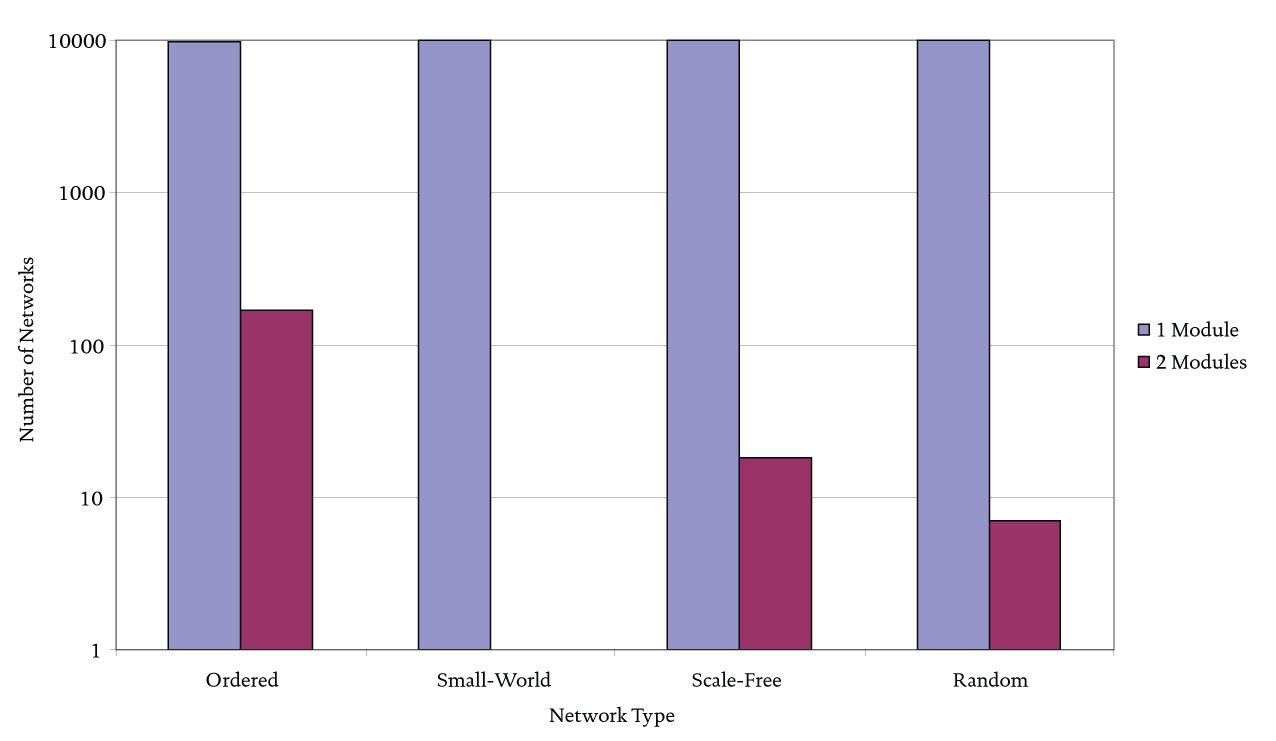
Figure 4 Profile of modular frequency in topologically different Boolean networks comprising fifteen nodes.
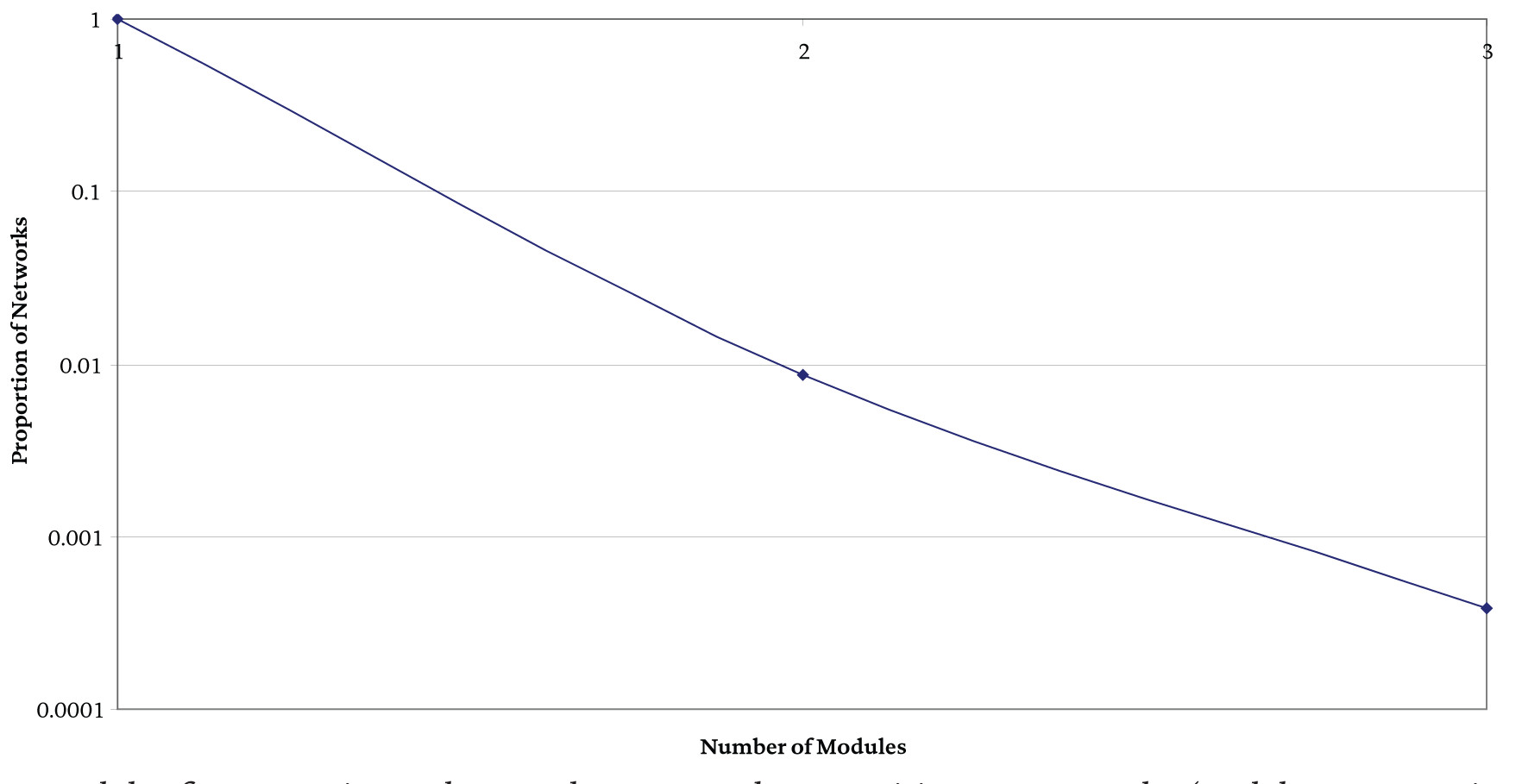
Figure 4 Modular frequency in random Boolean networks comprising twenty nodes. (NB Networks reducible to a single node are not included. If so, the proportion of single module reduced networks would be higher)
Again, complex systems research does not necessarily contradict the general systems principles examined herein. I do think, however, that the complex systems view of hierarchy is rather more sophisticated than the general systems view of hierarchy. The role of modular structure (sub-systems) is also not new to general systems theorists, although such structure is often regarded as hard-wired rather than an emergent property of the underlying dynamics.
Redundancy of resources principle
Skyttner, (2001) defines the redundancy of resources as the “[m]aintenance of stability under conditions of disturbance requires redundancy of critical resources” (p. 93). Other than the rather trivial example of shadowing certain sub-systems (modules) with copies of themselves, ready to take over at a moments notice, complex systems have a variety of means by which stability can be maintained under conditions of (external) disturbance.
The first relates to the 80/20 Principle that was discussed in the previous issue of E:CO. Research has shown that in complex systems not all nodes / parts participate in the (long-term) dynamics of the system as a whole. In Boolean networks these nodes are referred to as frozen nodes. These nodes play an important role in the emergence of modular structures. Furthermore, these (redundant) nodes act as a buffer to external perturbations. Rather than providing a replacement for certain nodes, these nodes absorb external perturbations and prevent them from perforating through the network. In terms of a system’s phase space, the presence of these redundant buffer nodes substantially increases the size of phase space, i.e., the total number of system states, which reduces the chance that external (random) perturbations might inadvertently target the more sensitive areas of phase space, therefore triggering a qualitative change in system dynamics, i.e., a bifurcation. It is this inclusion of elements, over and above those needed for the system to perform its designed function, that protect the system itself from even the smallest environmental fluctuations. When the physicist Schrödinger (1944/2000) pondered the question of why our brains are so large, in his What is Life?, his answer was that to maintain a coherent thought our brain needs to be sufficiently large such that it is not susceptible to atomic (quantum) randomness. Redundancy is essential in the creation and maintenance of containers in which ordered behavior can occur.
Within the emergent modular and hierarchical structures of complex systems - its sub-systems and levels - redundancy in feedback also provides a means for a system to maintain itself in the face of external forces. In a sufficiently well-connected module there are many routes from one node to any other node. If the signal between one node and another is blocked by the disruption of an intermediary node, then their may exist the opportunity for the signal to be transmitted via another route (although some kind of attenuation would be expected). This leads to the Redundancy of Information Theorem which states that errors in information transmission can be protected against (to any level of confidence required) by increasing the redundancy of the message s. This can mean both redundancy within the code itself through an appropriate coding scheme, or through transmission channel diversity.
High-flux principle
It amazes me that even a concept that seems so original to complexity thinking, such as far-from- equilibrium, has its systems theory equivalent. The London School of Economics’s Complexity Lexicon asserts that:
“When far-from-equilibrium, systems are forced to experiment and explore their space of possibilities and this exploration helps them discover and create new patterns of relationships.” (LSE, 2005)
These “new patterns of relationships” are often referred to as dissipative structures (Nicolis & Prigogine, 1989); that is, they consume energy. The source of this energy is an energy flux across the system / environment boundary, hence the term open systems, i.e., complex (dissipative) systems are not energetically isolated from their environment. The role these dissipative structures play in the system is not only in response to environmental perturbations. Energy can be expended on activities that do not seemingly contribute to the ongoing survival of the system itself, despite the fact that self-organizing dissipative systems are often portrayed only as systems that can respond and adapt to environmental changes.
The systems theory equivalent of far-from-equilibrium only concerns itself with the maintenance of the system in response to external perturbations. However, it very much includes the concept of far-from-equilibrium. The high-flux principle (Watt & Craig, 1988) suggests that:
“The higher the rate of the resource flux through the system, the more resources are available per time unit to help deal with the perturbation. Whether all resources are used efficiently may matter less than whether the rights ones reach the system in time for it to be responsive.” (Skyttner, 2001: 94).
There is an important difference though between complex systems theory and general systems
theory when it comes to understanding the role of energy in system development. The general systems view is that energy exchange across the system / environment boundary allows the system to maintain itself as is in the face of environmental changes / perturbations. The focus is therefore on qualitative stability. In complex systems theory the focus tends to be how the system / environment energy differential can be used by the system, not only to maintain itself in the face of external change, but also how it might (qualitatively) transform itself into quite a different system altogether - a question of evolution, not just maintenance.
Summary
In Part 2 of this series I have considered the efficacy of several more general systems principles / laws in terms of complex systems theory. In Part 3 several more principles / laws will be considered before I examine what general systems thinking has evolved into today. The evolution of systems thinking should be of interest to complexity thinkers, given that one could argue that complex systems thinking (CST) is in a similar state as general systems theory (GST) was 50 years ago. What I mean by this is that CST is very much dominated by quantitative analysis, whereas GST evolved to include fields such a critical systems thinking and boundary critique, which have a much more balanced view of quantitative and qualitative approaches to understanding systemic behavior.
References
Ashby, W. R. (1958a). An Introduction to Cybernetics, New York: Wiley.
Ashby, W. R. (1958b). “Requisite variety and its implications for the control of complex systems,” Cybernetica, 1: 8399.
Ashby, W. R. (1962). “Principles of the self-organizing system,” in H. Von Foerster and G. W. Zopf, Jr. (eds.), Principles of Self-Organization: Transactions of the University of Illinois Symposium, London: Pergamon Press. Reprinted in Emergence: Complexity and Organization, 6(1-2): 102-126.
Barabasi, A. - L. (2002). Linked: The New Science of Networks, Cambridge, MA: Perseus Publishing.
Bastolla, U. and Parisi, G. (1998). “The modular structure of Kauffman networks,” Physica D, 115: 219-233.
Crutchfield, J. P. (1994). “Is anything ever new? Considering emergence,” in G. A. Cowan, D. Pines and D. Meltzer (eds.), Complexity: Metaphors, Models, and Reality, Cambridge, MA: Perseus Books (1999).
Hansen, J. E. and Crutchfield, J. P. (1997). “Computational mechanics of cellular automata: An example,” Physica D, 103(1-4): 169-189.
LSE (2005). “Complexity Lexicon ," http://www.psych.lse.ac.uk/complexity/lexicon.htm. Downloaded 10th June.
Nicolis, G. and Prigogine, I. (1989). Exploring Complexity: An Introduction, New York: W. H. Freeman & Co.
Richardson, K. A. (2004a). “Systems theory and complexity: Part 1,” Emergence: Complexity and Organization, 6(3): 75-79.
Richardson, K. A. (2004b). “On the relativity of recognizing the products of emergence and the nature of physical hierarchy,” proceedings of the 2nd Biennial International Seminar on the Philosophical, Epistemological and Methodological Implications of Complexity Theory, January 7th-10th, Havana International Conference Center, Cuba.
Richardson, K. A. (2005). “Simplifying Boolean networks,” accepted for publication in Advances in Complex Systems.
Ronald, E. M. A., Sipper, A., and Capcarrére, M. S. (1999). “Testing for emergence in artificial life,” in Advances in Artificial Life: 5th European Conference, ECAL 99, volume 1674 of Lecture Notes in Computer Science, Floreano, D., Nicoud, J. -D., and Mondad, F. (eds.), Springer: Berlin, pp. 13-20.
Schrödinger, E. (1944/2000). What is Life? The Physical Aspect of the Living Cell, London: The Folio Society.
Shannon, C. E. and Weaver, W. (1949). The Mathematical Theory of Communication, Urbana: University of Illinois Press.
Skyttner, L. (2001). General Systems Theory: Ideas and Applications, NJ: World Scientific.
Watt, K. and Craig, P. (1988). “Surprise, Ecological Stability Theory,” in C. S. Holling (ed.), The Anatomy of Surprise, New York: John Wiley.
Wuensche, A. (1999). “Classifying cellular automata automatically: Finding gliders, filtering, and relating spacetime patterns, attractor basins, and the Z parameter,” Complexity, 4: 47-66.