Knowledge, Ignorance, and Learning

Prof Peter Allen
Cranfield University, ENG

Introduction

If we look at the dictionary definitions of science, we find “systematic and formulated knowledge.” Systematic is defined as “methodical, expressed formally, according to a plan.” If we look up complexity, we find “consisting of parts, composite, complicated, involved.” And the definition of complicated is “intricate, involved, hard to unravel.”

Putting these together, and excluding the “intricate and hard to unravel” part, a definition of systems science could be the systematic, formulated knowledge that we have about situations or objects that are composite. But already we can see the origins of the major branches of “complexity thinking,” whether one is discussing a complicated system of many parts, or alternatively what might be a relatively simple system of parts whose mutual interactions make them “hard to unravel.” We also see the fundamental paradox that is involved in the science of complexity, since it purports to be the systematic knowledge that we have about objects of study that will be either “intricate or hard to unravel.”

Systematic and formulated knowledge about a particular situation or object may be of different kinds. It could be what type of situation or object we are studying; what it is “made of;” how it “works;” its “history;” why it is as it is; how it may behave; how and in what way its behavior might be changed.

The science of complexity is therefore about the limits to the creation of systematic knowledge (of some of the above types) in situations or objects that are either “intricate or hard to unravel.”

This has two basic underlying reasons:

With today's enormously increased computational power, the first case is not necessarily a problem, whereas the second corresponds to what we shall call the science of complexity. We shall create a framework of systematic knowledge concerning the limits to systematic knowledge. This will take us from a situation that is so fluid and nebulous that no systematic knowledge is possible to a mechanical system that runs along a predicted path to a predicted equilibrium solution. Clearly, most of the problems that we encounter in our lives lie somewhere between these two extremes. What the science of complexity can do for us is allow us to know what we may reasonably expect to know about a situation. It can therefore banish false beliefs in either total freedom of action or total lack of freedom.

The identification of “knowledge” with “prediction” arose from the success and dominance of the mechanical paradigm in classical physics. This is understandable, but erroneous. While it is impressive to be able to predict eclipses, it is indeed “knowledge” to know, in a particular situation (playing roulette?), that prediction is impossible. In the natural sciences, for many situations it was possible to know what was going to happen, to predict the behavior, on the basis of the (fixed) behavior of the constituent components. The Newtonian paradigm based on planetary motion, the science of mechanics, applied to situations where this was true, and indeed in which the history of a situation, and knowledge as to “why it was as it is,” were not required for the prediction.

But of course, “mechanical systems” turn out to be a very special case in the universe! They may even exist only as abstractions of reality in our minds. The real world is made up of coevolving, interacting parts where patterns of interaction and communication can change over time, and structures can emerge and reconfigure.

KNOWLEDGE GENERATION

In the next two sections we set out a systematic framework of knowledge about the limits to knowledge. The different aspects of knowledge may be:

In previous papers Allen has presented a framework of “assumptions” that, if justified, lead to different limits to the knowledge one can have about a situation (Allen, 1985, 1988, 1993, 1994, 1998).

ASSUMPTIONS USED TO REDUCE COMPLEXITY TO SIMPLICITY

What are these assumptions?

  1. We can define a boundary between the part of the world that we want to “understand” and the rest. In other words, we assume first that there is a “system” and an “environment.”
  2. We have rules for the classification of objects that lead to a relevant taxonomy for the system components, which will enable us to understand what is going on. This is often decided entirely intuitively. In fact, we should always begin by performing some qualitative research to try to establish the main features that are important, and then keep returning to the question following the comparison of our understanding of a system with what is seen to happen in reality.
  3. The third assumption concerns the level of description below that of the chosen components or variables. It assumes that these components are “homogeneous:”

This assumption, if it can be justified, will automatically lead to a description over time that cannot change the average properties of the components. The “inside” of a component is not affected by its experiences. It leads to a description based on components with fixed, stereotypical insides. This is a simplification of reality that fixes the nature and responses of the underlying elements inside the components. It creates “knowledge” in the short term at the expense of the long. When we make this simplifying assumption, although we create a simpler representation, we lose the capacity for our model to “represent” evolution and learning within the system.

  1. The fourth assumption is that the individual behavior of the subcomponents can be described by their average interaction parameters. So, for example, the behavior of different employees in a business would be characterized by the average behavior of their job type. This assumption (which will never be entirely true) eliminates the effects of “luck” and of randomness and noise that are really in the system.

The mathematical representation that results from making all four of these assumptions is that of a mechanical system that appears to “predict” the future of the system perfectly.

A fifth assumption that is often made in building models to deal with “reality” is that of stability or equilibrium. It is assumed in classical and neoclassical economics, for example, that markets move rapidly to equilibrium, so that fixed relationships can be assumed between the different variables of the system. The equations characterizing such systems are therefore “simultaneous,” where the value of each variable is expressed as a function of the values of the others. Traditionally, then, “simple” models have been used to try to understand the world around us, as shown in Figure 1 overleaf. Although these can be useful at times, today we are attempting to model “complex” systems, leaving their inherent complexity intact to some extent. This means that we may attempt to build and study models that do not make all of these simplifying assumptions.

What is important about the statement of assumptions is that we can now make explicit the kind of “knowledge” that is generated, provided that the “necessary” assumptions can be made legitimately. Relating assumptions to outcomes in terms of types of model, we have the science of complexity.

THE SCIENCE OF COMPLEXITY

Having made explicit the assumptions that can allow a reduction in the complexity of a problem, we can now explore the different kinds of knowledge that these assumptions allow us to generate.

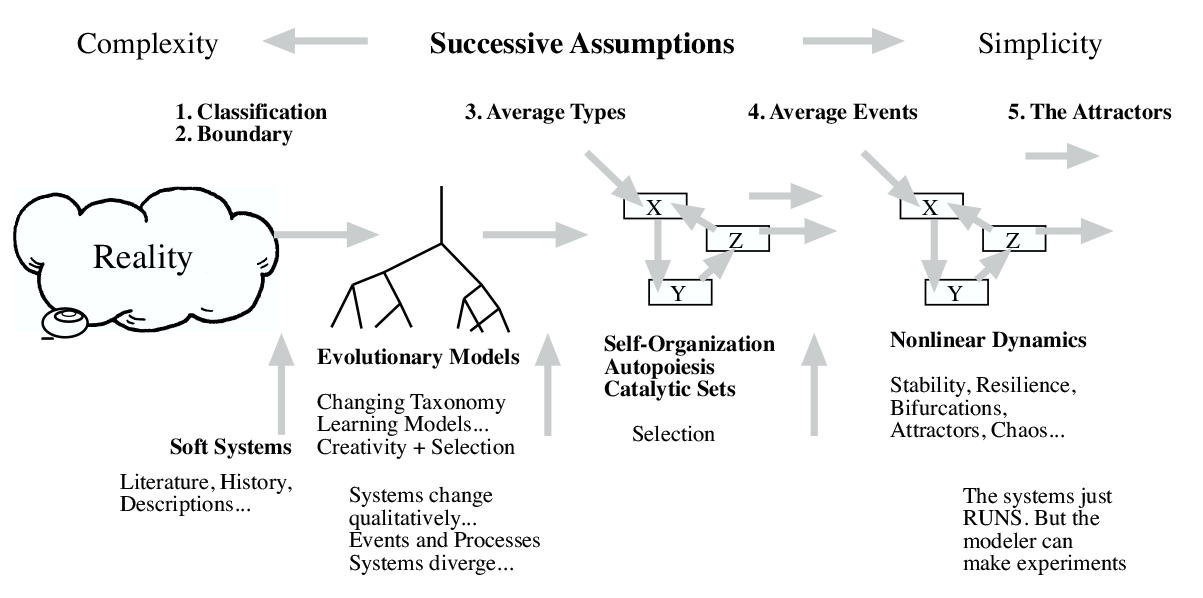
Figure 1. The assumptions made (left to right) in trading off realism and complexity against simplification and hence ease of understanding

EQUILIBRIUM KNOWLEDGE

If we can justifiably make all five assumptions above, and consider only the long-term outcome, then we have an extremely simple, hard prediction. That is, we know the values the variables will have, and from this can “calculate” the costs and benefits that will be experienced. Such models are expressed as a set of fixed relationships between the variables, calculable from a set of simultaneous equations.

Of course, these relationships are characterized by particular parameters appearing in them, and these are often calibrated by using regression techniques on existing data. Obviously, the use of any such set of equations for an exploration of future changes under particular exogenous scenarios would suppose that these relationships between the variables remained unchanged. In neoclassical economics, much of spatial geography, and many models of transportation and land use, the models that are used operationally today are still based on equilibrium assumptions. Market structures, locations of jobs and residences, land values, traffic flows, etc. are all assumed to reach their equilibrium configurations “sufficiently rapidly” following some innovation, policy, or planning action, so that there is an equilibrium “before” and one “after” the event or action, vastly simplifying the analysis.

The advantage of the assumption of “equilibrium” lies in the simplicity that results from having only to consider simultaneous and not dynamical equations. It also seems to offer the possibility of looking at a decision or policy in terms of stationary states “before” and “after” the decision. All cost/benefit analysis is based on this fundamentally flawed idea.

The disadvantage of such an approach, where an equilibrium state is simply assumed, is that it fails to follow what may happen along the way. It does not take into account the possibility of feedback processes where growth encourages growth, decline leads to further decline, and so on (nonlinear effects), which can occur on the way to equilibrium. In reality, it seems much more likely that people discover the consequences of their actions only after making them, and even then have little idea of what would have happened if they had done something else. Because of this, inertia, heuristics, imitation, and post-rationalization play an enormous role in the behavior of people in the real world. As a result, there is a complex and changing relationship between latent and revealed preferences, as individuals experience the system and question their own assumptions and goals. By simply assuming “equilibrium,” and calibrating the parameters of the relationships on observation, one has in reality a purely descriptive approach to problems, following, in a kind of post hoc calibration process, the changes that have occurred. This is not going to be very useful in providing good advice on strategic matters, although economists appear to have more influence on governments than do any other group of academics.

NONLINEAR DYNAMICS

Making all four assumptions leads to system dynamics, a mechanical representation of changes. Nonlinear dynamics (system dynamics) are what results generally from a modeling exercise when assumptions 1 to 4 above are made, but equilibrium is not assumed. Of course, some systems are linear or constant, but these are both exceptions, and also very boring. In the much more usual case of nonlinear dynamics, the trajectory traced by such equations corresponds not to the actual course of events in the real system but, because of assumption 4, to the most probable trajectory of an ensemble of such systems. In other words, instead of the realistic picture with a somewhat fluctuating path for the system, the model produces a beautifully smooth trajectory.

This illusion of determinism, of perfectly predictable behavior, is created by assuming that the individual events underlying the mechanisms in the model can be represented by their average rates. The smoothness is only as true as this assumption is true. Systems dynamics models must not be used if this is not the case. Instead, some probabilistic model based on Markov processes might be needed, for example.

If we consider the long-term behavior of nonlinear dynamical systems, we find different possibilities. They may:

An attractor “basin” is the space of initial conditions that lead to particular final states (which could be simple points, or cycles, or the surface of a strange attractor), and so a given system may have several different possible final states, depending only on its initial condition. Such systems cannot by themselves cross a separatrix to a new basin of attraction, and therefore can only continue along trajectories that are within the attractor of their initial condition. Compared to reality, such systems lack the “vitality” to jump spontaneously to the regime of a different attractor basin. If the parameters of the system are changed, however, attractor basins may appear or disappear, in a phenomenon known as bifurcation. Systems that are not precisely at a stationary point attractor can follow a complicated trajectory into a new attractor, with the possibility of symmetry breaking and, as a consequence, the emergence of new attributes and qualities.

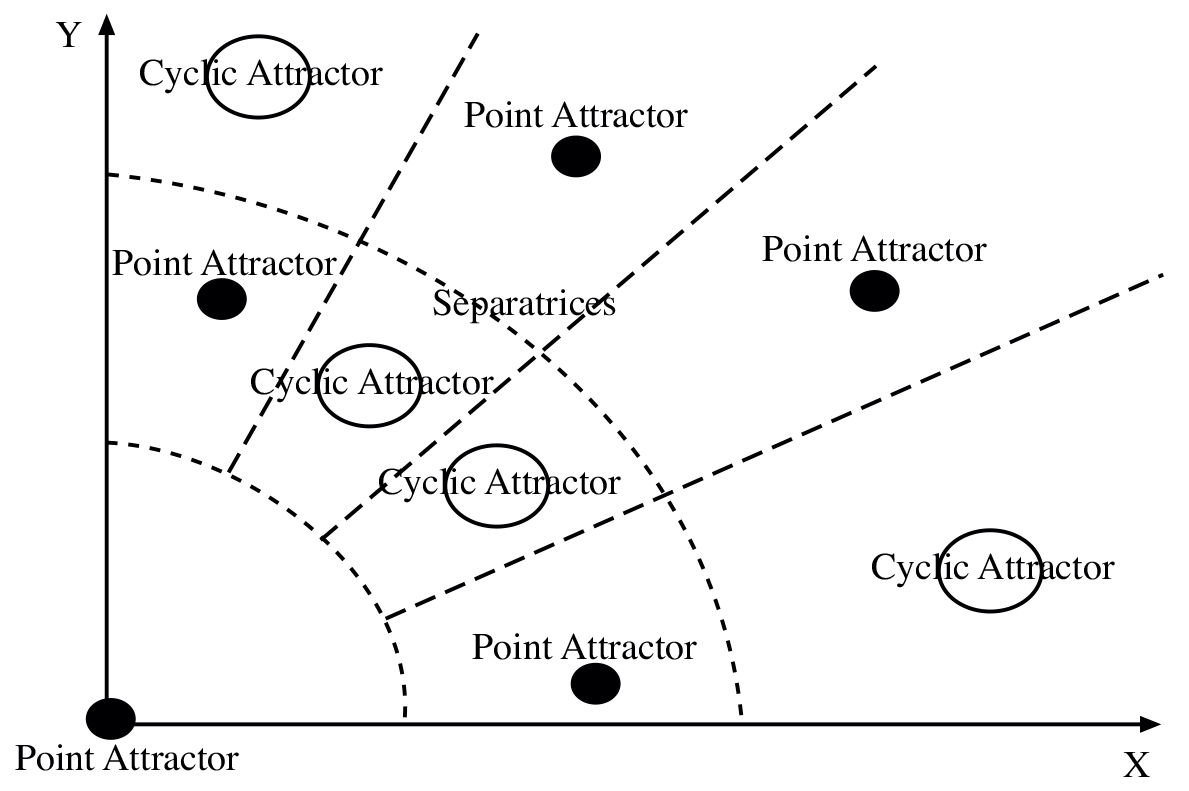
Figure 2. An example of the different attractors that might exist for a nonlinear system. These attractors are separated by “separatrices”

 

SELF-ORGANIZING DYNAMICS

Making assumptions 1 to 3 leads to self-organizing dynamic models, capable of reconfiguring their spatial organizational structure. Provided that we accept that different outcomes may now occur, we may explore the possible gains obtained if the fourth assumption is not made.

In this case, nonaverage fluctuations of the variables are retained in the description, and the ensemble captures all possible trajectories of our system, including the less probable. As we shall see, this richer, more general model allows for spontaneous clustering and reorganization of spatial configuration to occur as the system runs, and this has been termed “self-organizing.” In the original work, Nicolis and Prigogine (1977) called the phenomenon “order by fluctuation,” while Haken (1977) called it “synergetic,” and mathematically it corresponds to returning to the deeper, probabilistic dynamics of Markov processes (see, for example, Barucha-Reid, 1960) and leads to a dynamic equation that describes the evolution of the whole ensemble of systems. This equation is called the “master equation,” which, while retaining assumption 3, assumes that events of different probabilities can and do occur. So, sequences of events that correspond to successive runs of good or bad “luck” are included, with their relevant probabilities.

Each attractor is defined as being the domain in which the initial conditions all lead to the final result. But, when we do not make assumption 4, we see that this space of attractors has “fuzzy” separatrices, since chance fluctuations can sometimes carry a system over a separatrix across to another attractor, and to a qualitatively different regime. As has been shown elsewhere (Allen, 1988) for systems with nonlinear interactions between individuals, what this does is to destroy the idea of a trajectory, and gives to the system a collective adaptive capacity corresponding to the spontaneous spatial reorganization of its structure. This can be imitated to some degree by simply adding “noise” to the variables of the system. This probes the stability of any existing configuration and, when instability occurs, leads to the emergence of new structures. Such selforganization can be seen as a collective adaptive response to changing external conditions, and results from the addition of noise to the deterministic equations of system dynamics. Methods like “simulated annealing” are related to these ideas.

Once again, it should be emphasized that self-organization is a natural property of real nonlinear systems. It is only suppressed by making assumption 4 and replacing a fluctuating path with a smooth trajectory. The knowledge derived from self-organizing systems models is not simply of its future trajectory, but instead of the possible regimes of operation that it could potentially adopt. Such models can therefore indicate the probability of various transitions and the range of qualitatively different possible configurations and outcomes.

EVOLUTIONARY COMPLEX SYSTEMS

System components and subcomponents all coevolve in a nonmechanical mutual “learning” process. These arise from a modeling exercise in which neither assumption 3 nor assumption 4 is made. This allows us to clarify the distinction between “self-organization” and “evolution.” Here, it is assumption 3 that matters, namely, that all individuals of a given type, x say, are either identical and equal to the average type, or have a diversity that remains normally distributed around the average type. But in reality, the diversity of behaviors among individuals in any particular part of the system is the result of local dynamics occurring in the system. However, the definition of a “behavior” is closely related to the knowledge that an individual possesses. This in turn depends on the mechanisms by which knowledge, skills, techniques, and heuristics are passed on to new individuals over time.

Obviously, there is an underlying biological and cultural diversity due to genetics and to family histories, and because of these, and also because of the impossibility of transmitting information perfectly, there will necessarily be an “exploration” of behavior space. The mechanisms of our dynamical system contain terms that both increase and decrease the populations of different “behavioral” or “knowledge” types, and so this will act as a selection process, rewarding the more successful explorations with high payoff and amplifying them while suppressing the others. It is then possible to make the local micro diversity of individuals and their knowledge an endogenous function of the model, where new knowledge and behaviors are created and old ones destroyed. In this way, we can move toward a genuine, evolutionary framework capable of exploring more fully the “knowledge dynamics” of the system and the individuals that make it up.

Such a model must operate within some “possibility” or “character” space for behaviors that is larger than the one initially “occupied,” offering possibilities that our evolving complex system can explore. This space represents, for example, the range of different techniques and behaviors that could potentially arise. This potential will itself depend on the channeling and constraints that result from the cultural models and vocabulary of potential players. In any case, it is a multidimensional space of which we would only be able to anticipate a few of the principal dimensions.

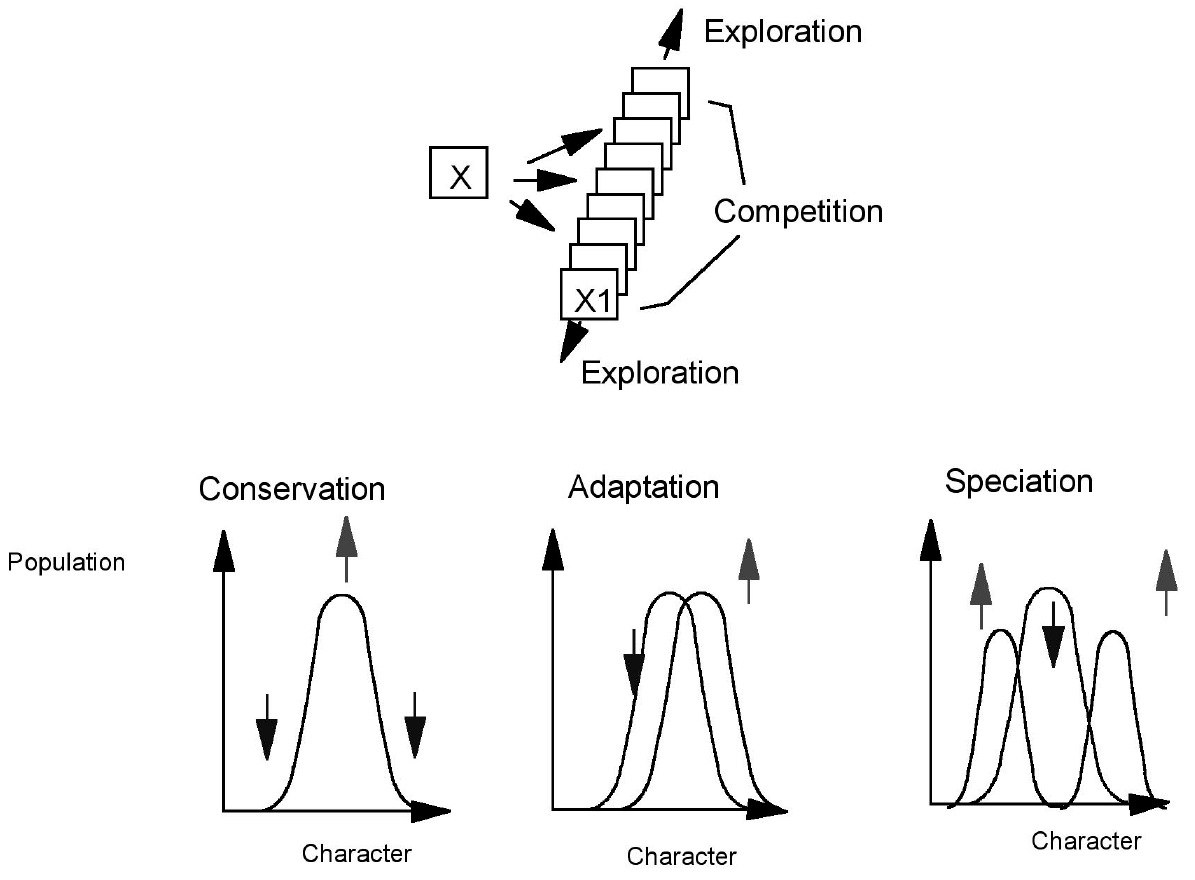
Figure 3 If eccentric types are always suppressed, then we have non-evolution. But, if not, then adaptation and speciation can occur

In biology, genetic mechanisms ensure that different possibilities are explored, and offspring, offspring of offspring, and so on spread out in character space over time, from any pure condition. In human systems, the imperfections and subjectivity of existence mean that techniques and behaviors are never passed on exactly, and therefore that exploration and innovation are always present as a result of the individuality and contextual nature of experience. Human curiosity and a desire to experiment also play a role. Some of these “experimental” behaviors do better than others. As a result, imitation and growth lead to the relative increase of the more successful behaviors, and to the decline of the others.

By considering dynamic equations in which there is an outward “diffusion” in character space from any behavior that is present, we can see how such a system would evolve. If there are types of behavior with higher and lower payoff, then the diffusion “uphill” is gradually amplified, while that “downhill” is suppressed, and the “average” for the whole population moves higher up the slope. This is the mechanism by which adaptation takes place. It demonstrates the vital part played by exploratory, nonaverage behavior, and shows that, in the long term, evolution selects for populations with the ability to learn, rather than for populations with optimal, but fixed, behavior.

In other words, adaptation and evolution result from the fact that knowledge, skills, and routines are never transmitted perfectly between individuals, and individuals already differ. However, there is always a shortterm cost to such “imperfection,” in terms of unsuccessful explorations, and if only short-term considerations were taken into account, such imperfections would be reduced. But without this exploratory process, there would be no adaptive capacity and no long-term future in a changing world.

If we return to our modeling framework in Figure 1, where we depict the tradeoff between realism and simplicity, we can say that a simple, apparently predictive system dynamics model is “bought” at the price of assumptions 1 to 4. What is missing from this is the representation of the underlying, inner dynamic that is really running under the system dynamics as the result of “freedom” and “exploratory error making.” However, if it can be shown that all “eccentricity” is suppressed in the system, evolution will itself be suppressed, and the “system dynamics” will then be a good representation of reality. This is the recipe for a mechanical system, and the ambition of many business managers and military people. However, if instead micro diversity is allowed and even encouraged, the system will contain an inherent capacity to adapt, change, and evolve in response to whatever selective forces are placed on it. Clearly, therefore, sustainability is much more related to micro diversity than to mechanical efficiency.

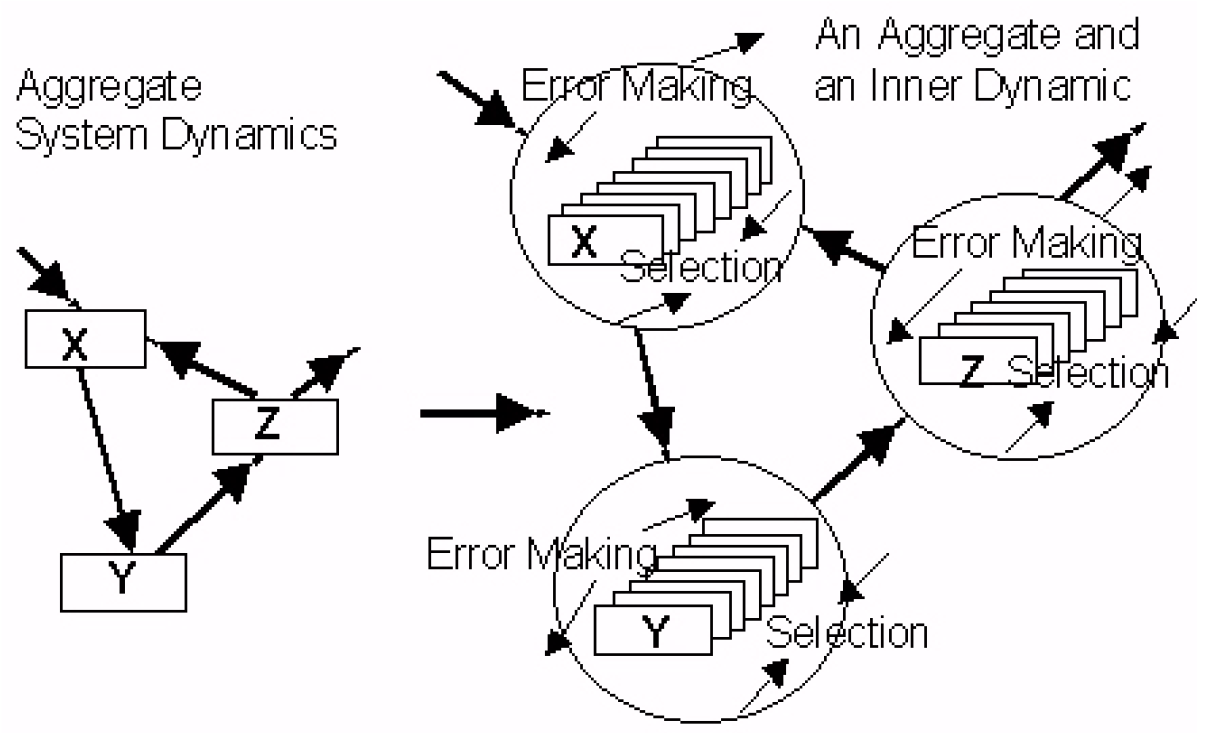
Figure 4 Without assumption 3 we have an “inner” dynamic within the macroscopic system dynamics. Micro diversity, in various possible dimensions, is differentially selected, leading to adaptation and emergence of new behaviors

Let us now examine the consequences of not making assumptions 3, 4, and 5. In the space of “possibilities,” closely similar behaviors are considered to be most in competition with each other, since they require similar resources and must find a similar niche in the system. However, we assume that in this particular dimension there is some “distance” in character space, some level of dissimilarity, at which two behaviors do not compete. In addition, however, other interactions are possible. For example, two particular populations i and j with characteristic behavior may have an effect on each other. This could be positive, in that side effects of the activity of j might in fact provide conditions or effects that help i. Of course, the effect might equally well be antagonistic, or neutral. Similarly, i may have a positive, negative, or neutral effect on j. If we therefore initially choose values randomly for all the possible interactions between all i and j, these effects will come into play if the populations concerned are in fact present. If they are not there, then obviously there can be no positive or negative effects experienced.

Figure 5 A population i may affect population j, and vice versa

A typical evolution is shown in Figure 6 overleaf. Although competition helps to “drive” the exploration process, what is observed is that a system with “error making” in its behavior evolves toward structures that express synergetic complementarities. In other words, although driven to explore by error making and competition, evolution evolves cooperative structures. The synergy can be expressed either through “self-symbiotic” terms, where the consequences of a behavior in addition to consuming resources is favorable to itself, or through interactions involving pairs, triplets, and so on. This corresponds to the emergence of “hypercycles” (Eigen & Schuster, 1979) and of “supply chains” in an economic system.

The lower right-hand picture in Figure 6 shows the evolution tree generated over time. We start off an experiment with a single behavioral

Figure 6 A two-dimensional possibility is gradually filled by the errormaking diffusion, coupled with mutual interaction. The final frame shows the evolutionary tree generated by the system

type in an otherwise “empty” resource space. The population initially forms a sharp spike, with eccentrics on the edge suppressed by their unsuccessful competition with the average type. However, any single behavior can only grow until it reaches the limits set by its input requirements, or, in the case of an economic activity, by the market limit for any particular product. After this, it is the “eccentrics,” the “errormakers,” that grow more successfully than the “average type,” as they are less in competition with the others and the population identity becomes unstable. The single sharply spiked distribution spreads, and splits into new behaviors that climb the evolutionary landscape that has been created, leading away from the ancestral type. The new behaviors move away from each other, and grow until in their turn they reach the limits of their new normality, whereupon they also split into new behaviors, gradually filling the resource spectrum.

While the “error-making” and inventive capacity of the system in our simulation is a constant fraction of the activity present at any time, the system evolves in discontinuous steps of instability, separated by periods of taxonomic stability. In other words, there are times when the system structure can suppress the incipient instabilities caused by innovative exploration of its inhabitants, and there are other times when it cannot suppress them and a new behavior emerges. It illustrates the fact that the “payoff” for any behavior is dependent on the other players in the system. Success of an individual type comes from the way it fits the system, not from its intrinsic nature. The important long-term effects introduced by considering the endogenous dynamics of micro diversity has been called evolutionary drive, and has been described elsewhere (Allen & McGlade, 1987a; Allen, 1990, 1998).

One of the important results of “evolutionary drive” was that it did not necessarily lead to a smooth progression of evolutionary adaptation. This was because of the “positive feedback trap.” This trap results from the fact that any emergent trait that feeds back positively on its own “production” will be reinforced, but that this feedback does not necessarily arise from improved performance in the functionality of the individuals. For example, the “peacock's tail” arises because the gene producing a male's flashy tail simultaneously produces an attraction for flashy tails in the female. This means that if the gene occurs, it will automatically produce preferentially birds with flashy tails, even though they may even function less well in other respects. Such genes are essentially “narcissistic,” favoring their own presence even at the expense of improved functionality, until such a time, perhaps, as they are swept away by some much more efficient newcomer. This can give a punctuated type of evolution, as “inner taste” temporally dominates evolutionary selection at the expense of increased performance with respect to the environment. This is like culture within an organization where success is accorded to those who are “one of us.” For example, the “model” or “conjecture” within an organization about the environment it is in and what is happening will tend to self-reinforce for as long as it is not clearly proved wrong. There is a tendency to institutionalize “knowledge” and “practice” so that actors are “qualified” to act providing they share the “normal” view. Such conformity and unquestioning acceptance of the company line are of seeming benefit in the short term, but are dangerous over the long term. In a static or very slowly changing world, problems may take a long time to surface, but in a fluid, unstable, and emergent situation, this would be disastrous in the longer term.

Much of conventional knowledge management therefore concerns the generation and manipulation of databases, and the IT issues raised by this. However, knowledge only exists as the interpretive framework that assigns “meaning” and “action” to given data inputs as the result of a particular system view. But the evolution of complex systems tells us that structural systemic change can and will occur, and therefore that any particular “interpretive framework” will need to be able to change. This means that any particular “culture” and set of practices should be continually challenged by dissidents, and rejustified by believers. Consensus may be a more frequent cause of death than is conflict.

Perhaps the real task of “management” is to create havens of “stability” for the necessary period within which people can operate with fixed rules, according to some set of useful “stories.” However, these would have to be transformed at sufficiently frequent periods if the organization is to continue to survive. Therefore, as a counterweight to the “fixed” part of the organization engaged in “lean” production, there would have to be the exploratory part charged with the task of creating the next “fixed” structure. This is one way in which knowledge generation and maintenance could be managed in some sectors.

THE LIMITS TO KNOWLEDGE

If we now take the different kinds of knowledge in which we may be interested concerning a situation, then we can number them according to:

  1. What type of situation or object we are studying (classification— “prediction” by similarity).
  2. What it is “made of” and how it “works.”
  3. Its “history” and why it is as it is.
  4. How it may behave (prediction).
  5. How and in what way its behavior might be changed (intervention and prediction).

Then we can establish Table 1, which therefore in some ways provides us with a very compressed view of the science of complexity.

Assumptions5432
Type of modelEquilibriumNonlinear dynamics (including chaos)Self-organizingEvolutionary
Type of systemYesYesYesCan change
CompositionYesYesYes butCan change
HistoryIrrelevantIrrelevantStructure changesImportant
PredictionYesYesProbabilisticLimited
Intervention and predictionYesYesProbabilisticLimited

Table 1 Systematic knowledge concerning the limits to systematic knowledge

Here, we should comment on the fact that we have considered models with at least assumptions 1 and 2. These concern situations where we believe we know how to draw a boundary between a system and its environment, and where we believe we know what the constituent variables and components are. But these could be considered as being a single assumption that chooses to suppose that we can understand a situation on the basis of a particular set of influences—a typical disciplinary academic approach with a ceteris paribus assumption. A boundary may be seen as limiting some geographic extension, while the classification of variables and mechanisms is really a region within the total possible space of phenomena.

A representation or model with no assumptions whatsoever is clearly simply subjective reality. It is the essence of the postmodern, in that it remains completely contextual. In this way, we could say that it does not therefore fall within the science of complexity, since it does not concern systematic knowledge. It is here that we should recognize that what is important to us is not whether something is absolutely true or false, but whether the apparent systematic knowledge being provided is useful. This may well come down to a question of spatio-temporal scales.

For example, if we compare an evolutionary situation to one that is so fluid and nebulous that there are no discernible forms, and no stability for even short times, we see that what makes an evolutionary model possible is the existence of stable forms, for some time at least. If we are only interested in events over very short times compared to those usually involved in structural change, it may be perfectly legitimate and useful to consider the structural forms fixed (i.e., we can make assumption 3). This doesn't mean that they are, it just means that we can proceed to do some calculations about what can happen over the short term, without having to struggle with how forms may evolve and change. Of course, we need to remain conscious that over a longer period forms and mechanisms will change and that our actions may well be accelerating this process, but nevertheless it can still mean that some self-organizing dynamic is useful.

Equally, if we can assume not only that forms are fixed but that in addition fluctuations around the average are small (i.e., can make assumptions 3 and 4), we may find that prediction using a set of dynamic equations provides useful knowledge. If fluctuations are weak, it means that large fluctuations capable of kicking the system into a new regime/attractor basin are very rare and infrequent. This gives us some knowledge about the probability that this will occur over a given period. So, our model can allow us to make predictions about the behavior of a system as well as the associated probabilities and risk of an unusual fluctuation occurring and changing the regime. An example of this might be the idea of a 10-year event and a 100-year event in weather forecasting, where we use the statistics of past history to suggest how frequent critical fluctuations are. Of course, this assumes the overall stationarity of the system, supposing that processes such as climate change are not happening. Clearly, when 100year events start to occur more often, we are tempted to suppose that the system is not stationary, and that climate change is occurring.

These are examples of the usefulness of different models and the knowledge with which they provide us, all of which are imperfect and not strictly true in an absolute sense, but some of which are useful.

Systematic knowledge, therefore, should not be seen in absolute terms, but as being possible for some time and in some situations, provided that we apply our “complexity reduction” assumptions honestly. Instead of simply saying that “all is flux, all is mystery,” we may admit that this is so only over the very long term (who wants to guess what the universe is for?). Nevertheless, for particular questions in which we are interested, we can obtain useful knowledge about their probable behavior by making these simplifying assumptions, and this can be updated by continually applying the “learning” process of trying to “model” the situation.

A FISHERIES EXAMPLE

The example of Canadian Atlantic Fisheries has been presented in several articles (Allen & McGlade, 1986, 1987b, 1988; Allen, 1997). It includes models of different types, equilibrium, nonlinear dynamics, and selforganizing. Here, we shall only describe a model that generates, explores, and manages the “knowledge dynamics” of fishermen in different ways. Our model (or story) is set in a spatial domain of 40 zones, with two fishing ports on the coast of Nova Scotia. The model/story recounts the fishing trips and catches of fishermen based on the knowledge they have of the location of fish stocks and the revenue they might expect by fishing a particular zone. This information comes essentially from the fishing activity of each boat and of the other boats, and therefore there is a tendency for a “positive feedback trap” to develop in which the pattern of fishing trips is structured by that of the catch—leading to self-reinforcement. Areas where fishing boats are absent send no information about potential catch and revenue. The parameters of the cod, haddock, and pollock are all accurate, as are the costs and data about the boats.

The spatial distribution of fishing boats has two essential terms. The first takes into account the increase or decrease of fishing effort in zone I, by fleet L, according to how profitable it is. If the catch rate is high for a species of high value, revenue greatly exceeds the costs incurred in fishing there, provided that the zone is not too distant from the port. Then effort will increase. If the opposite is true, effort will decrease. The second term takes into account the fact that due to information flows in the system (radio communication, conversations in port bars, spying, etc.), to a certain extent each fleet is aware of the catches being made by others. Of course, boats within the same fleet may communicate freely the best locations, and even between fleets there is always some “leakage” of information. This results in the spatial movement of boats, and is governed by the “knowledge” they have concerning the relative profits that they expect at the different locations.

This “knowledge” is represented in our model/story by the “relative attractivity” that a zone has for a particular fishing boat, depending on where it is, where its home port is, and what the skipper “knows.” For these terms we use the idea of “boundedly rational” decision makers who do not have “perfect” information or absolutely “rational” decisionmaking capacity. In other words, each individual skipper has a probability of being attracted to zone I, depending on its perceived attractivity. Since probability must vary between 0 and 1, we see that A must always be defined as positive. A convenient form, quite usual in economics, is:

Ai= eRUi

where Ui is a “utility function.” Ui constitutes the “expected profit” of the zone i, taking into account the revenue from the “expected catch” and the costs of crew, boat, and fuel, etc. that must be expended to get it.

In this way, we see that boats are attracted to zones where high catches and catch rates are occurring, but the information only passes if there is communication between the boats in i and in j. This will depend on the “information exchange” matrix, which will express whether there is cooperation, spying, or indifference between the different fleets. However, responses in general will be tempered by the distances involved and the cost of fuel.

In addition to these effects, however, our equation takes another very important factor into account, factor R. This expresses how “rationally,” how “homogeneously,” or with what probability a particular skipper will respond to the information he is receiving. For example, if I is small, then whatever the “real” attraction of a zone i, as expressed in U, the probability of going to any zone is roughly the same. In other words, “information” is largely disregarded and movement is “random.” We have called this type of skipper a stochast. Alternatively, if i is large, it means that even the smallest difference in the attraction of several zones will result in each skipper going, with probability 1, to the most attractive zone. In other words, such deciders put complete faith in the information they have, and do not “risk” moving outside of what they know. These

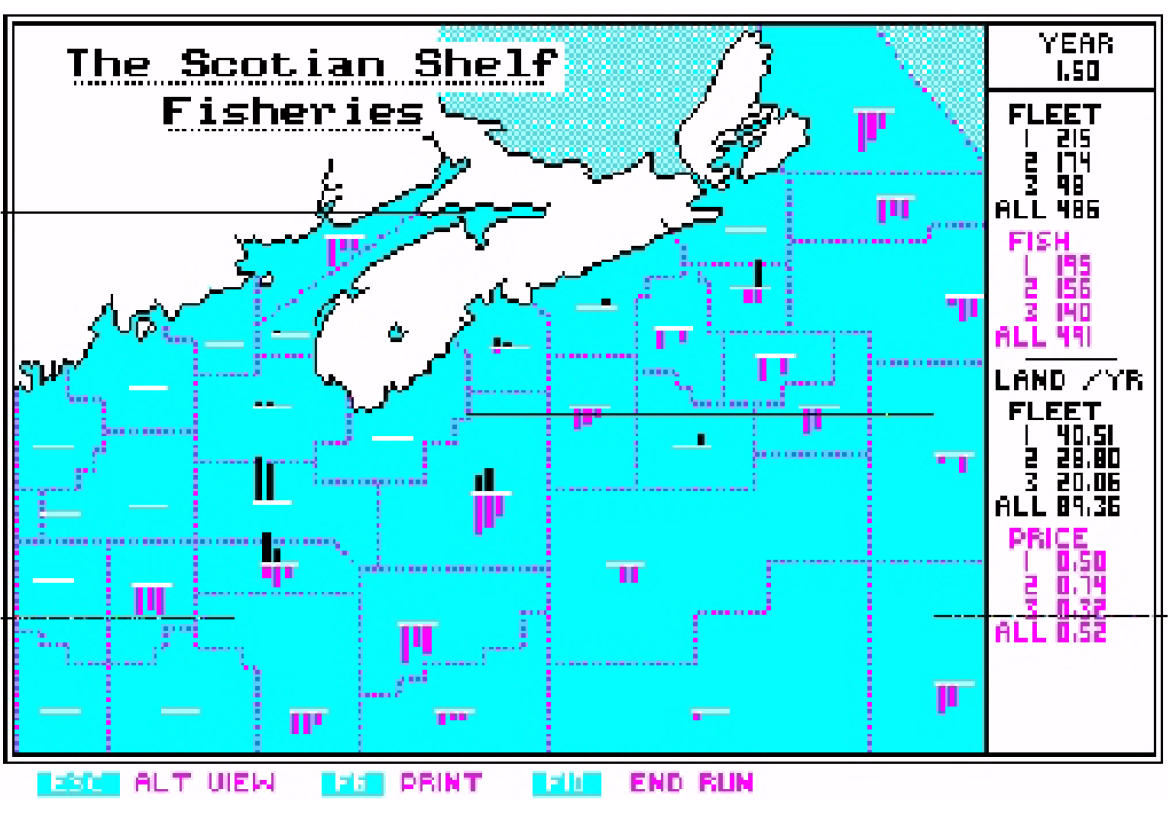
Figure 7 An initial condition of our fishing story. Two trawler fleets and one long liner fleet attempt to fish three species (cod, haddock, and pollock)

“ultra rationalists” we have called Cartesians. The movement of the boats around the system is generated by the difference at a given time between the number of boats that would like to be in each zone, compared to the number that actually are there. As the boats congregate in particular locations of high catch, so they fish out the fish population that originally attracted them. They must then move on the next zone that attracts them, and in this way there is a continuing dynamic evolution of fish populations and of the pattern of fishing effort. Let us describe briefly a key simulation that we have made of this model. We consider the competition between fleets 1 and 2 fishing out of port 1 in South West Nova Scotia. We start from the initial condition shown above and simply let the model run, with catches and landings changing the price of fish, and the knowledge of the different fleets changing as the distribution of fish stocks changes. We let the model run for 20 years, and see how the “rationality” I affects the outcome.

This is a remarkable result. The higher the value of R, the better the fleet optimizes its use of information (knowledge management?) and in the short term increases profits (e.g., R=3 or more). But, this does not necessarily succeed in the long term. Cartesians have a tendency to “lock in” to their first successful zone and stay fishing there for too long, because it is the only information available. These Cartesians are not “risk takers” who will go out to zones with no information, and hence they get

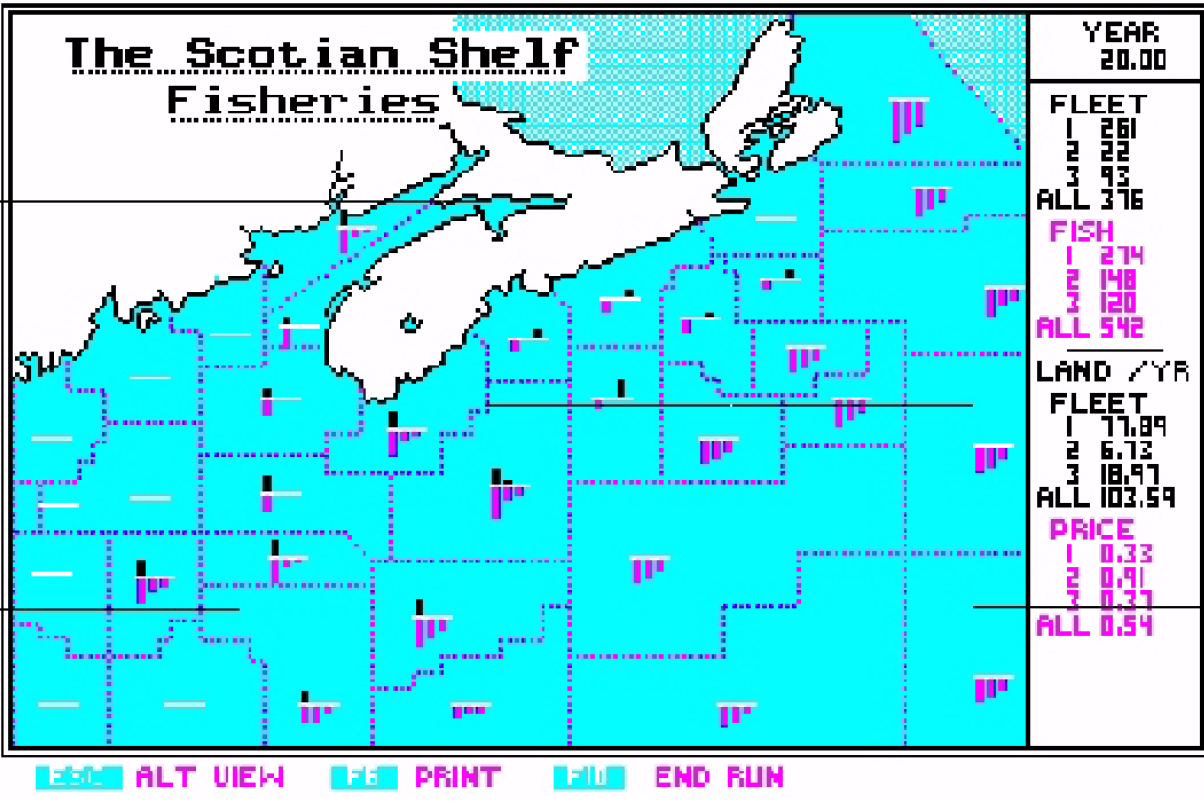
Figure 8 Over 20 years the stochast (R=.5) beats the Cartesian (R= 2), after initially doing less well

trapped in the existing pattern of fishing. The stochasts (R=.5), provided that they are not totally random (R less than .1), succeed in both discovering new zones with fish stocks, and also in exploiting those that they have already located. This paradoxical situation results from the fact that in order to fish effectively, two distinct phases must both be accomplished. First, the fish must be “discovered.” This requires risk takers who will go out into the “unknown” and explore—whatever present knowledge is. The second phase, however, requires that when a concentration of fish has been discovered, the fleet will move in massively to exploit this, the most profitable location. These two facets are both necessary, but call on different qualities.

Our fishing model/story can be used to explore the evolution of strategies over time. Summarizing the kinds of results observed, we find the following kind of evolutionary sequence:

The real point of these results is that they show us that there is no such thing as an optimal strategy. As soon as any particular strategy becomes dominant in the system, it will always be vulnerable to the invasion of some other strategy. Complexity and instability are the inevitable consequence of fishermen's efforts to survive, and of their capacity to explore different possible strategies. The important point is that a strategy does not necessarily need to lead to better global performance of the system in order to invade. Nearly all the innovations that can and will invade the fishing system lead to lower overall performance, and indeed to collapse. Thus, higher technology, more powerful boats, faster reactions, etc. all lead to a decrease in output of fish.

In reality, the strategies that invade the system are ones that pay off for a particular actor in the short term. Yet, globally and over a long period, the effect may be quite negative. For example, fast responses to profit/loss or improved technology will invade the system, but they make it more fragile and less stable than before. This illustrates the idea that the evolution of complexity is not necessarily “progress,” and the system is not necessarily moving toward some “greater good.”

EVOLUTIONARY FISHING: LEARNING HOW TO LEARN

We can now take our model/story to a further stage: We can build a model that will learn how to fish. To do this, we shall simply run fleets in competition with each other. They will differ in the parameters that govern their strategy: rationality, rate of response to profit and loss, which fleets they try to communicate with, etc. By running our model, some fleets will succeed and some fail. If we take out the failures when they occur, and relaunch them with new values of their strategy parameters, then we can see what evolves.

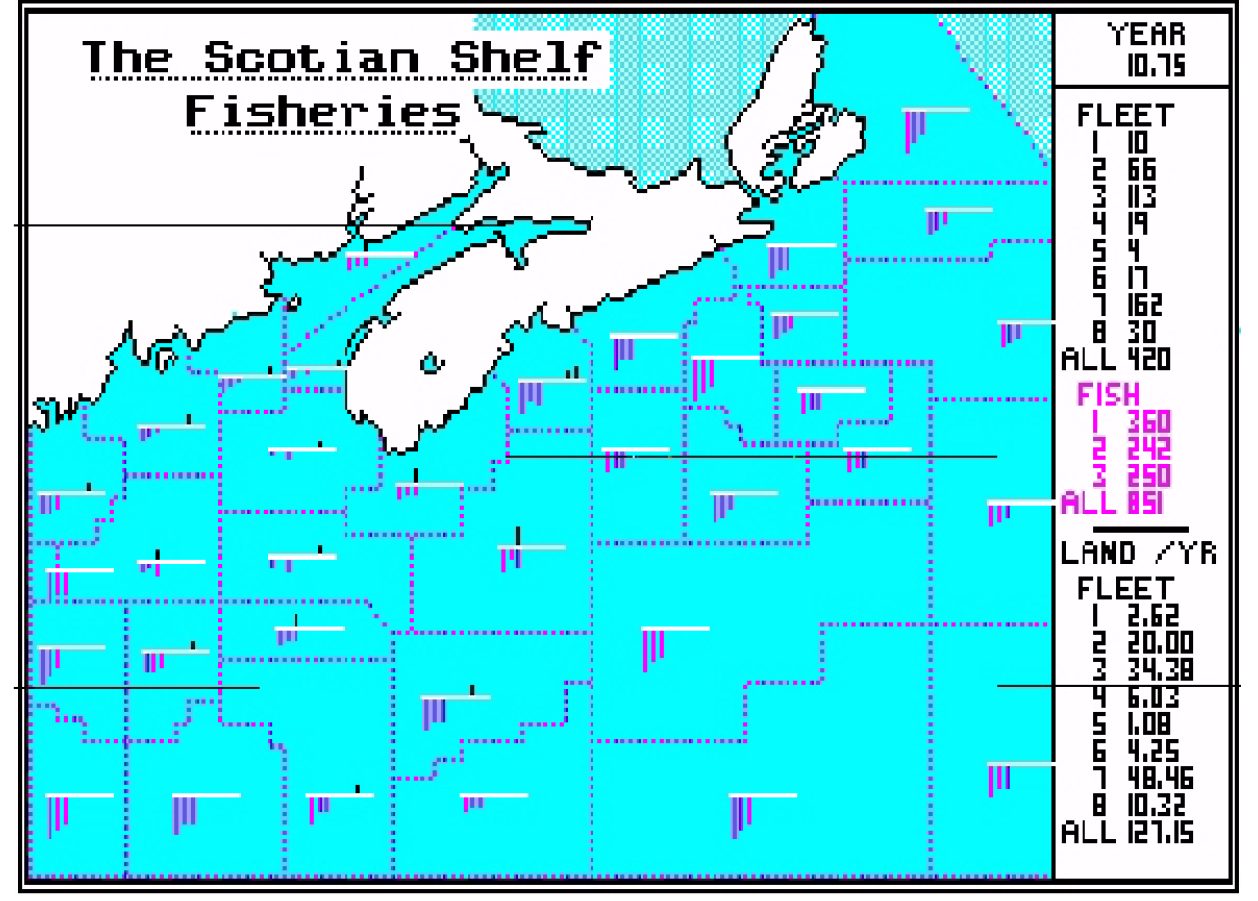
Figure 9 After 30 years fleet 7 has the best strategy (fast response to profit/loss), although previously fleet 2 was best and then fleet 3

The importance of this model is that it demonstrates how, as we relax the assumptions we normally make in order to obtain simple, mechanistic representations of reality, we find that our model can really tell us things we did not know. Our stories become richer and more variable, as different outcomes occur and different lessons are learnt. In the spatial model, we found that economically suboptimal behavior (low R) was necessary in order to fish successfully, and that there was no single “optimal” behavior or strategy, but there were possible sets of compatible strategies. The lesson was that the pattern of fishing effort at any time cannot be “explained” as being optimal in any way, but instead is just one particular moment in an unending, imperfect learning process involving the ocean, the natural ecosystem, and the fishermen.

What is important is even further from the “observed” behavior of the boats and the fish. It concerns the “meta” mechanisms by which the parameter space of possible fishing strategies is explored. By running “learning fleets” with different learning mechanisms in competition with each other, our model can begin to show us which mechanisms succeed in successfully generating and accumulating knowledge of how to succeed, and which do not. Our model has moved from the domain of the physical—mesh size, boat power, trawling versus long lining, etc.—to the nonphysical—How often should I monitor performance? What changes could I explore? How can I change behavior? Which parameters are effective?—in short, how can I learn? This results from relaxing both assumptions 3 and 4. We move from a descriptive mechanical model to an evolving model of learning “inside” fishermen, where behavior and strategies change, and the payoffs and consequences emerge, over time.

DISCUSSION

We have shown that knowledge generation results from making “simplifying” assumptions. If these are all true, we have a truly appropriate and useful model; but if the assumptions do not hold, our model may be completely misleading. Our reflection considered:

These represent successively more general models, each step containing the previous one as a special case, but also of increasing difficulty, and indeed still probably far from “reality.” It is small wonder that most people probably have a very poor understanding of the real consequences of their actions or policies.

The discussion above also brings out a great deal concerning the ideas that underlie the “sustainability” of organizations and institutions. This does not result from finding any fixed, unbeatable set of operations that correspond to the peak of some landscape of fitness. Any such landscape is a reflection of the environment and of the strategies of the other players, and so it never stops changing. Any temporary “winner” will need continually to monitor what is happening, reflect on possible consequences, and possess the mechanisms necessary for self-transformation. This will lead to the simultaneous “sustaining and transformation” of the entities and of the system as new activities, challenges, and qualities emerge. The power to do this lies not in extreme efficiency, nor can it be had necessarily by allowing free markets to operate unhindered. It lies in creativity. And, in turn, this is rooted in diversity, cultural richness, openness, and the will and ability to experiment and to take risks.

Instead of viewing the changes that occur in a complex system as necessarily reflecting progress up some pre-existing (if complex) landscape, we see that the landscape of possible advantage itself is produced by the actors in interaction. The detailed history of the exploration process itself affects the outcome. Paradoxically, our scientific pursuit of knowledge tells us that uncertainty is therefore inevitable, and we must face this. Longterm success is not just about improving performance with respect to the external environment of resources and technology, but also is affected by the “internal game” of a complex society. The “payoff” of any action for an individual cannot be stated in absolute terms, because it depends on what other individuals are doing. Strategies are interdependent.

Ecological organization is what results from evolution, and it is composed of self-consistent “sets” of activities or strategies, both posing and solving the problems and opportunities of their mutual existence. Innovation and change occur because of diversity, nonaverage individuals with their bizarre initiatives, and whenever this leads to an exploration into an area where positive feedback outweighs negative, growth will occur. Value is assigned afterward. It is through this process of “post-hoc explanation” that we rationalize events by pretending that there was some pre-existing “niche” that was revealed by events, although in reality there may have been a million possible niches and one particular one arose.

The future, then, is not contained in the present, since the landscape is fashioned by the explorations of climbers, and adaptability will always be required. This does not necessarily mean that total individual liberty is always best. Our models also show that adaptability is a group or population property. It is the shared experiences of others that can offer much information. Indeed, it pays everyone to help facilitate exploration by sharing the risks in some cooperative way, thus taking some of the “sting” out of failure. There is no doubt that the “invention” of insurance and of limited liability has been a major factor in the development of our economic and social system. Performance is generated by mutual interactions, and total individual freedom may not be consistent with good social interactions, and hence will make some kinds of strategy impossible. Once again, we must differentiate between an “external game,” where total freedom allows wide-ranging responses to outside changes, and an “internal game,” where the division of labor, internal relations, and shared experiences play a role in the survival of the system.

Again, it is naïve to assume that there is any simple “answer.” The world is just not made for simple, extreme explanations. Shades of grey, subjective judgments, postrationalizations, multiple misunderstandings, and biological/emotional motivations are what characterize the real world. Neither total individual freedom nor its opposite are solutions, since there is no “problem” to be solved. They are possible choices among all the others, and each choice gives rise to a different spectrum of possible consequences, different successes and failures, and different strengths and weaknesses. Much of this probably cannot really be known beforehand. We can only do our best to put in place the mechanisms that allow us always to question our “knowledge” and continue exploring. We must try to imagine possible futures, and carry on modifying our views about reality and about what it is that we want.

Mismatches between expectations and real outcome may either cause us to modify our (mis)understanding of the world, or simply leave us perplexed. Evolution in human systems is therefore a continual, imperfect learning process, spurred by the difference between expectation and experience, but rarely providing enough information for a complete understanding.

Instead of the classical view of science eliminating uncertainty, the new scientific paradigm accepts uncertainty as inevitable. Indeed, if this were not the case, then it would mean that things were preordained, which would be much harder to live with. Evolution is not necessarily progress and neither the future nor the past was preordained. Creativity really exists, it is the motor of change, and the hidden dynamic that underlies the rise and fall of civilizations, peoples, and regions, and evolution both encourages and feeds on invention. Recognizing this, the first step toward wisdom is the development and use of mathematical models that capture this truth.

References

Allen, P M. (1985) “Towards a New Science of Complex Systems,” in The Science and Praxis of Complexity, Tokyo: United Nations University Press: 268-97.

Allen, P M. (1988) “Evolution: Why the Whole is Greater than the Sum of its Parts,” in W. Wolff, C.-J. Soeder, & F. R. Drepper (eds) Ecodynamics, Berlin: Springer Verlag: 2-30.

Allen, P M. (1993) “Evolution: Persistent Ignorance from Continual Learning,” in R. H. Day & P Chen (eds) Nonlinear Dynamics and Evolutionary Economics, Oxford, UK: Oxford University Press: 101-12.

Allen, P M. (1994) “Evolutionary Complex Systems: Models of Technology Change,” in L. Leydesdorff & P. van den Besselaar (eds) Chaos and Economic Theory, London: Pinter.

Allen, P. M. (1994) “Coherence, chaos and evolution in the social context,” Futures, 26(6): 583-97.

Allen, P M. (1998) “Evolving Complexity in Social Science,” in G. Altmann & W. A. Koch (eds) Systems: New Paradigms for the Human Sciences, BerlinYork: Walter de Gruyter.

Allen, P M. & McGlade, J. M. (1986) “Dynamics of discovery and exploitation: The Scotian Shelf fisheries,” Canadian Journal of Fisheries and Aquatic Sciences, 43(6): 1187-200.

Allen, P M. & McGlade, J. M. (1987a) “Evolutionary drive: The effect of microscopic diversity, error making and noise,” Foundations of Physics, 17(7, July): 723-38.

Allen, PM. & McGlade, J.M. (1987b) “Modelling Complex Human Systems: A Fisheries Example,” European Journal of Operations Research, 30: 147-67.

Allen, P M. & McGlade, J. M. (1989) “Optimality, Adequacy and the Evolution of Complexity,” in P. L. Christiansen & R. D. Parmentier (eds) Structure, Coherence and Chaos in Dynamical Systems, Manchester, UK: Manchester University Press.

Barucha-Reid, A. T. (1960) Elements of the Theory of Markov Processes and Their Applications, New York: McGraw-Hill.

Eigen, M. & Schuster, P. (1979) The Hypercycle, Berlin: Springer Verlag.

Haken, H. (1977) Synergetics, Heiderlberg, Germany: Springer Verlag.

McGlade, J. M. & Allen, P .M. (1985) “The fishing industry as a complex system,” Canadian Technical Report of Fisheries and Aquatic Sciences, No 1347, Ottawa, Canada: Fisheries and Oceans.

Nicolis, G. & Prigogine, I. (1977) Self-Organization in Non-Equilibrium Systems, New York: Wiley.