Fluctuations and order in ecosystem dynamics
Robert E. Ulanowicz
University of Maryland Center for Environmental Science, USA
Abstract
The model by Prigogine and Nicolis suggesting how microscopic fluctuations can instigate major changes in macroscopic configurations stands as a landmark contribution, helping to incite the current explosion of interest in complex systems. This model restricts causal agency solely to simple, generic microscopic fluctuations and is formulated under assumptions that pertain largely to physical systems. In the realm of ecosystem dynamics, however, where the hierarchical order of attributes is sometimes inverted, it appears unlikely that the order-through-fluctuations scenario can provide a sufficient narrative of change. In particular, mutualistic, macroscopic configurations within ecosystems appear to exert active agency upon their microscopic features.
Ilya Prigogine, prophet of complexity
The world of science is not exempt from the dictates of fashion. Scientific themes often spring into the limelight overnight and burn with a luminous intensity. To an extent, the advent of Complexity Theory happened this way, due in large measure to a very talented set of publicists at the Santa Fe Institute who seemed to have open access to the science and book review pages of the New York Times. Science often gains in public esteem from such meteoric appearances, but in the process the tacit assumption all too often precipitates that the theme in question somehow appeared ex-nihilo, when the larger truth is that the groundwork for such startling advances had been laid decades earlier by individuals who remain relatively unsung as the latest fervor builds.
With this as background, I find it most fitting that the Second Biennial Seminar on Complexity Theory featured the pioneering work of the late Ilya Prigogine, which loomed large in the minds of many early investigators into Complexity. On a personal note, as a graduate student, I was nearly obsessed with Prigogine’s early proposition that processes and elements in thermodynamic systems near-equilibrium would somehow arrange themselves into configurations that would generate entropy at the slowest rate possible (Prigogine, 1945.) The phenomenological idea (not so foreign to thermo-dynamicists) that an attribute of the whole system is deserving of study entirely in abstraction from any of its constituent details was to me an exciting alternative to business-as-usual in systems theory.
Then, at about the time I changed my own professional focus towards ecology, Prigogine and Nicolis began to promote the notion of a ‘dissipative structure’—a configuration of processes that operates far-from-equilibrium, that is open to exchange of material and energy with their surroundings, and which maintains its basic integrity over time (Nicolis & Prigogine, 1977.) This concept received special mention by the Nobel Committee that awarded Prigogine its 1977 Prize in Chemistry, and it provided such a wonderful template for the ecosystems that I was beginning to study.
Suddenly, however, the tenor of Prigogine’s research seemed to shift, as he began to focus on microscopic fluctuations. Nonlinear systems, he and Nicolis argued, can exhibit bifurcated behaviors at certain points along parameter space, and which behavior any particular trajectory would follow was determined by arbitrary microscopic events at the bifurcation point. The model, which became known as order-through-fluctuations (OTF), was brilliantly ex-pounded in a book by Nicolis and Prigogine (1977), and it played a central role in the latter’s widely successful narrative, Order out of chaos with Isabel Stengers (Prigogine & Stengers, 1984.)
I could not help but applaud the elegance of this new model, but at the same time I must confess to a certain feeling of disappointment with the shift in Prigogine’s focus toward the microscopic. I felt that he had lost interest in the role of the macroscopic in development. My intuition was confirmed on one of the few brief occasions when I had the privilege to engage Prigogine in private conversation. I asked him why he seemed to have abandoned his earlier emphasis on macroscopic systems? His answer to me was pointed and decisive—“Because they are trivial! ” With all due and enormous respect for Prigogine and with my sincere acknowledgement of his substantial contributions to my own worldview, I would like to take this opportunity to disagree profoundly with this judgement.
The full story?
Many of the most successful models are characterized by elegant simplicity. Such models not only satisfy Occam’s Razor, but they also promulgate readily because they serve as attractive pedagogical tools. OTF is such a model, but in the face of today’s growing appreciation for the complex in nature, it is well that we should pause to ask exactly how far such physical models can adequately represent the processes comprising living systems? Certainly, like much of what we now encounter under the rubric of Artificial Life, simple models do help to elucidate some of the workings of living systems. They could easily become misleading, however, if one tacitly assumes that they constitute either necessary or sufficient elements of the life process.
Rather than address the mathematics that portray the dynamics of OTF, I choose instead to focus on the generality of its underlying assumptions, some of which remain implicit in most presentations. These postulates are characteristic of much of what today passes for mechanistic explanations of living phenomena, and I worry that the understandable desire for simplicity can all too easily degrade into an unwarranted minimalism (Ulanowicz, 1999.) The narrow aim here is simply to contrast, in conceptual terms, OTF with currently evolving views in ecosystems ecology. Those desiring a more quantitative description of my perspectives on ecosystem development are referred to Ulanowicz and Norden (1991) and Ulanowicz (2004a,b.)
As Albert Einstein once famously opined, “Everything should be made as simple as possible, but not simpler.” In that vein, I note as how the fluctuations which impinge upon any given system are implicitly assumed to be both simple and generic. About the only distinction drawn among the perturbations is their direction—whether they affect the chosen system parameter in one direction or in the other. Suffice it for now to remark that in biology perturbations arise having a wide variety of identifiable forms and patterns, many of which are complex in themselves. The effect of such a perturbation could well depend on its complex nature. For example, a weakened organism might fall easy victim to a certain bacterium, while at the same time remaining robustly indifferent to exposure to a particular virus.
Furthermore, to regard fluctuations as generic is to imply that all tokens are repeatable with arbitrary frequency. Repeatability is necessary to the Baconian pursuit of science, and there is no place whatsoever in ‘normal science’ for events that are unique over all time and space. A small point this, but it should also be noted, that in OTF behaviors are limited to those that are bipartite in nature. In ecology decisions among multiple behaviors are made all the time, as when a predator at a watering hole chooses from a variety of prey available to it at the moment.
Finally, and in my judgement most importantly, OTF accords with conventional scientific postulates in its portrayal of causal agency as originating solely from the microscopic fluctuations and acting upon the macroscopic system, which for its part can only react to the smaller mechanisms but cannot exert any influence upon them.
Normal science
Regarding the allusions that have just been made to ‘conventional’ or ‘normal’ science, it behooves us to be more precise about what that term entails. As Kuhn, (1962) suggested, each individual scientist weights differently the various criteria that are used to delimit legitimate science. To deal with such diversity, I choose to enumerate a set of fundamental postulates that formed a broad consensus about nature around the turn of the Nineteenth Century (ca. 1800.) This ‘strawman’ suite of five assumptions will then serve as a reference against which to compare OTF with our current image of ecosystem dynamics. (In what ensues, no mention is made of either chaos or thermodynamics as they relate to Newtonianism. These relationships are addressed elsewhere in Ulanowicz, 1997.)
According to Depew and Weber (1995), there were four fundamental postulates about nature according to which Newtonian investigations were pursued:
- Newtonian systems are causally closed. Only mechanical or material causes are legitimate.
- Newtonian systems are deterministic. Given precise initial conditions, the future (and past) states of a system can be specified with arbitrary precision.
- Newtonian systems are reversible. Laws governing behavior work the same in both temporal directions.
- Newtonian systems are atomistic. They are strongly decomposable into stable least units, which can be built up and taken apart again. In addition, Prigogine and Stengers (1984, see also Ulanowicz, 1999) alluded to a fifth article of faith, namely that:
- Physical laws are universal. They apply everywhere, at all times and scales.
Against this background, it is immediately obvious that OTF departs from the historical conception of science in its abrogation of determinism and reversibility. Prigogine and Stengers (1984) also contend that OTF challenges the notion of universality. On the other hand, it is rather clear that OTF, with its unidirectional causality contradicts neither closure nor atomism and actually reinforces the former.
Ecosystem dynamics
As soon as one enters the complex realm of ecology, however, it becomes necessary to reevaluate the underlying framework for scientific study. Some conventional relationships actually become inverted. For example, the organizational status of the ‘microscopic’ level in ecology (the organisms) is, in most cases, far more highly organized than the macroscopic ensemble itself (Ulanowicz, 2001.) This turn of affairs forces us to reconsider our assumptions, both (a) about the nature of contingencies and (b) about the dynamics between such fluctuations and the order of the larger ecosystem.
In ecosystems, then, one can no longer assume that ‘fluctuations’ at the microscopic level are simple and generic. One even must entertain the possibility that many events occurring in ecosystems are singular and unique for all time. To see why this is likely, I invoke an argument formulated several decades ago by the physicist Walter Elsasser, (1969). Elsasser sought to delimit what he called an “enormous” number. By this he was referring to numbers so large that they should be excluded from physical consideration, because they greatly exceed the number of physical events that possibly could have occurred at any scale since the Big Bang. To provide an estimate of the threshold for enormous numbers Elsasser reckoned the number of simple protons in the known universe to be about 1085. He then noted as how the number of nanoseconds that have transpired since the beginning of the universe is about 1025. Hence, his rough estimate of the upper limit on the number of conceivable events that could have occurred in the physical world is about 10110. Any number of possibilities much larger than this value simply loses any meaning with respect to physical reality.
Anyone familiar with combinatorics immediately will realize that it doesn’t take very many identifiable elements or processes before the number of their possible configurations becomes enormous. One doesn’t need Avagadro’s Number of particles (1023) to produce combinations in excess of 10110—a system with merely 80 or so distinguishable components will suffice. In probabilistic terms, any event randomly comprised of more than 80 separate elements is almost certain never have occurred earlier in the history of the universe. Such a constellation is unique once and for all time. It follows, then, that in ecosystems with hundreds or thousands of distinguishable organisms, one must reckon not just with occasional unique events, but with a legion of them. Unique, singular events are occurring all the time, everywhere and at all scales! In the face of this reality, all talk of determinism as a universal characteristic is futile (Popper, 1990). Still, although such noise cannot be accommodated by Baconian science, a degree of regularity can be recognized in some ecological phenomena, such as succession. How then does such order arise, and what maintains it?
I wish to suggest that the key to how living systems act differently from purely physical systems has to do with positive feedback. Of course, narratives abound describing the roles that positive feedbacks play in the dynamics of living systems (e.g., Eigen, 1971; Maturano & Varela, 1980; DeAngelis, et al., 1986; Haken, 1988; Kauffman, 1995.) My focus here will be on the dynamics of autocatalytic cycles (Ulanowicz, 1997), and in this essay autocatalysis will be considered any manifestation of a positive feedback loop whereby the direct effect of every link on its downstream neighbor is positive. Without loss of generality, let us focus our attention on a serial, circular conjunction of three processes -A, B, and C (see Figure 1) Any increase in A is likely to induce a corresponding increase in B, which in turn elicits an increase in C, and whence back to A.
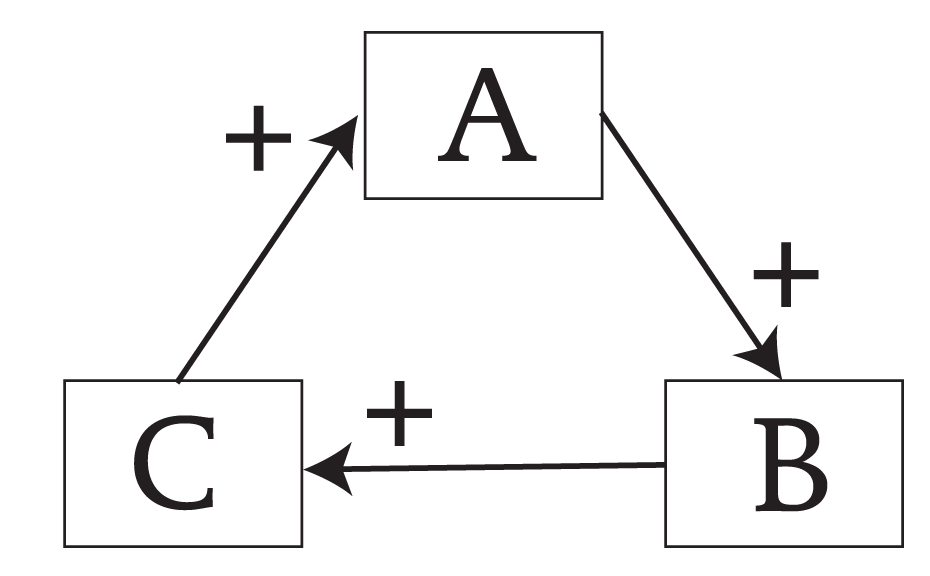
Figure 1 A simple example of autocatalysis
A didactic example of autocatalysis in ecology is the community that builds around the aquatic macrophyte, Utricularia (Ulanowicz, 1995). All members of the genus Utricularia are carnivorous plants. Scattered along its feather-like stems and leaves are small bladders, called ‘utricles’ (see Figure 2a). Each utricle has a few hair-like triggers at its terminal end, which, when touched by a feeding zooplankter, opens the end of the bladder, and the animal is sucked into the utricle by a negative osmotic pressure that the plant had maintained inside the bladder. In nature the surface of Utricularia plants is always host to a film of algal growth known as periphyton. This periphyton in turn serves as food for any number of species of small Zooplankton. The autocatalytic cycle is closed when the Utricularia captures and absorbs many of the Zooplankton (see Figure 2b).
In chemistry, where reactants are simple and fixed, autocatalysis behaves just like any other mechanism. As soon as one must contend with organic macromolecules and their ability to undergo small, incremental alterations, however, the game changes. Especially when the effect of any catalyst on the downstream element is fraught with contingencies (rather than being obligatory), a number of decidedly non-mechanical behaviors can arise (Ulanowicz, 1997). For the sake of brevity, I will discuss only a few.
Perhaps most importantly, autocatalysis is capable of exerting selection pressure upon its ever- changing, malleable constituents. To see this, one considers a small spontaneous change in process B. If that change either makes B more sensitive to A or a more effective catalyst of C, then the transition will receive enhanced stimulus from A. Conversely, if the change in B either makes it either less sensitive to the effects of A or a weaker catalyst of C, then that perturbation will likely receive diminished support from A. That is to say that there is a preferred direction inherent in autocatalysis—that of increasing autocatalytic participation. This preferred direction can be interpreted as a breaking of symmetry. Such asymmetry has been recognized in physics since the mid-1960s and it transcends the assumption of reversibility. Furthermore, with such increasing autocatalytic engagement, or mutual adaptation, elements lose their capability of acting on their own; or, should they remain capable of persisting in isolation, it would be with behavior radically different from that exhibited as part of the autocatalytic scheme. That is, the full cycle manifests an organic nature that is refractory to the assumption of atomism.

Figure 2 (a) Utricularia, a carnivorous plant (b) The cycle of rewards in the Utricularia system.
To see how another very important attribute of living systems can arise, one notes in particular that any change in B is likely to involve a change in the amounts of material and energy that are required to sustain process B. As a corollary to selection pressure, we immediately recognize the tendency to reward and support any changes that serve to bring ever more resources into B. Because this circumstance pertains to any and all members of the feedback loop, any autocatalytic cycle becomes the epi-center of a centripetal flow of resources towards which as many resources as possible will converge (see Figure 3). That is, an autocatalytic loop defines itself as the focus of centripetal flows. Bertrand Russell, (1960) identified such “chemical imperialism” as the very crux of evolutionary drive.
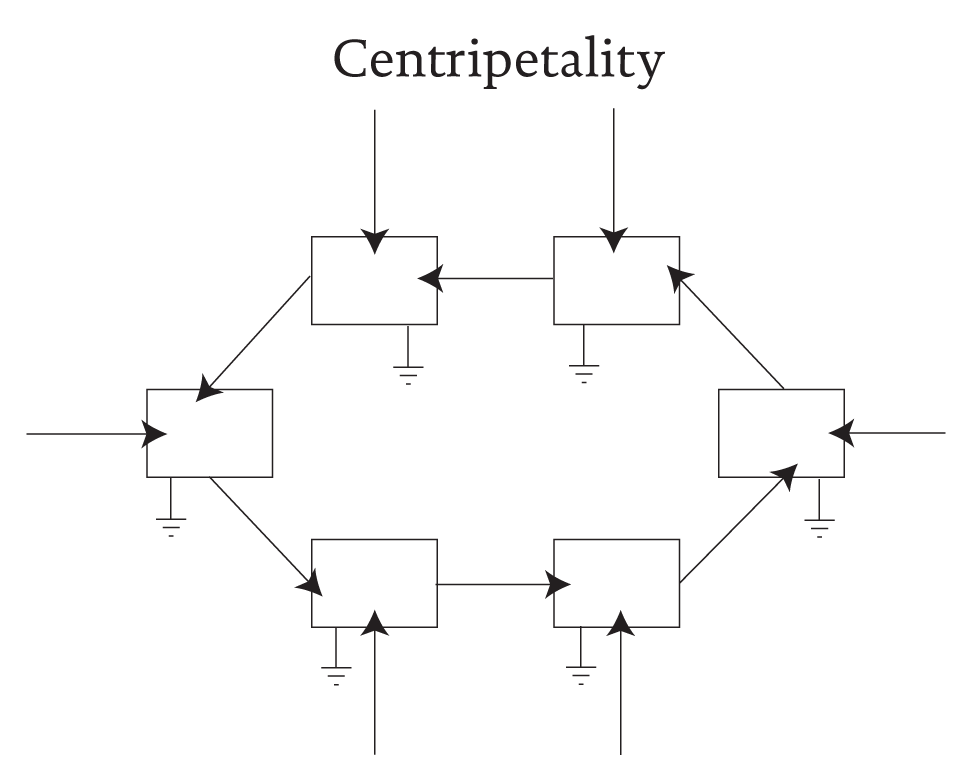
Figure 3 Centripetal action as engendered by autocatalysis
Autocatalytic selection pressure, then, is exerted in top-down fashion—contingent action by the macroscopic ensemble upon its constituent elements. Furthermore, centripetality is best identified as an agency acting at the focal level. Both of these modes of action violate the restriction of causal closure, which permits only mechanical actions at smaller levels to elicit changes at higher scales. Complexity, therefore, can be more than the ramification of simple events occurring at smaller scales.
Centripetality in its turn guarantees that whenever two or more autocatalytic loops exist in the same system and draw from the same pool of finite resources, competition among the foci will necessarily ensue. In particular, whenever two loops share pathway segments in common, the result of this competition is likely to be the exclusion or radical diminution of one of the non-overlapping sections.
For example, should a new element D happen to appear and to connect with A and C in parallel to their connections with B, then if D is more sensitive to A and/or a better catalyst of C, the ensuing dynamics should favor D over B to the extent that B will either fade into the background or disappear altogether (see Figure 4). That is, the selection pressure and centripetality generated by complex autocatalysis (a macroscopic ensemble) is capable of influencing the replacement of elements.

Figure 4 The selection of new element D to replace B.
In addition to selection and centripetality, another new perspective afforded by ecodynamics is the possibility that agency can be exerted by a configuration of processes. An autocatalytic loop is such a configuration, and we have just noted how the selection generated by autocatalysis can strongly influence which objects remain and which pass from the scene. Unlike the conventional attitude that all events are the consequences of actions by objects, it is now entirely conceivable that objects themselves can be the outcomes of the agency inherent in configurations of processes. This new angle reinforces Prigogine’s suggestion that we should begin to shift our focus on nature away from being and toward becoming (Prigogine, 1980).
Finally, it is worthwhile to note how auto- catalytic selection can act to stabilize and regularize behaviors across the hierarchy of scales. Unlike with Newtonian universality, a chance happening anywhere rarely will ramify up and down the hierarchy without attenuation. The effects of noise at one level are usually subject to autocatalytic selection at higher levels and to energetic culling at lower levels. Nature as a whole exhibits regularities, but in place of the universal effectiveness of all natural laws, we discern instead a granularity inherent in the real world. That is, models of events at any one scale can explain matters at another scale only in inverse proportion to the remoteness between them. Obversely, the domain within which irregularities and perturbations can damage a system is usually circumscribed. Chance does not necessarily unravel a system.
A new metaphysic
The reader who has been counting violations will now recognize that the topsy-turvy world of ecology appears to stand all the fundamental assumptions of normal science on their heads. Instead of a world that is closed, atomistic, reversible, deterministic and universal; we now see one that is (respectively) open, organic, historical, contingent and granular. I submit that there remains little hope that mechanical models, even sophisticated ones like OTF, will prove sufficient under this new perspective. All of which is not to deny that we can gain insights into particular aspects of living systems through mechanical models, as is the goal of the burgeoning field called Artificial Life. It does warn us, however, that we must exercise the utmost caution in extrapolating some of the intriguing results from mechanical models into the actual w chaos’, actual data fail to support such projections (Ulanowicz, 1997; Zorach & Ulanowicz, 2003).
Furthermore, it is widely appreciated that mechanical models are ill-suited to the study of emergence, because true novelty by definition remains beyond the scope of closed systems. Emergence remains an enigma to the mechanical world-view, because all behaviors of mechanical models were built into their specifications, either explicitly or inadvertently. Recognizing the existence of sin-gular events, however, breaks with the continuum assumption, and the selection by autocatalysis from among such intrinsic novelties provides a very natural pathway for true changes to emerge.
Finally, with respect to OTF, I retain a strong appreciation for how this model explicates a certain subclass of transitions within (mostly physical) self-organizing systems. As a sufficient model for developing biological systems, however, I believe that OTF misleads us when it attributes all agency to microscopic fluctuations. Most certainly, microscopic noise is necessary for development, but we must never lose sight of the counterpoint that macroscopic configurations play every bit as active a role in the scenario of development—and possibly even the greater one. They most decidedly are not trivial!
Acknowledgments
The author was supported in part during the writing of this brief essay by the National Science Foundation’s Program on Biocomplexity (Contract No. DEB-9981328.) He also wishes to express his gratitude to Dr. Pedro Sotolongo for inviting him to participate in the Prigogine Forum at the Second Biennial International Seminar on the Philosophical, Epistemological and Methodological Implications of Complexity Theory held January, 2004 in La Habana, Cuba. An anonymous reviewer helped to uncover certain deficiencies in the original manuscript.
References
DeAngelis, D. L., Post, W. M., Travis, C. C . (1986). Positive feedback in natural systems, New York, NY: SpringerVerlag, ISBN 0387159428.
Depew, D. J. and Weber, B. H. (1995). Darwinism evolving: Systems dynamics and the geneology of natural selection, Cambridge, MA: MIT Press, ISBN 0262540835 (1996).
Eigen, M. (1971). “Self-organization of matter and the evolution of biological macromolecules,” Naturwissenschaften, ISSN 0028-1042, 58: 465523.
Elsasser, W. M. (1969). “Acausal phenomena in physics and biology: A case for reconstruction,” American Scientist, ISSN 0003-0996, 57(4): 502-516.
Haken, H. (1988). Information and self-organization, Berlin: Springer-Verlag, ISBN 3540662863 (2000).
Kauffman, S. (1995). At home in the universe: The search for the laws of self organization and complexity, New York, NY: Oxford University Press, ISBN 0195111303 (1996).
Kuhn, T. S. (1962). The structure of scientific revolutions, Chicago: University of Chicago Press, ISBN 0226458083 (1996).
Maturana, H. R. and Varela, F. J. (1980). Autopoiesis and cognition: The realization of the living, Dordrecht: D. Reidel, ISBN 9027710163 (1991).
Nicolis, G. and Prigogine, I. (1977). Self-organization in nonequilibrium systems: From dissipative structures to order through fluctuations, New York , NY: Wiley, ISBN 0471024015.
Popper, K. R. (1990). A world of propensities, Bristol, UK: Thoemmes, ISBN 1855060000 (1997).
Prigogine, I. (1945). “Moderation et transformations irreversibles des systemes ouverts,” Bull. Cl. Sci. Acad. R. Belg. Cinque E Ser., 31: 600-606.
Prigogine, I. (1980). From being to becoming: Time and complexity in the physical sciences, San Francisco, CA: W. H. Freeman, ISBN 0716711087 (1981).
Prigogine, I. and Stengers, I. (1984). Order out of chaos: Man’s new dialogue with nature, New York, NY: Bantam, ISBN 0553343637.
Russell, B. (1960). An outline of philosophy, Cleveland, OH: Meridian Books, ISBN 004192035X (1979).
Ulanowicz, R. E. (1995). “Utricularia’s secret: The advantages of positive feedback in oligotrophic environments,” Ecological Modeling, ISSN 0304-3800, 79: 49-57.
Ulanowicz, R. E. (1997). Ecology: The ascendant perspective, New York, NY: Columbia University Press, ISBN 023110829X.
Ulanowicz, R. E. (1999). “Life after Newton: An ecological metaphysic,” BioSystems, ISSN 0303-2647, 50: 127142.
Ulanowicz, R. E. (2001). “The organic in ecology,” Ludus Vitalis, ISSN 1133-5165, 9(15): 183-204.
Ulanowicz, R. E. (2004a). “On the nature of ecodynamics,” Ecological Complexity, ISSN 1476-945X, 1: 341354.
Ulanowicz, R. E. (2004b). “Quantitative methods for ecological network analysis,” Computational Biology and Chemistry, ISSN 1476-9271, 28: 321-339.
Ulanowicz, R. E. and Norden, J. S. (1990). “Symmetrical overhead in flow networks,” International Journal of Systems Science, ISSN 0020-7721, 1: 429-437.
Zorach, A. C. and Ulanowicz, R. E. (2003). “Quantifying the complexity of flow networks: How many roles are there?” Complexity, ISSN 1076-2787, 8(3):68-76.